算法理论
创建两个数组-d数组以及p数组
d数组存放顶点间的最短距离,p数组存放被指向顶点的前驱
图示
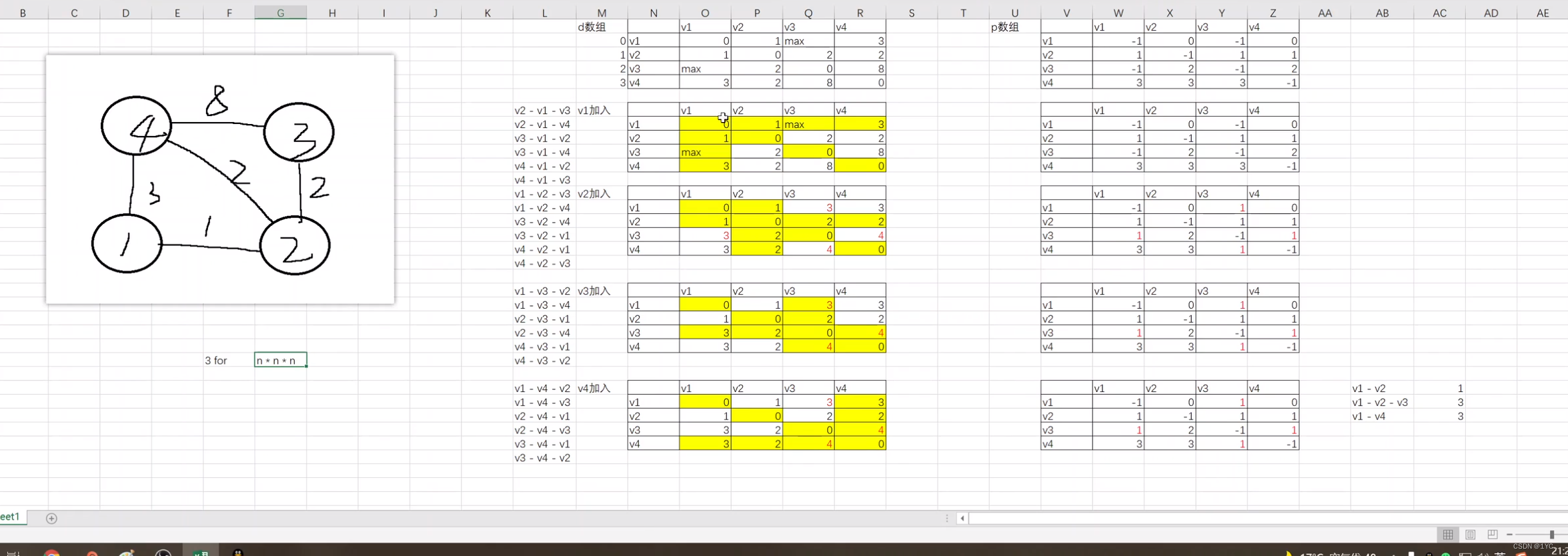 图来自tyrantlucifer@gmail.com
图来自tyrantlucifer@gmail.com
我们通过将每个顶点作为中转点判断以此顶点中转后是否会让两个顶点间的路径更短
如果能,则改变d,p数组中对应的值,
举例
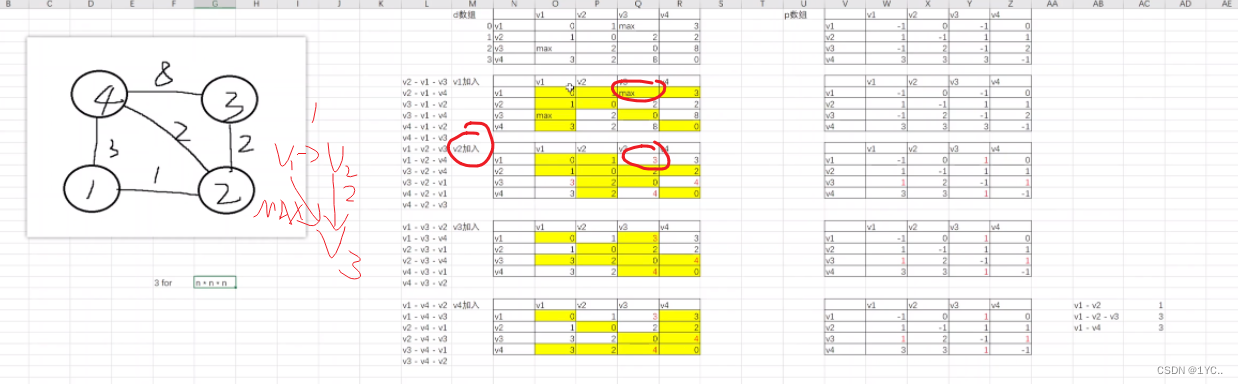
在加入V2作为中转点时,我们发现V1->V3本为不可达,但通过V2中转,路径比原来的短,我们则更改d数组和p数组的值
Floyd算法也被称为3for,
代码实现
接口
#include<stdio.h>
#include <stdlib.h>
#define MAX 32767
#define num 5
typedef struct Graph
{
int vexNum;
int arcNum;
char* vexs;
int** arcs;
}Graph;
Graph* initGraph(int vexNum) ;
void createGraph(Graph* G, char* vexs, int* arcs);
void DFS(Graph* G, int* visited, int index) ;
void floyd(Graph* G);
接口实现
Graph* initGraph(int vexNum) {
Graph* G = (Graph*)malloc(sizeof(Graph));
G->vexs = (char*)malloc(sizeof(char) * vexNum);
G->arcs = (int**)malloc(sizeof(int*) * vexNum);
for (int i = 0; i < vexNum; i++) {
G->arcs[i] = (int*)malloc(sizeof(int) * vexNum);
}
G->vexNum = vexNum;
G->arcNum = 0;
return G;
}
void createGraph(Graph* G, char* vexs, int* arcs) {
for (int i = 0; i < G->vexNum; i++) {
G->vexs[i] = vexs[i];
for (int j = 0; j < G->vexNum; j++) {
G->arcs[i][j] = *(arcs + i * G->vexNum + j);
if (!G->arcs[i][j] && G->arcs[i][j] != MAX) {
G->arcNum++;
}
}
}
G->arcNum /= 2;
}
void DFS(Graph* G, int* visited, int index) {
printf("%c\t", G->vexs[index]);
visited[index] = 1;
for (int i = 0; i < G->vexNum; i++) {
if (G->arcs[index][i] > 0 && G->arcs[index][i] != MAX && !visited[i]) {
DFS(G, visited, i);
}
}
}
void floyd(Graph* G) {
int d[num][num];
int p[num][num];
//初始化两个数组
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
d[i][j] = G->arcs[i][j];
if (G->arcs[i][j] > 0 && G->arcs[i][j] != MAX) {
p[i][j] = i;
}
else {
p[i][j] = -1;
}
}
}
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
printf("%d ", d[i][j]);
}
printf("\n");
}
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
printf("%d ", p[i][j]);
}
printf("\n");
}
//算法执行
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
for (int k = 0; k < G->vexNum; k++) {
//以i为中转点
if (d[j][i] + d[i][k] < d[j][k]) {
d[j][k] = d[j][i] + d[i][k];
p[j][k] = p[i][k];//改变前驱
}
}
}
}
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
printf("%d ", d[i][j]);
}
printf("\n");
}
for (int i = 0; i < G->vexNum; i++) {
for (int j = 0; j < G->vexNum; j++) {
printf("%d ", p[i][j]);
}
printf("\n");
}
}
测试
void text() {
Graph* G = initGraph(4);
int* visited = (int*)malloc(sizeof(int) * G->vexNum);
for (int i = 0; i < G->vexNum; i++)
visited[i] = 0;
int arcs[4][4] = {
0, 1, MAX, 3,
1, 0, 2, 2,
MAX, 2, 0, 8,
3, 2, 8, 0
};
char str[5] = "1234";
createGraph(G, str, (int*)arcs);
DFS(G, visited, 0);
printf("\n");
floyd(G);
}
int main()
{
text();
return 0;
}
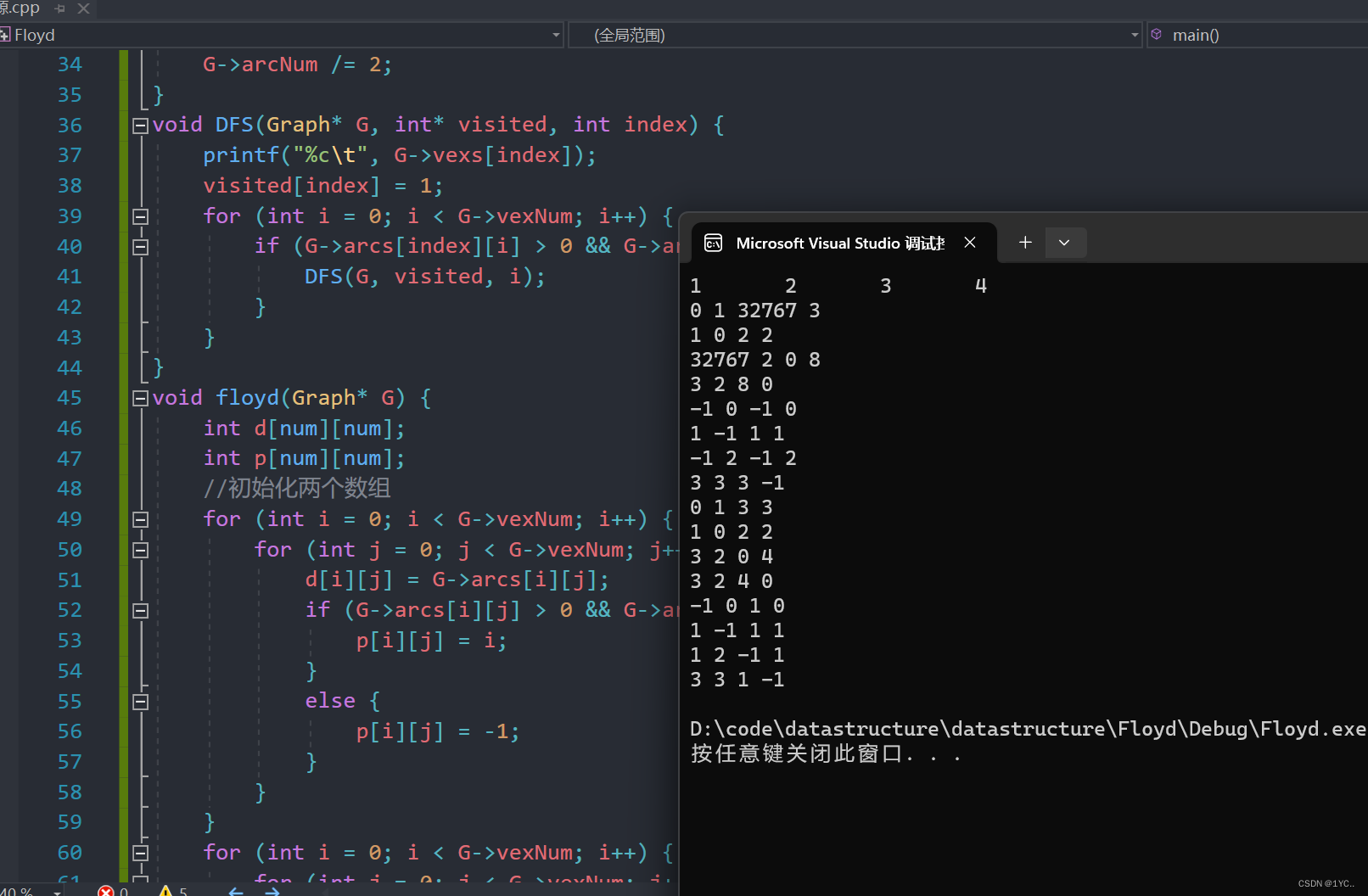







 本文介绍了Floyd算法,用于计算图中任意两个顶点之间的最短路径,通过迭代更新数组来查找可能的中转点,优化路径长度。代码实现了从初始化到执行过程的完整流程。
本文介绍了Floyd算法,用于计算图中任意两个顶点之间的最短路径,通过迭代更新数组来查找可能的中转点,优化路径长度。代码实现了从初始化到执行过程的完整流程。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










