探索递归算法的整个执行过程

一 概述

递归算法是计算机中通过重复将问题分解为同类的子问题而解决问题的方法。递归方式可以被用于解决很多的计算机问题，因此它是计算机科学中十分重要的一个概念。绝大多数编程语言支持函数的自调用，在这些语言中函数可以通过调用自身进行递归。计算机理论可以证明递归的作用可以完全取代循环，因此在很多的函数编程语言中习惯用递归实现循环。

二 递归算法的整个执行过程的分析

此处借助二叉树的先序遍历递归算法来分析递归算法的整个执行过程

如图：

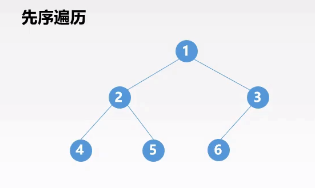
先序遍历二叉树的整个过程为：先遍历根结点，然后遍历左子树，最后遍历右子树。

/**
 *访问根结点
 *先序遍历左子树
 *先序遍历右子树
 */
void PreOrder(BiTree T) {
    if(T!=NULL){
        visit(T);           //访问根结点
        PreOrder(T->lchild);//1.递归遍历左子树
        PreOrder(T->rchild);//2.递归遍历右子树
    }
}

当先序遍历该树时，先将根结点1传入方法PreOrder(BiTree T)，此时函数中的T就代表着根结点1的树，此时就需要执行先序遍历。

对左子树进行访问。

此时应该访问的为根结点为2的左子树，此时的T为根结点为2的左子树，然后继续对其左子树进行访问，执行如下语句：

PreOrder(T->lchild);//1.递归遍历左子树

此时应该访问的为根结点为4的左子树，此时的T为根结点为4的左子树，当这是后继续对其左子树进行访问，执行如下语句：

PreOrder(T->lchild);//1.递归遍历左子树

此时继续访问左子树时，发现以4为根结点的左子树中不存在左子树，所以此时的T为NULL，所以会结束函数PreOrder的执行。

在左子树访问完后，就开始访问右子树。

PreOrder(T->rchild);//2.递归遍历右子树

由树结构可知，访问以4为根结点的右子树为NULL，所以会直接结束函数PreOrder的执行，并进行返回。

此时对以2为根结点的非空右子树进行访问，也就是以5为根结点的右子树。然后对该右子树的左子树进行访问，为NULL则返回，接着对该右子树的左子树进行访问，为NULL则返回。此时对结点5的访问已经结束了。同时对结点2的整个访问过程也结束了。

同理，其他结点也是按照先根，后左，再右的方式进行递归访问，直至结点为NULL则返回。

最后，该树的先序遍历的顺序为：1 2 4 5 3 6