三维环境下的比例导引制导，matlab程序，目标S型机动，附下载链接

在这里插入图片描述

比例导引是导弹制导的方法之一。所谓比例导引法是指导弹在向目标接近的过程中，使导弹的速度向量V在空间的转动角速度正比于目标视线的转动角速度。

文章目录

代码简介
- 主要功能
- 使用说明
运行结果
- 轨迹图
- 捕获时间输出
源代码
参考链接

代码简介

这段MATLAB代码实现了三维空间中的比例导引算法，旨在模拟一个跟踪器对移动目标的追踪过程。代码通过动态计算和更新跟踪器的位置，使其能够有效地接近指定目标。

主要功能

初始化：
- 设置时间步长（tt）和比例缩放因子（sm 和 st）以控制跟踪器与目标之间的动态关系。
- 初始化目标的位置和速度信息。
状态转移矩阵：
- 使用状态转移矩阵（F）描述目标的位置和速度变化，模拟目标的运动轨迹。
主循环：
- 在每个时间步内，更新目标位置，根据设定的S型轨迹，计算当前位置与目标位置之间的距离。
- 计算与目标位置相关的角度和变化量，并在每个时间步更新跟踪器的角度、角速度和位置。
- 通过三角函数和几何关系，确保跟踪器朝着目标移动。
结束条件：
- 当跟踪器与目标之间的距离小于设定阈值时，循环将终止，表示成功追踪目标。
结果可视化：
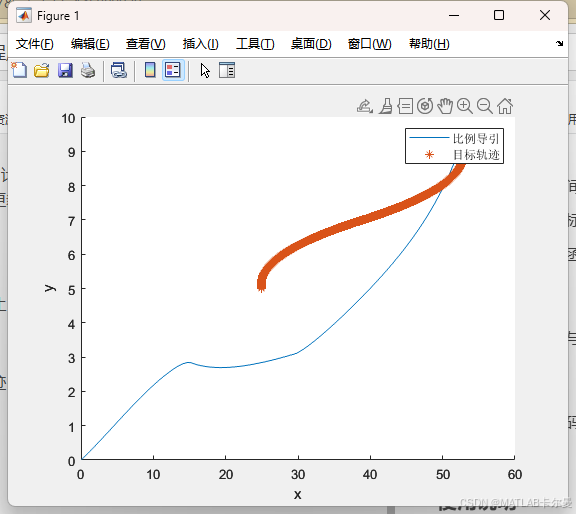
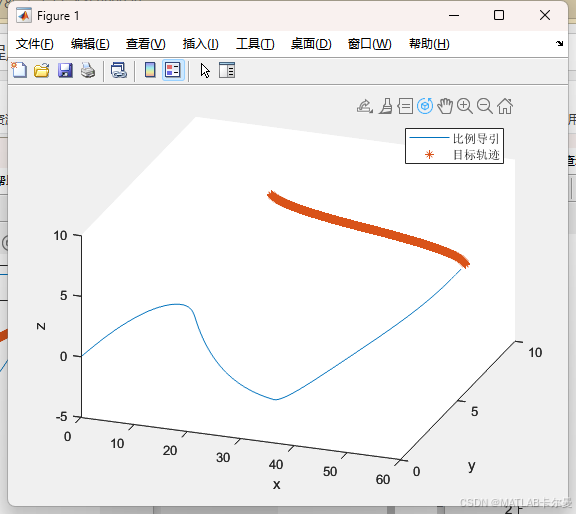
- 最后，代码通过三维图形展示了跟踪器和目标的运动轨迹，使得用户可以直观地观察到比例导引的效果。

使用说明

用户可以通过调整时间步长和比例因子来观察不同参数对跟踪效果的影响。
代码中包含详细的注释，便于理解每一步的实现逻辑和算法原理。

运行结果

轨迹图

在这里插入图片描述
可旋转至三维：

捕获时间输出

命令行输出捕获时间：
在这里插入图片描述

源代码

部分源代码如下：

% 比例导引，三维
% 2025-03-04/Ver1

close all  % 清除工作空间中的所有变量
clc        % 清除命令窗口
clear      % 再次清除工作空间，确保干净状态

% 设置时间步长和模型参数
tt = 0.1;  % 时间步长
sm = 0.6 * tt;  % 跟踪器与目标的比例缩放因子
st = 0.42 * tt; % 目标运动的比例缩放因子

% 初始化当前位置
x(1) = 0;  % 初始x坐标
y(1) = 0;  % 初始y坐标
z(1) = 0;  % 初始z坐标
pmr(:, 1) = [x(1); y(1); z(1)];  % 初始位置数组
ptr(:, 1) = [25; 5; 10;-0.05;0.05;-0.1];  % 目标位置、速度数组
% ptr(:, 1) = [25; 5; 10];  % 目标位置、速度数组

m = 3;  % 比例导引的参数
q(1) = 0;  % 初始角度
o(1) = 0;  % 初始角速度
a(1) = 0;  % 初始角加速度