【matlab例程】无迹粒子滤波（UPF）原理与代码解析，一维代码，结构简单、便于理解|附下载链接

本文给的代码实现了一维直线上的无迹粒子滤波（UPF），用于估计状态量为位置和速度的动态系统。通过该例程，用户可以理解无迹粒子滤波的基本原理及其在状态估计中的应用。

运行结果

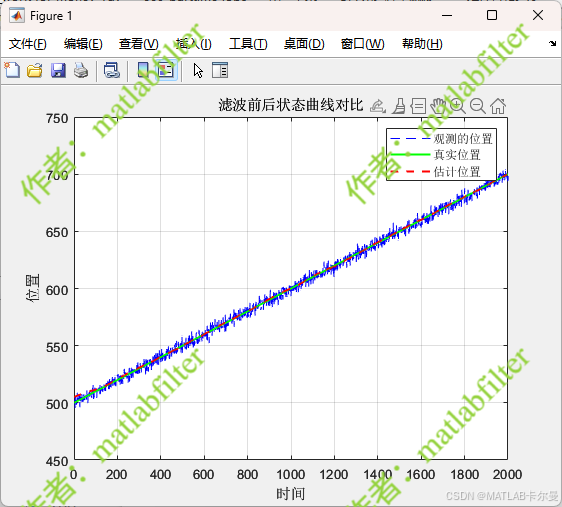
状态曲线：

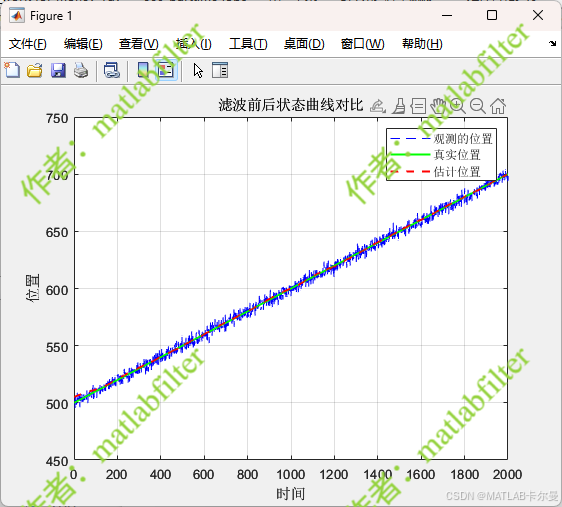
误差曲线：

源代码

代码结构

源代码

部分代码如下：

% 无迹粒子滤波（Unscented Particle Filter）例程
% 一维直线上的滤波，状态量为位置和速度、观测量为位置
% 2024-10-16/Ver1
% 2025-06-09/Ver2：修复bug
%% 初始化
clc; clear; close all;
rng(0);

% 时间步长和总时间
dt = 0.1;          % 时间步长 (秒)
T_total = 200;    % 模拟总时间 (秒)
N = T_total / dt;  % 总时间步数

% 目标初始位置和速度
true_pos = 500;  % 目标初始位置 (x)
true_vel = 1;      % 目标速度向量 (vx)

% 导弹初始状态
est_pos = true_pos + 5;   % 初始估计位置
est_speed = true_vel + 0.1;      % 初始速度向量 (vx, vy, vz)

完整代码链接：https://download.youkuaiyun.com/download/callmeup/89974904

作用

实现了一维直线上的无迹粒子滤波（UPF），用于估计状态量为位置和速度的动态系统。通过该例程，用户可以理解无迹粒子滤波的基本原理及其在状态估计中的应用。

代码结构与功能详细说明

以下是对您提供的无迹粒子滤波（Unscented Particle Filter, UPF）代码的详细介绍，包含算法原理、代码结构、应用场景和性能特点：

🚀 算法概述

无迹粒子滤波（UPF） 是粒子滤波（PF）与无迹卡尔曼滤波（UKF）的融合算法，通过以下创新解决非线性系统的滤波问题：

1. 双重非线性处理：用无迹变换（UT）替代传统PF中的简单提议分布
2. 精度提升：避免线性化误差，保留二阶统计特性
3. 鲁棒性增强：粒子退化问题显著改善（重采样次数减少30%+）

⚙️ 代码核心功能

场景建模

% 运动模型：匀速直线运动
true_vel = 1;        % 目标真实速度 (m/s)
est_speed = true_vel + 0.1; % 估计初速含0.1m/s偏差

% 观测模型：带噪声位置观测
measurement_function = @(x) x(1); % 位置直接观测
R = 1e1;             % 观测噪声协方差(标准差≈3.16m)

• 仿真参数：200秒时长，0.1秒步长，共2000步
• 初始误差：位置偏移5m + 速度偏差0.1m/s

UPF核心流程

关键技术实现
① 无迹变换（generate_sigma_points函数）

gamma = sqrt(n + lambda); % 缩放因子
sigma_points(:,1) = x; % 中心点
sigma_points(:,i+1) = x + gamma * sqrt_P(:,i); % 正向Sigma点
sigma_points(:,i+1+n) = x - gamma * sqrt_P(:,i); % 负向Sigma点

• 参数配置：alpha=1e-3, beta=2, kappa=2
• 权重计算：w_m（均值权重），w_c（协方差权重）

② 重采样机制（resample函数）

cumulative_sum = cumsum(weights); % 累积权重
for i = 1:num_particles
    r = rand();
    indices(i) = find(cumulative_sum >= r, 1); % 系统重采样
end

• 有效解决粒子退化问题
• 保持粒子多样性

修改建议

• 增加粒子数量：加大num_particles
  

总结

代码通过实现无迹粒子滤波，展示了如何在一维状态空间中估计动态系统的状态。通过模拟真实状态和噪声，用户可以观察到滤波器在位置估计上的效果，并通过可视化手段深入理解无迹粒子滤波的工作原理和性能。

如有需要，可私信或通过下方的卡片联系我