hdu 5017 Ellipsoid（西安网络赛 1011）

Ellipsoid

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 850    Accepted Submission(s): 271
Special Judge

Problem Description

Given a 3-dimension ellipsoid(椭球面)

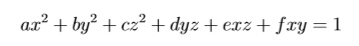
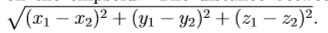
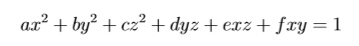
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x ₁,y ₁,z ₁) and (x ₂,y ₂,z ₂) is defined as 

 

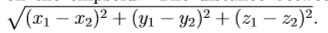
Input

There are multiple test cases. Please process till EOF.

For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f (0 ≤ d,e,f < 1), as described above.  It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.

 

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10 ^-5.

 

Sample Input

  
  

   
   1 0.04 0.01 0 0 0
  
  

 

Sample Output

  
  

   
   1.0000000
  
  

 

第一次了解模拟退火。

求z时已知x，y转化为关于z的二次方程，用韦达定理求z。

关于退火速度，测了一下，r=0.99时是281ms，r=0.98时是140ms，r=0.97时是93ms，r=0.96时就wa了。

代码：、

//97ms
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int dx[8]={0,0,1,-1,1,-1,1,-1};
const int dy[8]={1,-1,0,0,-1,1,1,-1};
const double r=0.97;
const double eps=1e-8;
double a,b,c,d,e,f;
double dis(double x,double y,double z)
{
    return sqrt(x*x+y*y+z*z);
}
double getz(double x,double y)//求z
{
    double A=c;
    double B=d*y+e*x;
    double C=f*x*y+a*x*x+b*y*y-1;
    double delta=B*B-4*A*C;
    if(delta<0)
    {
        return 1e30;
    }
    else
    {
        double z1=(-B+sqrt(delta))/A/2;
        double z2=(-B-sqrt(delta))/A/2;
        return z1*z1<z2*z2?z1:z2;
    }
}
double anneal()//退火
{
    double step=1;
    double x=0,y=0,z;
    while(step>eps)
    {
        z=getz(x,y);
        for(int i=0;i<8;i++)
        {
            double xi=x+dx[i]*step;
            double yi=y+dy[i]*step;
            double zi=getz(xi,yi);
            if(zi>1e20)
            continue;
            if(dis(xi,yi,zi)<dis(x,y,z))
            {
                x=xi;
                y=yi;
                z=zi;
            }
        }
        step=step*r;
    }
    return dis(x,y,z);
}
int main()
{
    while(~scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f))
    {
       printf("%.8f\n",anneal());
    }
    return 0;
}