鱼塘放水

题面
Description

问题描述

庆庆的伯伯承包一个大鱼塘，为了可以放养不同的鱼，鱼塘被分割成N行M列，共有N*M个独立的小池子。各小池子都有独立的进水管，根据放养的鱼种类的不同，控制各小池子的水位。

相邻的小池子之间都有涵洞想通，涵洞配有水闸，水闸平时都是关闭的。只有到换水的时候，才打开某些水闸（涵洞口还有栅栏，你不用担心鱼儿逃跑啦），然后从其中一个小池子（一般都是旁边的小池子）抽水，就可以将整个鱼塘的水换掉。

打开某一个水闸的代价同这个水闸两侧的水位差相一致。在放水前，可以在电控设备上设置好需要打开哪些闸门，按下启动按钮后，同一时间开启需要打开的水闸。

已知各小池子的水位，庆庆想知道开启水闸，开始换水的最小代价，请你帮助他。

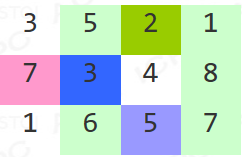
输入格式

第1行，两个数，表示N和M。

以下N行，每行M个整数X，表示各小池子的水位。

输出格式

一个整数，表示开启水闸换水的最小代价。

输入样例

3 4

3 5 2 1

7 3 4 8

1 6 5 7

输出样例

22

数据范围

0<N,M <=100

0<=X<=100

题目分析
粗略理解，就是求最小的连通图

但是到了这里，构图却是一个问题，如何转换呢？

根据题目里说，放一次水的代价是与其相邻的一个池塘的水位的差值，但是在中间部分的话，就会有4个方向，问题会变得十分复杂
我们可以直接转换，把上下面的，和左右面的分开来处理将复杂简单化，处理方式也就是由左到右，由上到下处理

按上面的流程后，我们会得到一个n*m个边的，同时我们要给其起点和终点做定义——是按当前点的个数的
对最小联通图，我们以kruskal来应对

代码

#include <bits/stdc++.h>
using namespace std;

struct node
{
	int u;
	int v;
	int w;
}e[10009];

int n,m,d = 0,k;
int a[109][109],f[109];

void build()     //构图部分
{
	cin>>n>>m;
	for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= m; j++)
				{
					cin>>a[i][j];
				
					if (j > 1)          //对左右的方向构图
						d++,
						e[d].u = d,
						e[d].v = d+1,
						e[d].w = abs(a[i][j-1]-a[i][j]);
				}
			
			d++;
		}
		
	k = d+1;
	d = 0;
	for (int j = 1; j <= m; j++)               //对上下的构造
		{
			d = j;
			
			for (int i = 2; i <= n; i++)
				d += m,
				e[k].u = d - m,
				e[k].v = d,
				e[k].w = abs(a[i-1][j]-a[i][j]),
				k++;
		}
	
//	for (int i = 1; i <= k; i++)
//		cout<<e[i].u<<' '<<e[i].v<<' '<<e[i].w<<endl;
		
	k--;       //这里要减一下，因为多生成了一组无用的，不减去也没影响
}

int find(int x)       //寻根
{
	if (f[x] == x) return x;
	f[x] = find(f[x]);
	return f[x];
}

bool cmp(node a,node b)
{
	return a.w < b.w;
}

void kruskal()       //跑kruskal
{	
	long long sum = 0,cnt = 0;
	
	for (int i = 1; i <= n*m; i++) f[i] = i;
		
	sort(e+1,e+k+1,cmp);
	
	for (int i = 1; i <= k; i++)
		{
			int fu = find(e[i].u);
			int fv = find(e[i].v);
			
			if (fu != fv)
				{
				//	cout<<e[i].w<<endl;
					f[fv] = fu;
					sum += e[i].w;
					cnt++;
					
					if (cnt == k-1) break;
				}
		}
	
	cout<<sum;
}

int main()
{
	build(); 
	
	kruskal();
	
	return 0;
}