最长不下降子序列

最长不下降子序列

这个问题在DP中是很经典的，可以很好的用来理解DP的思想

设有一集合An={a1,a2,a3…an}，求其中的最长不下降子序列

我们可以将这个问题分解为多个子问题，分步求解

设有一数组：f[i]表示到第i个元素时的最长不下降子序列的长度

由此，我们便可以枚举，求出从第i个到第j个（j>i）的最长不下降子序列的长度，逐一比较，筛得最优

到这里我们便得到大体的程序框架了：

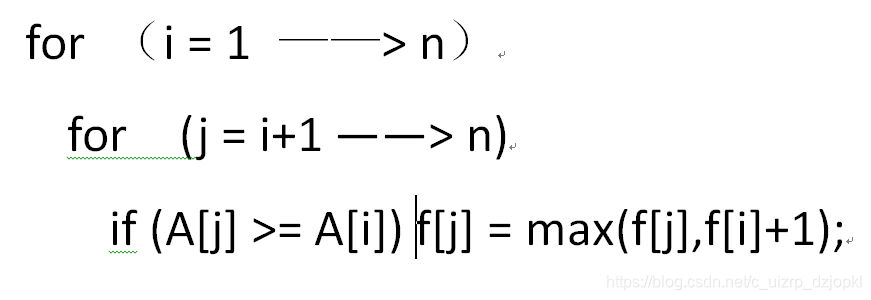
代码如下：

#include <bits/stdc++.h>
using namespace std;

int f[1009],a[1009];
int n,ans = 0;

int main()
{
	cin>>n;
	for (int i = 1; i <= n; i++) cin>>a[i];
	
	for (int i = 1; i <= n; i++)
		for (int j = i+1; j <= n; j++)
			if (a[j] > a[i]) 
				f[j] = max(f[i]+1,f[j])，
				ans = max(ans,f[i])
		
	cout<<ans+1;
	
	return 0;  
}

当然，我们的最长不下降子序列还有另一种写法——二分法
这种方法的时间复杂度是 O(nlogn)，很快

这种思路无非是边读边做的，每当读入一个数字，就判断当前的最优解中是否有其容身之处（容身之法也无非是直接在队尾添加），反之就将前方的一个二分到的与其最接近的那一个覆盖掉（是比那一个小的，这样可以更多的放置）

代码：

#include <bits/stdc++.h>
using namespace std;

int f[1009];
int n;

int binary_search(int k,int left,int right)
{
	while (left <= right)
	{
		int mid = (left + right) / 2;
		
		if (f[mid] == k) return mid;
		
		if (f[mid] < k) left = mid + 1;
		
		if (f[mid] > k) right = mid - 1;
	}
	
	return left;
}

int main()
{
	int tail = 0;
	
	cin>>n;
	for (int i = 1; i <= n; i++)
		{
			int x,p;
			cin>>x;
			
			if (x >= f[tail]) 
				tail++,
				f[tail] = x;
			
			if (x < f[tail])
				p = binary_search(x,1,tail),
				f[p] = x;
		}
		
	cout<<tail;
	
	return 0;
}