实验六 图像的傅里叶变换和频域处理

最近受了点刺激，早上睡不着，爬起来写文章，第一次写没经验请见谅。 

目录

实验目的

实验原理与方法

实验内容与步骤

---

实验六  图像的傅里叶变换和频域处理

• 实验目的

    1. 熟悉图像空间域和频率域的关系，掌握快速傅里叶变换

2. 掌握离散傅里叶变换的性质和应用

• 实验原理与方法

图像既能在空间域处理，也能在频率域处理。把图像信息从空域变换到频域，可以更好地分析、加工和处理

二维离散傅立叶正变换的表达式为

 

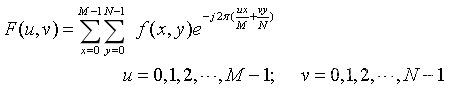
逆变换为：

 

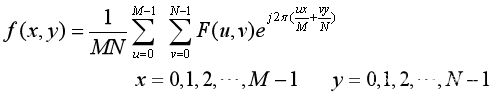
二维离散傅立叶变换具有若干性质，如：线性性、平移性、可分离性、周期性、共轭对称性、旋转不变性等。

可利用离散傅里叶变换，将信号从空间域变换到频率域，在频率域选择合适的滤波器H(u,v)对图像的频谱成分进行处理，然后经逆傅立叶变换得到处理图像，实现图像处理结果。

理想低通滤波的转移函数需满足以下条件:

H(u,v)  H(u,v)=1;     当D(u,v)<=Do时;

         H(u,v)=0;      当D(u,v)> Do时;

其中Do是一个非负整数, D(u,v)是反映点(u,v)到频率平面原点的距离。当小于Do的频率可以完全不受影响的通过滤波器,而大于Do的则完全不能通过滤波器,该Do可以形象的表示成截断频率。

理想高通滤波器的转移函数满足下列条件

H(u,v)   H(u,v)=0;     当D(u,v)<=Do时;

          H(u,v)=1;     当D(u,v)> Do时;

所得到的结果恰好与低通滤波相反, 当大于Do的频率可以完全不受影响的通过滤波器,而小于Do的则完全不能通过滤波器。

实验内容与步骤

• 

                                     （最好不要用这个图片，这个图片似乎有点问题） 

1．产生一幅如图所示亮块图像f(x,y)（256×256 大小、暗处=0，亮处=255）,对其进行FFT：

（1）同屏显示原图f 和FFT(f)的幅度谱图（提示：用二维傅里叶变换函数fft2，为避免傅里叶变换数据变化过大，显示其对数变换后结果log(1.001+abs(FFT(f))) ，用imshow或surf函数显示频谱）；

 

f=zeros(256,256);    
f(100:156,100:156)=255;    %自己创建一张图片
figure(1);
subplot(1,2,1),imshow(f,[]);title('原图');

F = fft2(f);
F = fftshift(F);
subplot(1,2,2),imshow(log(1+abs(F)),[]),title('FFT频谱');

运行结果：

 

 

（2）若令f1(x,y)=（-1）x+y f（x,y)，重复以上过程，比较二者幅度谱的异同，简述理由；

f1=zeros(256,256);    %按照要求改变灰度值
for x=1:256
    for y=1:256
        f1(x,y) = (-1)^(x+y)*f(x,y);
    end
end
F1 = fft2(f1);
F1 = fftshift(F1);    %计算f1的频谱图
figure(2);
subplot(2,2,1),imshow(f),title('原图');
subplot(2,2,2),imshow(log(1+abs(F)),[]),title('FFT频谱');
subplot(2,2,3),imshow(f1),title('f1原图');
subplot(2,2,4),imshow(log(1+abs(F1)),[]),title('f1TTF频谱图');

 

 

（3）若将f (x,y)顺时针旋转45 度得到f2(x,y)，试显示FFT(f2)的幅度谱，并与FFT(f)的幅度谱进行比较。（提示： 用imrotate函数对图像进行旋转）；

f2 = imrotate(f,45,'crop');    %旋转图片
figure(3),subplot(1,2,1),imshow(f2,[]),title('旋转后图像');
F2 = fftshift(fft2(f2));
subplot(1,2,2),imshow(log(1+abs(F2)),[]),title('f2FFT频谱图');

 

 

2. 对一幅256×256 大小、256 级灰度的数字图像进行频域的理想低通、高通滤波滤波，同屏显示原图、幅度谱图和低通、高通滤波的结果图。（提示：用二维傅里叶变换函数fft2，二维傅里叶逆变换函数ifft2，中心化函数fftshift，去中心化函数ifftshift。采用不同截断频率D0重复实验，观察结果）

低通滤波器：

%理想低通滤波器
figure(4);
subplot(221),imshow(f);
title('原图像');
f=im2double(f);
s=fftshift(fft2(f));%傅里叶变换，直流分量搬移到频谱中心
subplot(222), imshow(log(abs(s)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
h=zeros(a,b);%滤波器函数
res=zeros(a,b);%保存结果
a0=round(a/2);
b0=round(b/2);
d=40;
for i=1:a 
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<=d
            h(i,j)=1;
        else
            h(i,j)=0;
        end
    end
end
res=s.*h;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res),title('理想低通滤波所得图像'); 
subplot(224),imshow(h),title("理想低通滤波器图象");

 

 

高通滤波器： 

%理想高通
f=zeros(256,256);
f(100:156,100:156)=255;
figure(5);
subplot(221),imshow(f);
title('原图像');
f=im2double(f);
s=fftshift(fft2(f));%傅里叶变换，直流分量搬移到频谱中心
subplot(222), imshow(log(abs(s)+1),[]); 
title('图像傅里叶变换取对数所得频谱');
[a,b]=size(s);
h=zeros(a,b);%滤波器函数
res=zeros(a,b);%保存结果
a0=round(a/2);
b0=round(b/2);
d=40;
for i=1:a 
    for j=1:b 
        distance=sqrt((i-a0)^2+(j-b0)^2);
        if distance<d
            h(i,j)=0;
        else
            h(i,j)=1;
        end
    end
end
res=s.*h;
res=real(ifft2(ifftshift(res)));
subplot(223),imshow(res),title('理想高通滤波所得图像'); 
subplot(224),imshow(h),title('理想高通滤波器图像'); 

 

 

 不过这高、低通滤波器并不是我写的代码，具体参考此链接