Less is More: Recursive Reasoning with Tiny Networks

一、文章主要内容总结

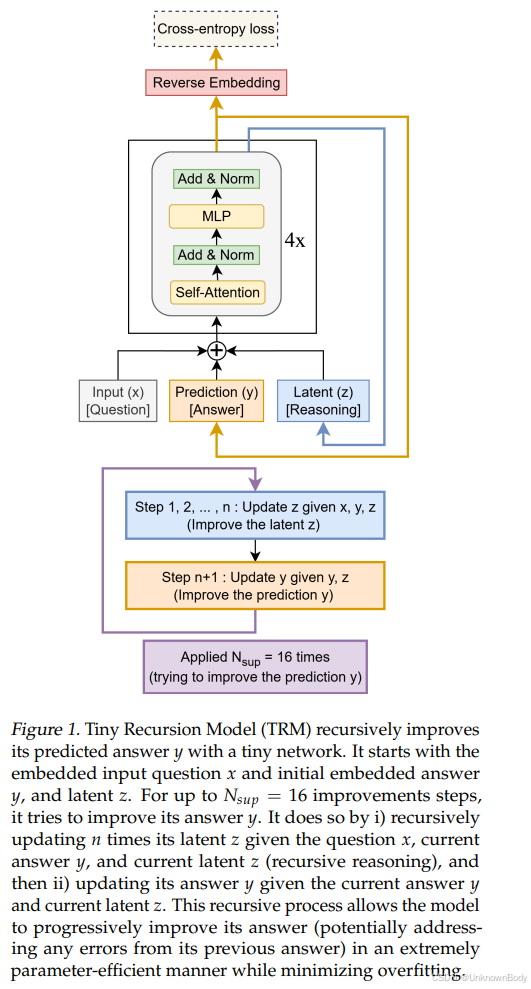
本文聚焦“小模型解决复杂推理任务”这一核心问题，针对现有方法（如大语言模型LLMs、分层推理模型HRM）的局限性，提出了** Tiny Recursive Model（TRM，微小递归模型）**，并通过实验验证其优越性。

1. 研究背景与现有方法痛点

• LLMs的不足：生成答案时采用自回归方式，单个错误token会导致整体答案无效；依赖思维链（CoT）和测试时计算（TTC）提升可靠性，但CoT成本高、需高质量推理数据且易生成错误推理，TTC无法完全解决复杂任务（如ARC-AGI系列任务）的性能瓶颈，且参数量极大（通常数十亿至上万亿）。
• HRM的局限性：HRM通过两个小网络（高频的(f_L)和低频的(f_H)）递归推理+深度监督，在数独、迷宫等任务上表现优于LLMs，但存在理论依赖强（需假设递归达到不动点以应用隐函数定理IFT和1步梯度近似，实际难满足）、结构复杂（两个网络+生物层级解释）、训练效率低（自适应计算时间ACT需额外前向传播）、参数量仍较高（27M）等问题。

2. TRM的核心设计

TRM以“简化结构、提升泛化、减少参数”为目标，核心设计包括：

• 单网络架构：用