PSpice测量定义与应用

性能分析

12.1. 测量函数

PSpice 包含了50多种测量定义，其中一些列在 表 12.1中。完整的列表见附录。第10章练习2中使用了标准的中心频率和带宽定义。然而，测量定义还允许您指定希望进行测量的范围。例如，CenterFrequency_XRange 定义允许您在指定的 x‐范围（即频率范围）内对波形进行测量。您还可以自定义设计自己的测量定义。

12.2. 测量定义

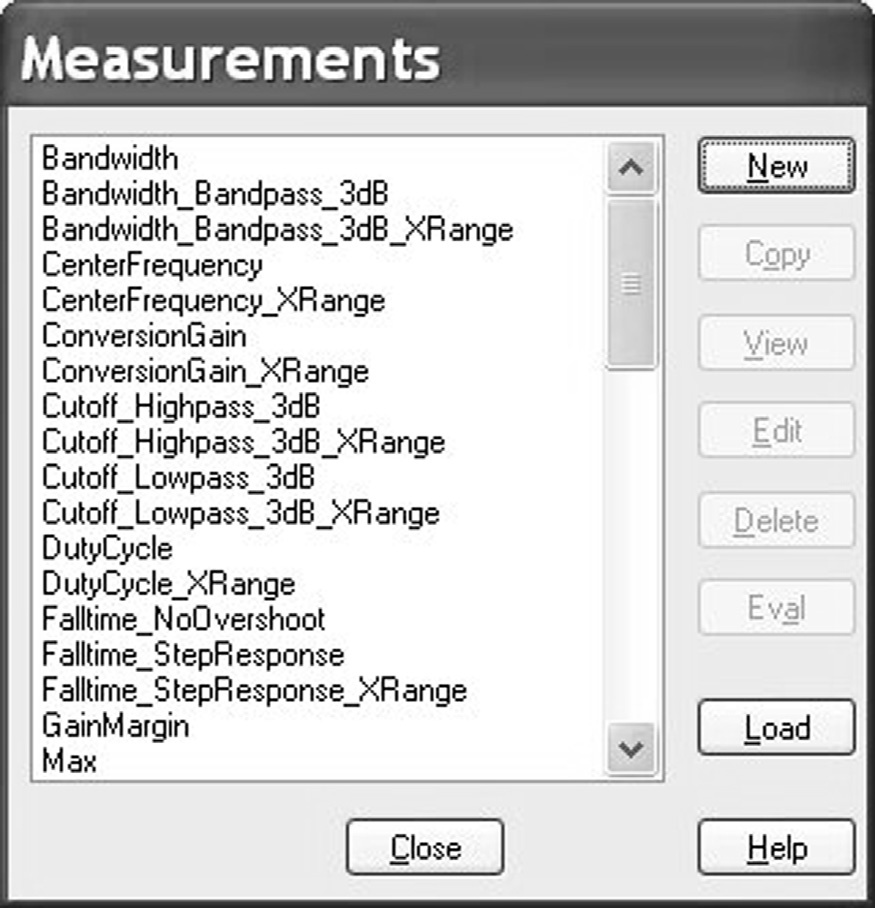
测量定义可以在PSpice中通过轨迹>测量查看，该选项显示所有可用测量以及创建、查看、编辑和评估测量的各种选项（图12.1）。

表 12.1 PSpice 中可用的一些测量定义

定义	描述
带宽	波形的带宽（您选择分贝级别）
带宽_带通_3分贝	波形的带宽（3 分贝水平）
中心频率	波形的中心频率（分贝水平）
中心频率_XRange	波形在指定范围内的中心频率（分贝值）
x范围	转换增益 第一个波形的最大值的比率 第二个波形的最大值
截止_高通_3分贝	高通带宽（对于给定dB水平）
截止_低通_3分贝	低通带宽（对于给定dB水平）
占空比	第一个脉冲/周期的占空比
下降时间_无过冲	无过冲时的下降时间
Max	波形的最大值
Min	波形的最小值
第n个峰值	波形在第n个峰值处的值
超调	阶跃响应曲线的超调
峰值	波形在第n个峰值处的峰值
相位裕度	相位裕度
脉冲宽度	第一个脉冲的宽度
Q_带通	计算带通的Q值（中心频率/带宽） 在指定分贝点的响应
无过冲上升时间_	无超调的阶跃响应曲线的上升时间
上升时间_阶跃响应	阶跃响应曲线的上升时间
稳定时间	从 到阶跃响应所需的时间 在指定范围内稳定下来
下降转换速率_	负向阶跃响应曲线的转换速率

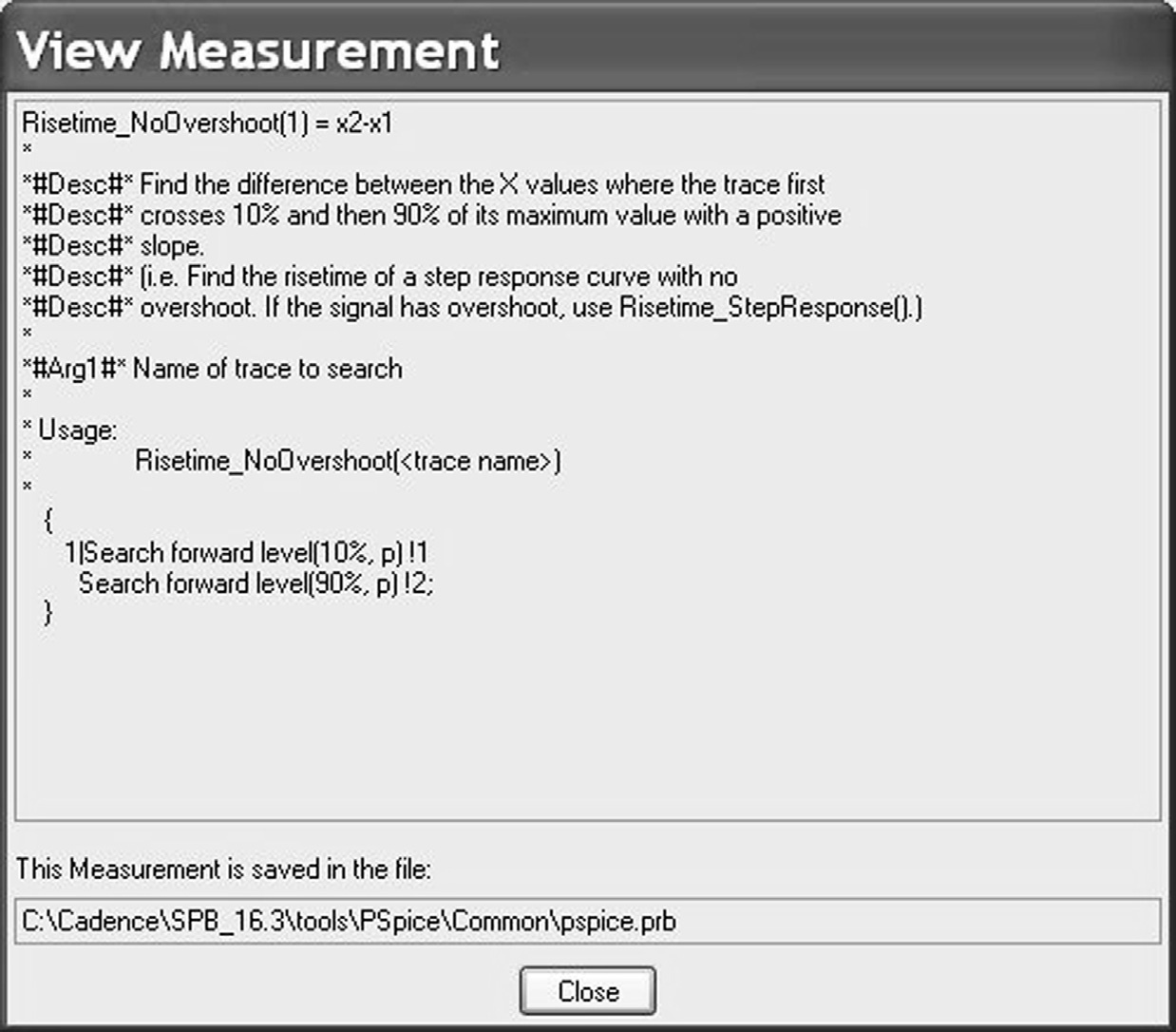
例如，图 12.2 显示了无过冲上升时间的测量定义_NoOvershoot。

上升时间，根据定义，是指电压或电流达到最大值的10%和90%时对应的时间差。因此需要进行两次测量：一次在电压（或电流）曲线达到最大值的 10%时（x1），另一次在曲线达到最大值的90%时（x2）。

为了找到曲线上10%和90%处的点，使用了搜索命令： Search forward level(10%,p) !1 Search forward level(90%,p) !2

在此示例中，在正向（p）搜索10%电平并返回第一个数据点（x1），同时在正向（p）搜索90%电平并返回第二个数据点（x2）。

中的第一行 图 12.2 称为标记点表达式（有一个值），用于计算 x2 与 x1 之间的差值（x2 - x1）。以 #开头的任何行都是注释行，为用户提供信息。

12.3. 练习

练习1

1. 创建一个名为Risetime的项目，并绘制图12.3中的CR电路。确保将节点命名为out，如图所示。
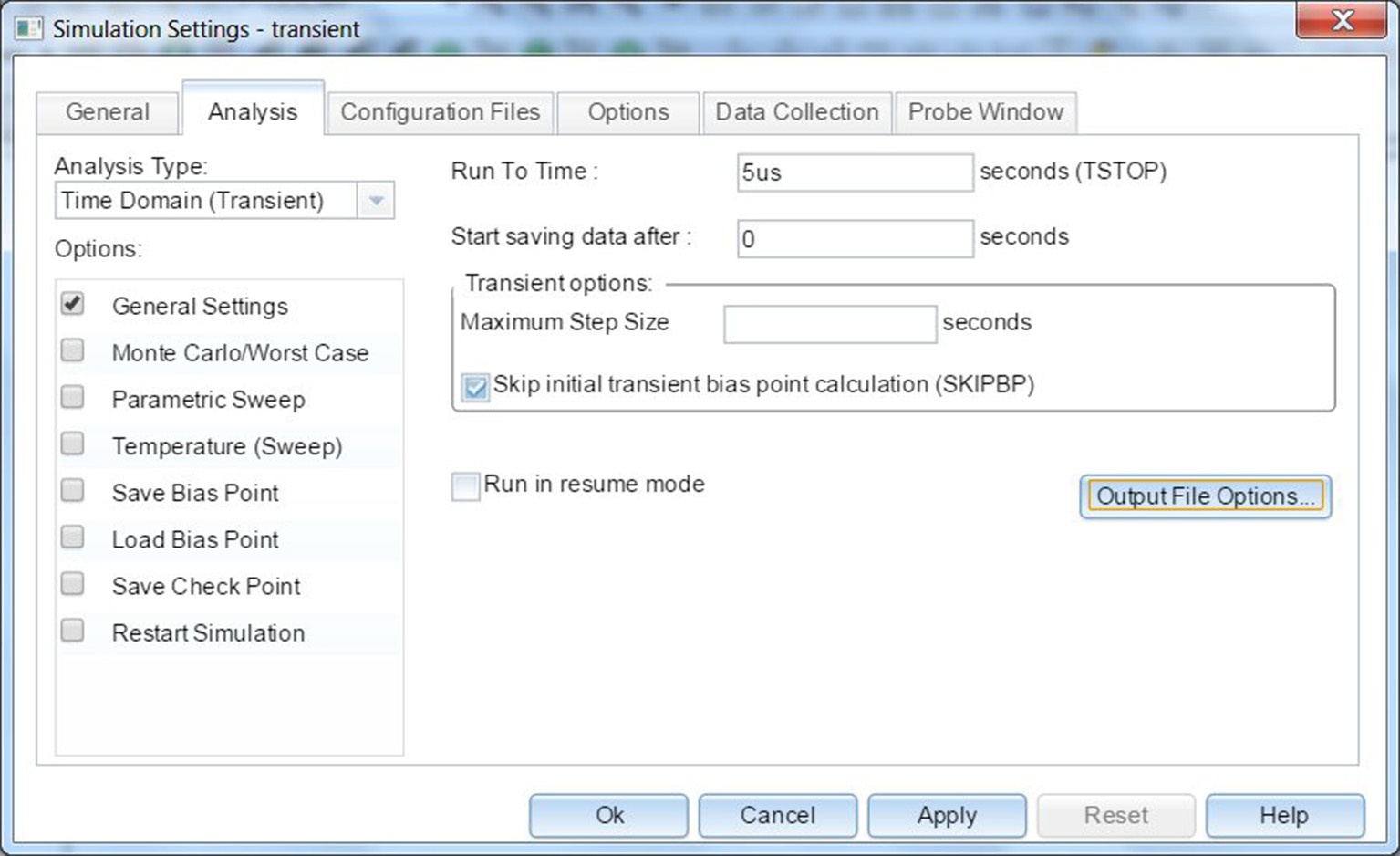
2. 创建一个PSpice瞬态分析，运行至时间设置为 5 μ秒。
3. 在节点out上放置一个电压标记。
4. 运行仿真。
5. 您将看到一条电压的水平直线（图 12.4）。这是因为在瞬态分析之前已执行了直流偏置点分析，导致电容已达到10伏特的稳态电压。因此，在时间t = 0秒时，电容两端的电压为10伏特，如图所示。

0s
4V
8V
12V
16V
0.5 微秒 1.0 微秒 1.5 微秒 2.0 微秒 2.5 微秒
Time
3.0 微秒 3.5 微秒 4.0 微秒 4.5 微秒 5.0 微秒
V(输出)

6. 可以放置一个初始条件，从专用库中选择IC1元件，以确保在时间t = 0s时，电容两端的电压为0伏特，如第7章练习2所示。或者，在本例中，勾选仿真配置中的跳过初始瞬态偏置点计算（图12.5），然后运行仿真。
7. 您应该会看到电容两端熟悉的指数电压上升（参见图 12.6）。

0s
0V
5V
10V
0.5 微秒 1.0 微秒 1.5 微秒 2.0 微秒 2.5 微秒
Time
3.0 微秒 3.5 微秒 4.0 微秒 4.5 微秒 5.0 微秒
V(输出)

练习2

您将测量萨伦‐凯滤波器的低通截止频率。

1. 绘制 图12.9 中的萨伦‐凯滤波器。
2. 设置交流扫描为1赫兹到10千赫兹，进行每十倍频程20个点的对数扫描。
3. 在输出端放置一个VdB电压标记： PSpice> 标记 >高级 >电压的分贝幅值。
4. 运行仿真。
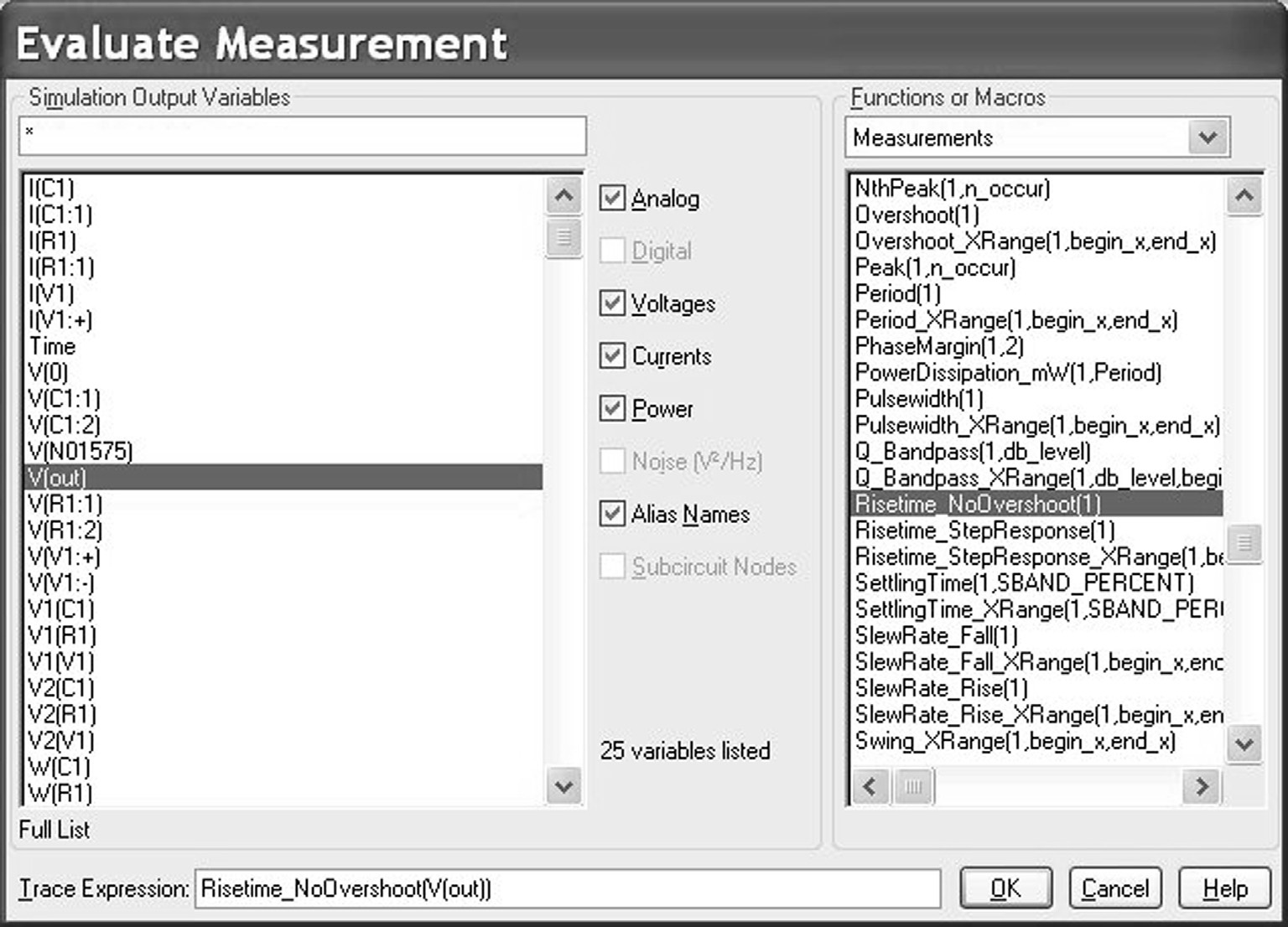
5. 在 PSpice 中选择 轨迹 > 评估测量 >截止_低通_3dB()并选择 V(输出)。轨迹测量应显示截止频率为 99.6赫兹，如 图12.10 所示。

6. 频率响应如图12.11所示。

1.0 赫兹 3.0 赫兹 10 赫兹 30 赫兹 100 赫兹 300 赫兹 1.0 千赫兹 3.0 千赫兹 10 千赫兹
–80
0
–40
40
频率 DB(V(输出))