异常值分析方法

异常值分析原理

异常值指的是样本中的一些数值明显偏离其余数值的样本点，所以也称为离群点。异常值分析就是要将这些离群点找出来，然后进行分析。常见的分析方法有三种：简单统计量分析、3σ 原则、箱型图分析。
简单的介绍一下简单统计量分析和3σ 原则，本文主要还是介绍箱型图分析，这是一个比较通用的方法。简单统计量分析主要就是看看最大值和最小值等等，判断其是否超过了范围，有明显的错误。3σ 原则则是在数据服从正态分布的时候用的比较多，在这种情况下，异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值。
而箱型图是根据实际的数据绘制的，没有什么限制性要求，比较通用。识别标准如下：异常值被定义为小于(QL - 1.5IQR)或大于QU + 1.5IQR的值。其中QL为下四分位数，即有25%的数值比它小，QU为上四分位数，IQR=QU-QL。这个必须要利用作图函数来进行绘制图形，才好观察数据集中存在的一些异常值。

箱型图作图方法

DataFrame.boxplot(column=None, by=None, ax=None, fontsize=None, rot=0, grid=True, figsize=None, layout=None, return_type=None, **kwds)
column：选择多少列来作图，主要是以list of str的形式。
by：主要是来指定分组情况，可以借用第三个变量，第三个变量也是list of str形式。
layout:这个参数主要就是进行显示时的布局，以元祖的形式例如：(2,1)。
rot：斜度，让坐标倾斜。
grid：当想对箱线图进行其他格式化的时候，可以令grid=False。
return_type：返回的类型，当你想在图画出来后调整外观，如fliers,caps,boxes,medians,whiskers将会在dict中，则令return_type=‘dict’。
下面以python代码简单的运用一下这些参数：

import numpy as np
import pandas as pd
df = pd.DataFrame(np.random.randn(10,3),columns=['col1','col2','col3'])
#增加第三个变量X
df['X'] = pd.Series(['A','A','A','A','A','B','B','B','B','B'])
#做箱线图
p = df.boxplot(column=['col1','col2'],by='X',layout=(2,1),grid=False,rot=45,fontsize=15)

运行结果如下：

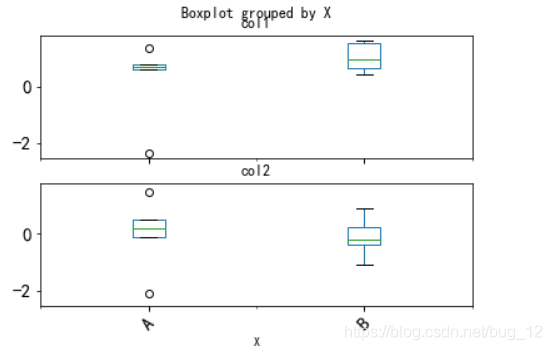
这只是我们造的少量数据，在现实的数据集中是存在异常值的。下面以一个餐饮销量的数据集来进行异常值分析，分析之前首先介绍一个方法来对图中的点进行注释。
plt.annotate(s, xy, *args, **kwargs)
s：注释的内容。
xy：注释点(箭头指向)的位置。
xytext：注释内容的位置。
arrowprops: 通过arrowstyle表明箭头的风格或种类

异常值分析(箱线图)实战

首先先看一下这个数据集的样子是什么样子的，如下图：

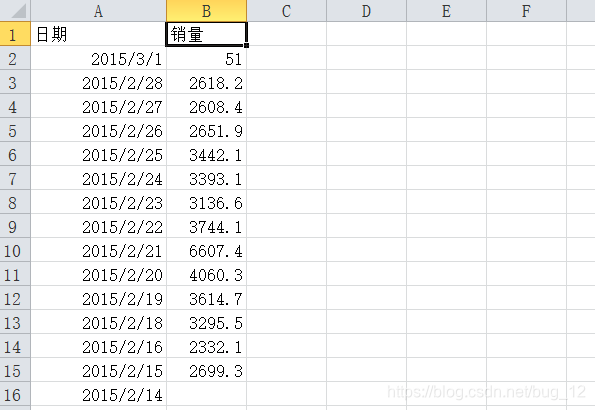
属性为两列，一个是日期，一个是销量，下面以日期为索引。

import pandas as pd
import matplotlib.pyplot as plt
#餐饮数据
catering_sale = 'G:\data\Python\chapter3\demo\data\\catering_sale.xls'
data = pd.read_excel(catering_sale,index_col = u'日期')
# print(data.head())
plt.rcParams['font.sans-serif'] = ['SimHei']
#正常显示负号
plt.rcParams['axes.unicode_minus'] = False
plt.figure()
#箱线图
p = data.boxplot(return_type='dict')
#异常值坐标
x = p['fliers'][0].get_xdata()
y = p['fliers'][0].get_ydata()
y.sort()
print(x)
print(len(x))
print(y)
#用annotate添加注释
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i],xy=(x[i],y[i]), xytext=(x[i]+0.05 - 0.8/(y[i]-y[i-1]),y[i]))
    else:
        plt.annotate(y[i],xy=(x[i],y[i]), xytext=(x[i]+0.08,y[i]))
#展示图        
plt.show()

运行结果如下：

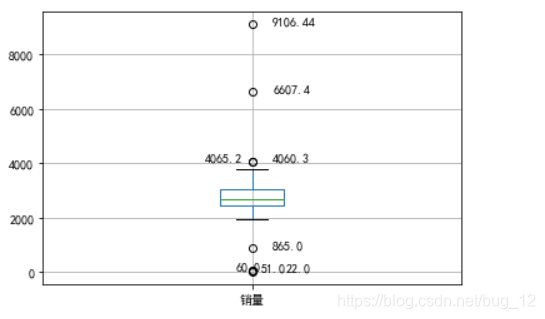
从图中可以清楚的看到，有些值偏离了很多，例如22、51、60、6607.4、9106.44等，这些归为异常值，从而可以确定过滤规则为销量在400一下5000以上的为异常数据。