Dynamic Anticipation and Completion for Multi-Hop Reasoning over Sparse Knowledge Graph

在稀疏知识图谱上进行动态预测/完备的多跳推理

多跳推理已被广泛研究,近年来寻求一种有效且可解释的知识图谱（KG）补全方法。以前的大多数推理方法是为实体之间具有足够路径的密集 KG 设计的，但在那些仅包含用于推理的稀疏路径的稀疏 KG 上效果不佳。一方面，稀疏的 KGs 包含的信息较少，这使得模型难以选择正确的路径。另一方面，缺乏指向目标实体的证据路径也使推理过程变得困难。为了解决这些问题，我们通过应用新颖的动态预测和完成策略，提出了一种名为 DacKGR 的稀疏 KG 多跳推理模型：

（1）预测策略利用基于嵌入的模型的潜在预测使我们的模型执行更多稀疏 KG 上的潜在路径搜索。
(2) 基于预期信息，完成策略在路径搜索过程中动态添加边作为附加动作，这进一步缓解了 KG 的稀疏问题。从 Freebase、NELL 采样的五个数据集的实验结果和维基数据表明我们的方法优于最先进的基线

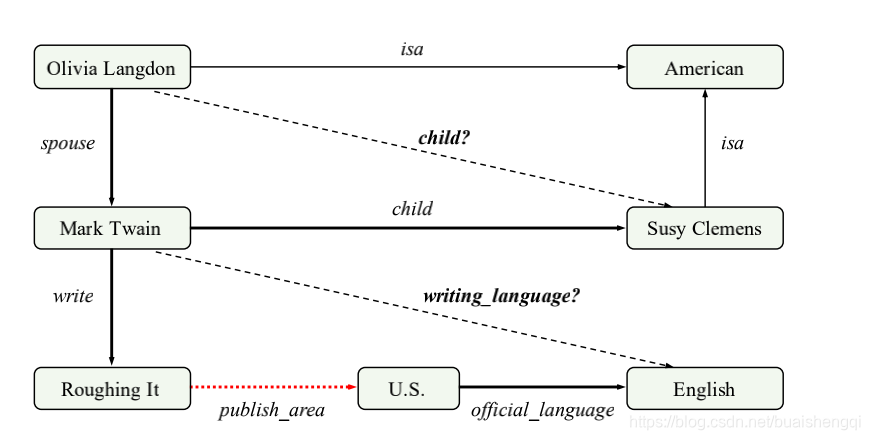
图 1：稀疏 KG 上的多跳推理任务的说明。 实体之间缺失的关系（黑色虚线箭头）可以通过推理路径（粗箭头）从现有的三元组（黑色实心箭头）推断出来。 然而，稀疏 KG 中缺少推理路径中的一些关系（红色虚线箭头），这使得多跳推理变得困难。 

稀疏KGs的问题：（1）信息不足。 与普通 KG 相比，稀疏 KG 包含的信息较少，这使得代理很难选择正确的搜索方向。
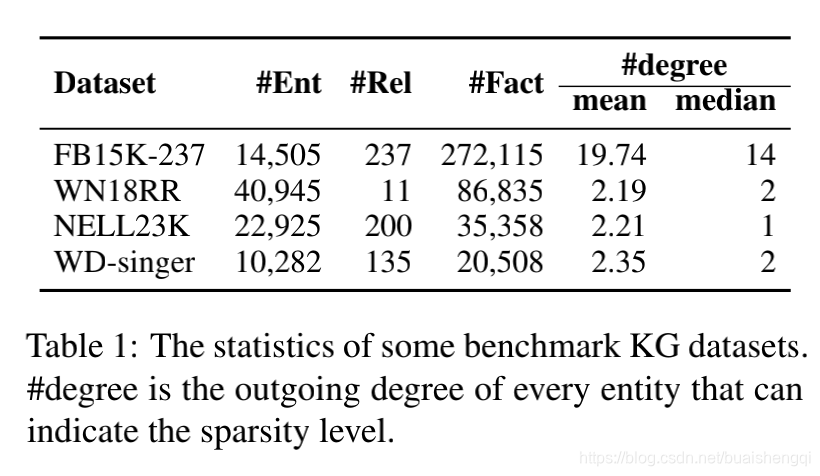
(2) 缺少路径。 在稀疏的 KG 中，一些实体对之间没有足够的路径作为推理证据，这使得代理很难进行推理过程。 如图所示在图 1 的下半部分，由于缺少关系发布区域，因此马克吐温和英语之间没有证据路径。 从表 1 我们可以了解到，一些采样的 KG 数据集实际上是稀疏的。 此外，一些特定领域的 KG（例如 WD-singer）没有丰富的知识，也面临着稀疏的问题。

我们提出了一种多跳推理名为 DacKGR 的模型，以及两个动态解决上述两个问题的策略 

动态预测:利用稀疏 KG 中的有限信息在推理过程之前预测潜在目标。 与多跳推理模型相比，基于嵌入的模型对稀疏 KG 具有鲁棒性，因为它们依赖于每一个三元组而不是 KG 中的路径。 为此，我们的预期策略将预训练的基于嵌入的模型的预测作为预期信息注入到强化学习。 该信息可以指导代理避免漫无目的地搜索路径。

动态补全
在推理过程中临时扩展KG的部分以丰富路径扩展的选项。 在稀疏 KG 中，许多实体只有很少的关系，这限制了代理的选择空间。 因此，我们的补全策略根据当前实体在搜索推理路径期间的状态信息动态添加了一些额外的关系（例如，图 1 中的红色虚线箭头）。 之后，对于当前实体和附加关系 r，我们 使用预训练的基于嵌入的模型来预测尾部实体 e。 然后，附加关系 r 和预测的尾部实体 e 将形成一个潜在的动作 (r, e) 并添加到 用于路径扩展的当前实体。 我们对从 Freebase、NELL 和 Wikidata 采样的五个数据集进行了实验。 结果表明，我们的模型 DacKGR 优于以前的多跳推理模型，这验证了验证了我们模型的有效性。

给定一个图 KG 和一个三重查询 (es, rq, ?)，其中 es 是源实体，rq 是查询关系，知识图的多跳推理旨在预测 (es, rq ，？）。与之前的 KG 嵌入任务不同，多跳推理还给出了一个支持路径 {(es, r1, e1),(e1, r2, e2)。 . . ,(en-1, rn, eo)} 超过 KG 作为证据。如上所述，我们主要本文重点关注稀疏 KG 上的多跳推理任务。

3 方法论
在本节中，我们首先介绍多跳推理的整个强化学习框架，然后详细介绍我们为稀疏 KG 设计的两种策略，即动态预测和动态补全。 前一种策略从基于嵌入的模型中引入指导信息，以帮助多跳模型在稀疏 KG 上找到正确的方向。 基于这种策略，动态补全策略在推理过程中引入了一些额外的动作来增加路径数，可以缓解 KG 的稀疏性。DacKGR 的整体框架如图 2 所示。

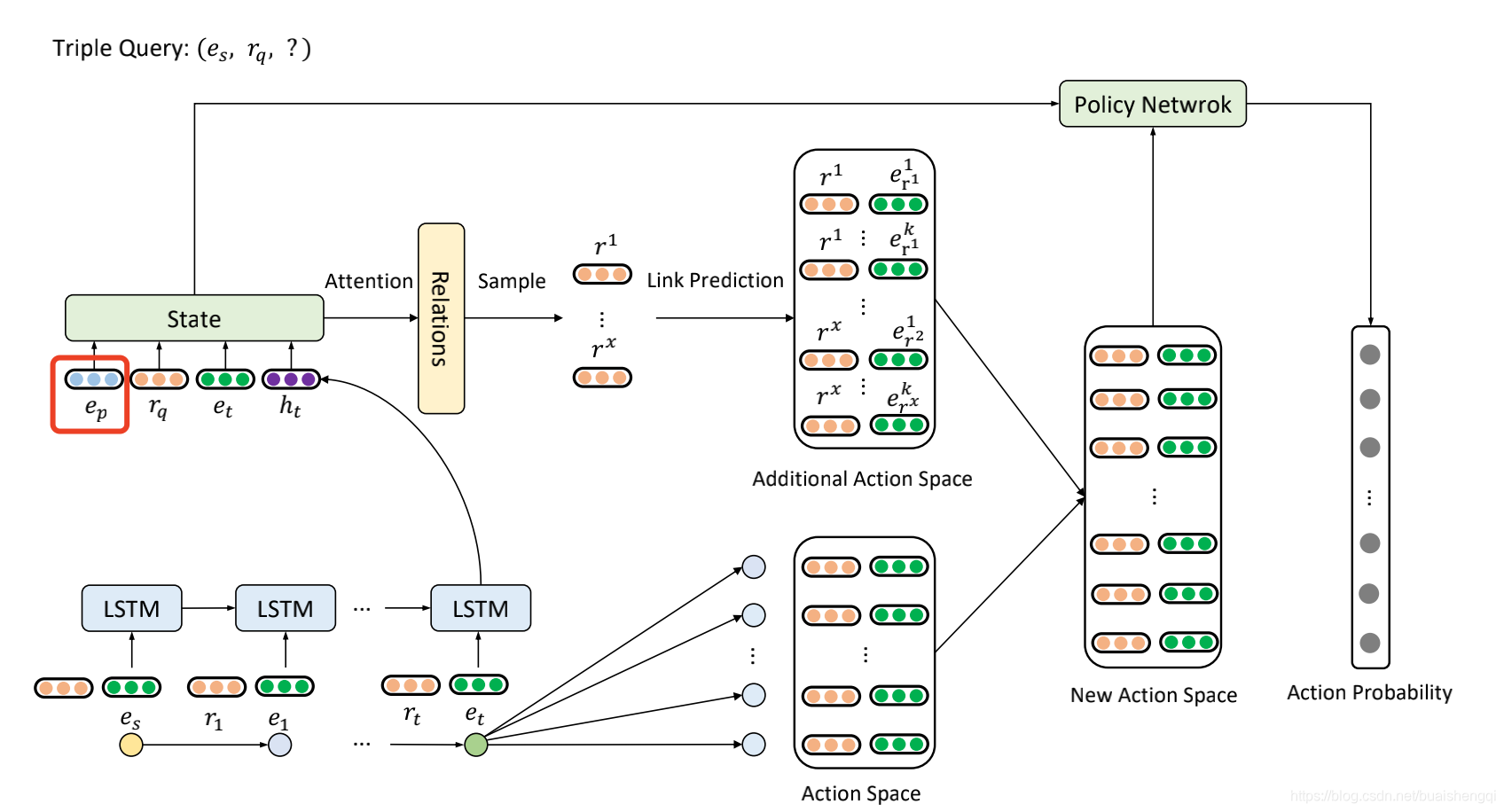
 图 2：具有动态预期和动态补全策略的策略网络说明。 ep的向量就是3.3节介绍的预测信息。 我们使用当前状态动态选择一些关系，并使用预训练的基于嵌入的模型进行链接预测以获得额外的动作空间。 原来的动作空间将与附加的动作空间合并，形成一个新的动作空间。 

强化学习框架:

状态
  在多跳推理过程中，agent选择哪条边（关系）不仅取决于查询关系rq和当前实体 et，而且在以前的历史搜索路径上。 因此，第 t 跳的状态可以定义为 st = (rq, et, ht)，其中 ht 是历史路径的表示。 具体来说，我们使用 LSTM 对历史路径信息进行编码，ht 是 LSTM 在第 t 步的输出。

动作 对于状态 st = (rq, et, ht)，如果有KG 中的三元组 (et, rn, en)，(rn, en) 是状态st一个动作。状态 st 的所有动作构成其动作空间 At = {(r, e)|(et, r, e) ∈ T }。此外，对于每个状态 st，我们还添加了一个额外的 action(rLOOP, et)，其中 LOOP 是手动添加的自循环关系。它允许代理停留在当前实体，这类似于“停止”动作。 Transition 如果当前状态是 st = (rq, et, ht) 并且代理选择 (rn, en) ∈ At 作为下一个动作，则当前状态 st 将转换为 st+1 = (rq, en, ht+1)。在本文中，我们将最大跳数限制为 T，并且转换将在状态 sT = (rq, eT , hT ) 处结束。
奖励对于具有黄金尾实体 eo 的给定查询 (es, rq, ?)，如果代理最终停在正确的实体处，即 eT = eo，则奖励为 1，否则，奖励是由函数 f(es, rq, eT ) 给出的 0 到 1 之间的值，其中函数 f 由预训练的知识给出用于评估三元组 (es, rq, eT ) 正确性的图嵌入 (KGE) 模型。 

策略网络

动作(r,e)在t跳可以表示为:at = [r; e],r,e分别是向量,代理选择的每个动作的表示 将被送入 LSTM 以生成迄今为止的历史路径信息.

h t = LSTM ( h t- 1 , a t- 1 ) .

第t个状态

s t = ( r q , e t , h t ) 被表示为  s t = [ r q ; e t ; h t ] .

我们通过将 At 中的所有动作堆叠为 At

策略网络表示为:

 

π θ ( a t | s t ) = σ ( A t ( W 1 ReLU ( W 2 s t )))

其中 σ 是 softmax 算子，W1 和 W2 是两个线性神经网络，πθ(at|st) 是At 中所有动作的概率分布。

3.3 动态预期
正如之前的工作（Das 等人，2018 年；Lin 等人，2018 年）所报告的那样，虽然 KGE 模型不可解释，但它们可以在大多数 KG 上获得比多跳推理模型更好的结果。
这种现象在稀疏 KG 上更为明显（参见表 3 中的实验结果），因为 KGE 模型更加稳健，因为它们不依赖于 KG 的连通性。 受上述现象的启发，我们提出了一种新的策略，称为动态预测，它引入了预测信息基于嵌入的模型到多跳推理模型中以指导模型学习。 具体来说，对于三重查询 (es, rq, ?)，我们使用预训练的 KGE 模型来获得所有实体都是尾实体。 形式上，概率向量可以表示为 p ∈ R|E|，其中 p 的第 i 个维度的值表示 ei 是正确尾实体的概率。

对于动态预期策略，我们改变等式 2 中的状态表示为

s t = [ e p ; r q ; e t ; h t ]

其中 ep 是 KGE 模型给出的预测信息。 在本文中，我们使用以下三种策略来生成 ep：（1）样本策略。 我们根据概率分布对实体进行采样p 并将其向量表示为 ep。 (2) 第一战略。 我们选择 p 中概率最高的实体。 (3)平均策略。 我们根据以下公式对所有实体的向量取加权平均概率分布 p 作为预测信息 ep。 在实验中，我们选择在有效集合上表现最好的策略。

3.4 动态补全

在稀疏的 KG 中，头部和尾部实体之间的证据路径往往不足，从而导致多跳推理模型的性能显着下降。 为了解决上述问题，我们提出了一种称为动态完成的策略，在推理过程中动态地增加每个实体的动作空间。 具体来说，对于当前状态 st,其附加动作的候选集可以定义为

 

C t = { ( r, e ) | r ∈ R ∧ e ∈ E ∧ ( e t , r, e ) T } .

我们需要从 Ct 中选择一些概率最高的动作作为附加动作，其中概率可以定义为

 

p (( r, e ) | s t ) = p ( r | s t ) p ( e | r, s t )

由于Ct 的规模很大,因此可先进行关系r的选择，再根据r选择实体e。对于当前状态st，我们计算attention所有关系的值作为 p(r|st)，

w = Softmax ( MLP ( s t ) · [ r 1 , · · · , r |R| ])

我们定义一个参数α来控制比例需要添加的操作。 此外，我们还有一个参数 M 表示附加动作的最大数量。 因此，该附加动作的数量可以定义为

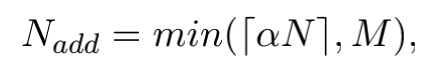
其中 N 是当前状态的动作空间大小。 有了注意力向量 w 后，我们选择 w 中注意力值最大的前 x 个关系，形成一个新的关系集

 

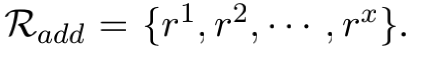
 参考文章:

https://zhuanlan.zhihu.com/p/266481902