基于QCA的多路复用器模块化设计

基于多路复用器的可靠量子点细胞自动机逻辑电路模块化设计

摘要

随着超大规模集成电路（VLSI）技术的快速发展，实现具有低功耗的可靠设计已成为当务之急。量子点细胞自动机（QCA）作为一种纳米级架构，因此成为当前CMOS超大规模集成电路的一种可行替代方案。本工作旨在设计QCA中的逻辑模块。提出了一种模块化设计方法，用于构建具有优化线路交叉、延迟和功耗的容错 2n:1多路复用器。本文提出一种2:1 QCA多路复用器作为基本逻辑模块，并进一步用于合成4:1和8:1多路复用器。相较于现有设计，在时钟速度（36%）、线路交叉（58%）、容错能力（77.62%）和功耗方面均取得了显著成果。通过合现场可编程门阵列（FPGA）的可配置逻辑块（CLB），进一步验证了本文提出的多路复用器的有效性。

1. 引言

当前CMOS器件的尺寸缩小到一定程度以下并不可行，因为在纳米级尺度下会引发异常的量子行为。量子点细胞自动机（QCA）作为一种新兴的纳米技术，被认为是CMOS技术的一种潜在替代方案，并为CMOS的基本局限性提供了解决方案。QCA的主要优势在于其高器件密度以及在纳米级时代的计算速度[1]。目前实现的大多数QCA设计仅采用共面线路交叉。但共面线路交叉极易受到随机外部效应和串扰的影响[2]。

多路复用器在识别布尔函数以及电路设计中起着关键作用，例如在现场可编程门阵列（FPGA）、控制逻辑块（CLB）和存储器电路的设计中。文献[3]研究了一种进化方法，旨在利用与和或逻辑块等基本构建单元实现模块化的 2n选1多路复用器。但该设计中使用了延迟块和额外的接口电路，导致电路延迟和复杂性显著增加。此外，在合成高阶多路复用器时，无法有效级联两个独立的低阶多路复用器模块。而且，现有文献尚未妥善解决模块化多路复用器在容错能力方面的可靠性问题以及功耗优化问题。

上述因素要求在具有较少线路交叉的模块化设计与其相关的容错能力及功耗之间的可靠性之间进行权衡。在此背景下，本研究提出了一种用于量子细胞自动机的模块化设计方法

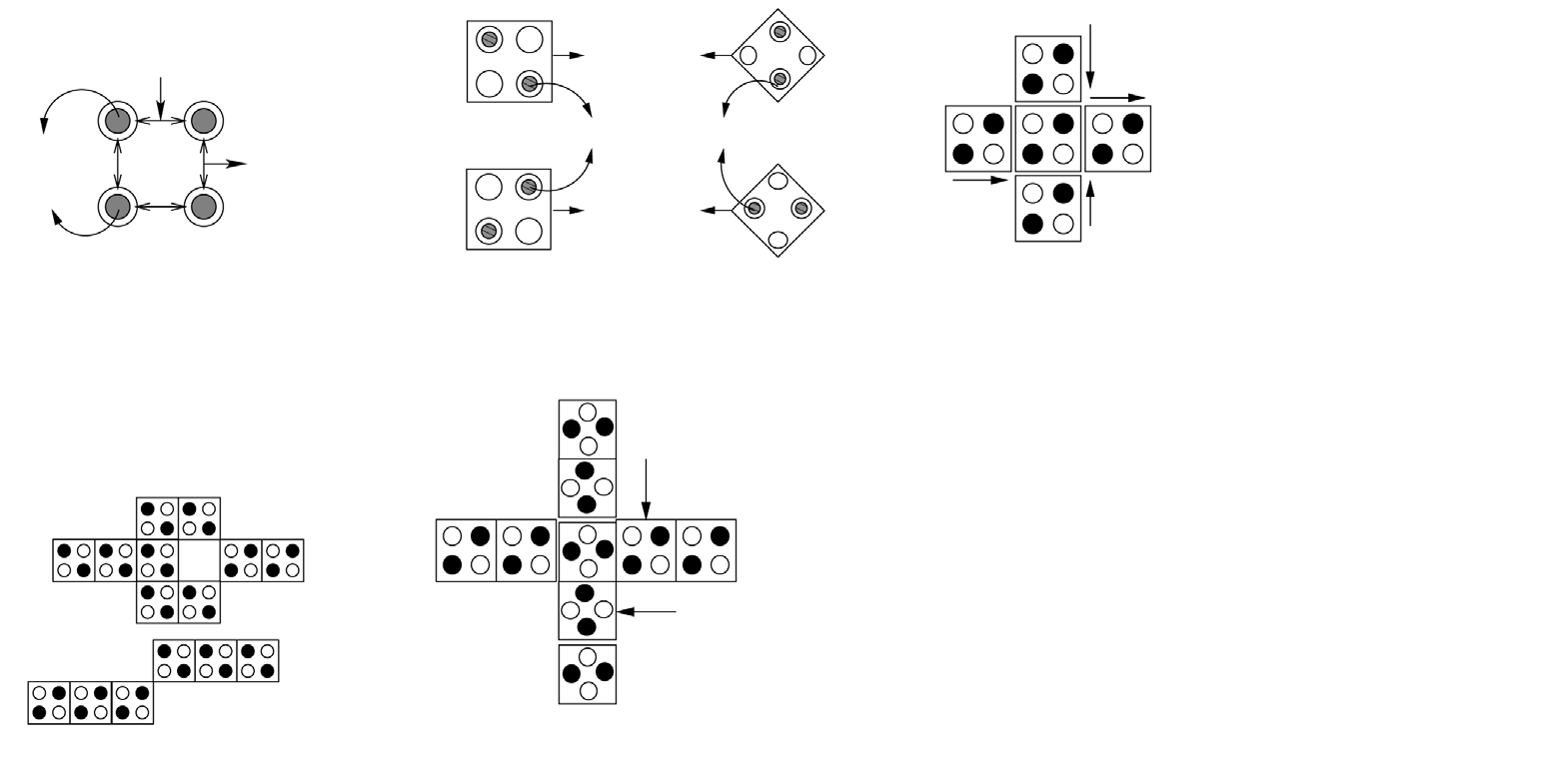
量子细胞。(b) 具有两种不同极化的量子点细胞。(c) 多数逻辑门。(d) 反相器。(e) 线路交叉。(f) 时钟。)

2. 预备知识

一个方形的量子细胞自动机单元在其四个角上包含四个量子点（图1(a)）。其中电子在量子力学上被限制[1]，在标准无故障的量子细胞自动机单元中，共有两个电子。由于库仑排斥，电子占据单元的对角位置，从而形成两种稳定的构型，其极化分别为 P = −1（逻辑‘0’）和 P = +1（逻辑‘1’），如图1(b)[1]所示。当一个量子细胞自动机单元从逻辑状态1翻转到0时，并没有像传统CMOS那样实际的电容放电过程，因为状态1和0是由量子细胞自动机单元中电子的位置决定的。此外，极化沿单元的传播是由于相邻量子细胞自动机单元中电子之间的相互作用所致。采用四个独立且级联的时钟相位来同步量子细胞自动机单元[1]，如图1(f) 所示，以实现信息（极化）的传播。时钟不仅控制信息传播，还为量子细胞自动机电路提供所需能量。

最基本的QCA结构是多数投票器，其功能可由MV(A, B, C)描述= Maj(A, B,C)=AB+ BC+ CA（图1(c)）。如有需要，可通过将多数投票器的一个输入固定为常量来导出与/或门（−1)/(+1。QCA中的反相器可通过两种不同方式实现，如图1(d)所示。此外，线路交叉可实现为共面或多层形式。共面线路交叉需要45°（+‐单元）旋转的单元和90°（×‐单元）单元，如图1(e)所示。由于制造上的限制，目前实现多层线路交叉的研究非常少。

3. 相关工作

已经有一些尝试围绕量子点细胞自动机多路复用器设计高效的逻辑电路。本文首次提出了一种模块化设计方法，用于构建 2n:1多路复用器。在这种设计中，使用了与门、或门和延迟（模块化）

二进制‘0’
P = −1
二进制‘1’
P = +1 90 − degree orientation
局域电子
(b)
F Maj
C B A
F = AB + BC + CA
A
C
B F
(c)
输入
T/4 T/2 3T/4 T
输出
Hold发布 开关 放松
A
输出 输入
A’
A’ A
量子
well
结 隧道
隧道掘进 潜力
(a)
’+’ 细胞
’X’ 细胞
B
B
A A
(d) (f) (e)

使用了延迟块。然而，由于大量的延迟块和额外的接口逻辑，导致电路延迟和复杂性变得不可接受。随着多路复用器的阶数增加，延迟块的数量以及额外的接口（包括代价较高的线路交叉）也随之增加。

在[4]中，提出了一种设计量子细胞自动机（QCA）多路复用器的新方法，以克服QCA中不可避免的共面线路交叉问题。该方法采用单一分布网络。将信号分布网络与组合逻辑门分离，虽然提升了系统性能，但代价是增加了时钟周期以及具有大量线路交叉的复杂设计布局。然而，所有这些尝试均未能解决可靠性问题，无法实现高容错且能量高效的逻辑电路。

4. 多路复用器的提出的架构

据报道，首次尝试设计一种高效多路复用器见于[5]。该设计假设有三个时钟区域。为了使其更高效且延迟更小，我们提出了一种仅包含两个时钟区域的设计（图3(a)）。所提出的2:1量子细胞自动机多路复用器的逻辑功能为
OUT = I1·S + I0·S̄
其中，I0 和 I1 是两个数据输入和S是选择线。即，
OUT = Maj(Maj(S, I0, 0), Maj(S, I1, 0), 1) = Maj(S·I0, S·I1, 1) = S·I0 + S·I1
从上述推导可以得出，一个2:1 多路复用器需要3个多数门和1个反相器，如图2所示。图3(a)示意图中的所有逻辑元件均用颜色标示以表示不同的时钟区域。所有输入（I0、I1和S）位于同一个时钟区域，而输出位于另一个时钟区域。这使得时钟相位能够按正确的顺序（0, 1, 2, 0, 1, 2, …）传播，并且所需的时钟相位始终彼此相邻，从而允许

本文提出的2:1 多路复用器 和 (b) 其仿真结果的量子细胞自动机实现。)

正确的信号传播。如图3(a) 所示的单元结构是本文提出的多路复用器的量子细胞自动机实现，其目标是实现高器件密度、低布局面积和高计算速度。该多路复用器的仿真结果如图3(b) 所示。在双稳态近似下，采用 QCADesigner 2.0.1版本 和默认参数对 2:1 多路复用器进行了仿真和验证。

所提出的QCA 2:1多路复用器的性能在面积、时钟区域和单元复杂度方面与现有设计进行了比较，结果如表1所示。第1列表示方案。其余3列分别报告设计所需的QCA单元数量、面积开销以及时钟区域数量。从表1中的数据可以看出，本节提出的2:1多路复用器具有更少的单元数量、更小的面积以及时钟区域。

4.1. 4:1多路复用器

4:1 量子细胞自动机多路复用器的逻辑功能是，
OUT = I3·S0·S1 + I2·S0·S1 + I1·S0·S1 + I0·S0·S1
其中 I0、I1、I2、I3 为数据输入线，S0、S1 为两条选择线。本文提出的设计基于用于 2:1 多路复用器的模块。其示意图及量子细胞自动机布局如图4(a) 所示。仿真结果如图4(b) 所示。在双稳态近似下，对 4:1多路复用器进行仿真与验证，QCADesigner 2.0.1版本 中设置的参数如下：采样数 = 450,001，作用半径 = 45 nm，每样本最大迭代次数 = 1000。其余参数设为默认值。

4.2. 8:1 多路复用器

8:1 多路复用器由两个4:1多路复用器和一个2:1多路复用器组成。所有输入(I0–I7)均位于同一时钟区域，因此由全部八个输入组成的与门也处于同一时钟区域。两条选择线S0和S1控制两个4:1多路复用器，选择线S2控制2:1多路复用器。8:1多路复用器的量子细胞自动机实现如图5所示。8:1多路复用器的仿真结果如图6所示。4:1和8:1多路复用器的相对性能分析在表2 中从面积、时钟区域和单元复杂度方面进行了展示。在双稳态近似下，对8:1多路复用器进行了仿真和验证。QCADesigner 2.0.1版本中的参数设置如下：采样数 = 1,400,000，作用半径 = 41 nm，收敛容差 = 0.000000100，每采样点最大迭代次数= 1000，其余参数设为默认值。

5. 提出的多路复用器的功耗估计

量子细胞自动机（QCA）计算范式引入了具有极高速度（THz量级）的高度流水线架构。分子QCA的速度可能超过2.5 THz。理论上，处理速度可达25 THz [1]。

扭结能量在功耗估计中起着重要作用，因为它与功耗和稳态极化误差呈直接且相反的关系。因此，需要选择一个最优的扭结能量值，以在误差和功耗之间取得折衷。在此背景下，保持温度因子恒定，并再次观察量子细胞自动机单元尺寸以及相邻单元间距变化对扭结能量的影响。在[9]中提出了一个模型，用于计算具有陡峭时钟跳变的量子细胞自动机电路中的功率损耗。这会导致非绝热操作，并产生功耗上限。在[9,10]中，研究了扭结能量对量子细胞自动机电路输出误差和功耗的影响，试图在这两者之间取得折衷。本报告的目的是基于上述模型[9]，估算多路复用器电路中的功耗结果。

5.1. 多路复用器中功耗的估算

在多路复用器电路中，切换事件从一个时钟区域到另一个时钟区域期间，扭结能量变化对功耗的影响已进行了分析，结果如表4所示。可以发现，电路中的扭结能量

表1 2选1多路复用器的比较。
设计	# 单元	面积 (μm²)	时钟区域
在 [6]	41	0.08	4
在 [3]	56	0.07	4
在 [7]	36	0.06	3
在 [8]	27	0.03	3
本文提出	23	0.02	2

与整体平均功耗有直接关系。当扭结能量增加时，输出节点极化误差得到改善，但功耗恶化。

5.2. 多路复用器的输出节点极化误差

已经注意到，随着温度的升高，极化误差和功耗速率都会增加。在当前的分析中，在保持温度恒定的情况下，随着扭结能量的增加，节点极化误差减小，如（表3）所示。因此，我们可以得出结论：最大扭结能量E_k 的增加具有

表3 不同扭结能量下输出节点偏振的对比分析。
输入	2:1多路复用器的节点偏振
	E_k = 0.5 (毫电子伏特)			E_k = 1.0 (毫电子伏特)			E_k = 1.5 （毫电子伏特）
	×10⁻⁴			×10⁻⁴			×10⁻⁴
	In [4]	In [3]	本文提出	In [4]	In [3]	本文提出	在 [4]	在 [3]	本文提出
000	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
001	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
010	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
011	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
100	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
101	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
110	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85
111	4.10	6.04	4.10	11.83	17.42	11.83	19.85	29.22	19.85

对节点极化增益具有积极影响。随着设计中单元数量的增加，这种效应变得越来越显著。也就是说，两个执行相似逻辑功能但单元数量不足的设计，在输出节点可能表现出不同的极化状态。详细信息见表3。因此，E_k 的增加指的是量子点细胞大小和网格间距的减小，从而导致更紧凑的结构。

表3表明，本文提出的多路复用器实现了与[4]中相当的输出节点极化，并且相较于[3]中定义的设计有显著改进。另一方面，与 [4]（表4）中报道的设计相比，观察到较低的功耗。因此，可以得出结论：本文提出的设计不仅为高阶多路复用器的构建提供了一种模块化方法，而且在能效方面也具有较强的鲁棒性。
| 表4 不同多路复用器的功耗比较分析 | | | | | | | | | |
| — | — | — | — | — | — | — | — | — | — |
| 参数 | E_k = 0.5 （毫电子伏特） × 10⁻² | | | E_k = 1.0 （毫电子伏特） × 10⁻² | | | E_k = 1.5 （毫电子伏特） × 10⁻² | | |
| | 输入 [4] | 输入 [3] | 本文提出 | 在 [4] | 在 [3] | 本文提出 | 在 [4] | 在 [3] | 本文提出 |
| 2:1多路复用器的功耗 | | | | | | | | | |
| 电路的最大能耗 | 9.75 | 23.69 | 5.57 | 9.88 | 26.17 | 6.11 | 10.46 | 29.87 | 6.97 |
| 电路的平均能耗 | 4.20 | 13.15 | 3.03 | 5.15 | 17.46 | 4.00 | 6.41 | 22.69 | 5.20 |
| 电路的最小能耗 | 0.53 | 3.29 | 0.62 | 1.79 | 9.15 | 1.90 | 3.40 | 15.75 | 3.40 |
| 平均漏电能耗 | 0.67 | 3.40 | 0.66 | 2.11 | 9.36 | 1.99 | 3.82 | 16.00 | 3.52 |
| 平均开关能耗 | 3.52 | 9.74 | 2.37 | 3.03 | 8.10 | 2.01 | 2.58 | 6.68 | 1.68 |
| 8:1多路复用器的功耗 | | | | | | | | | |
| 电路的最大能耗 | 4.93 | 1.98 | 1.17 | 5.11 | 2.34 | 1.46 | – | 2.81 | 1.84 |
| 电路的平均能耗 | 2.59 | 1.11 | 0.70 | 3.11 | 1.61 | 1.07 | – | 2.21 | 1.51 |
| 电路的最小能耗 | 0.38 | 0.36 | 0.24 | 1.23 | 0.99 | 0.69 | – | 1.69 | 1.19 |
| 平均漏电能耗 | 0.39 | 0.37 | 0.25 | 1.25 | 1.00 | 0.70 | – | 1.70 | 1.20 |
| 平均开关能耗 | 2.20 | 0.74 | 0.45 | 1.86 | 0.61 | 0.37 | – | 0.50 | 0.31 |
| ‘–’=无法估算。 |

6. 提出的多路复用器的容错行为

纳米级电子学最重要的特性之一是与超大规模集成电路相比预期的高缺陷密度。这是由于采用了纳米级操作（如自下而上的自组装）来替代传统的基于光刻的技术所致。量子细胞自动机制造中的合成和沉积阶段是缺陷产生的主要来源。由于细胞沉积对工艺参数 [11]的变化极为敏感，研究人员已表明，量子细胞自动机电路更容易出现缺失和多余细胞缺陷，并对其功能产生显著影响。

在本文提出的工作中，使用HDLQ Verilog库[12]将多路复用器的量子细胞自动机布局转换为其等效的硬件描述语言表示。HDLQ设计工具中提供了具备故障注入能力的MV、反相器、扇出、L形导线的Verilog库。2:1多路复用器门的等效HdlQ模型如图8(a)所示。存在

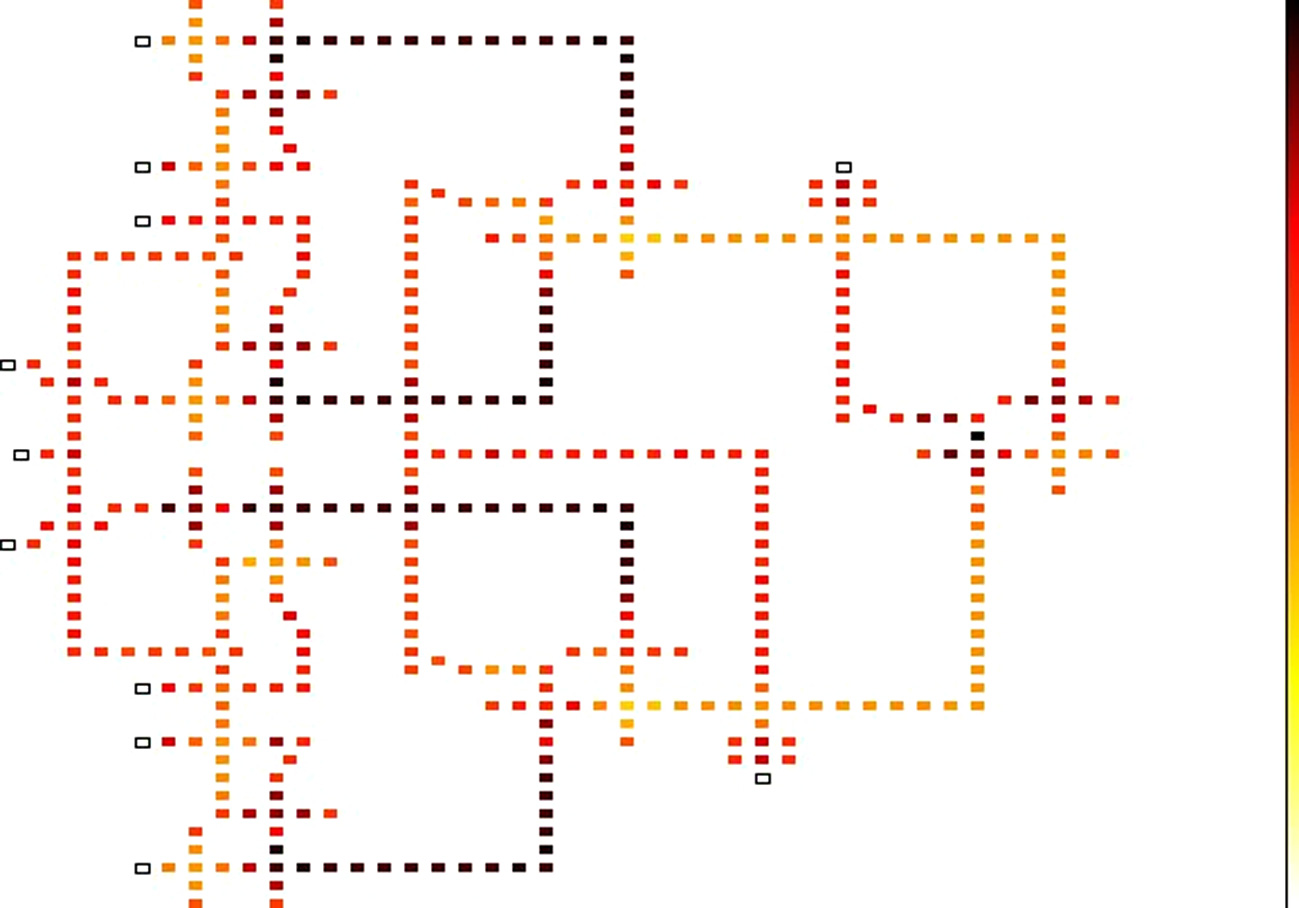本文提出的2:1多路复用器的HDLQ建模。(b) 本文提出的8:1多路复用器的HDLQ建模。)

通过使用八个输入向量测试HDLQ模型，检测到多数表决器（MAJs）、扇出（FOs）、反相器（INVs）和控制字（CWs）中所有可能的单个缺失/额外单元缺陷。在输出端生成了6种独特的故障模式，如表5所示。其中，三段模式中的十进制值以5为例，用a表示。例如，a0 代表 000（十进制0），而a7 代表 111（十进制7）。从表5可以看出，即使设计存在故障，本文提出的设计仍能平均产生77.62%的正确输出。文献[3]中报道的2:1多路复用器的容错能力为65.62%。也就是说，本文提出的2:1多路复用器比文献[3]中报道的结果提高了15.58%的容错能力。本文提出的8:1多路复用器的HDLQ模型如图8(b)所示。对该模型进行穷尽测试（考虑8个输入和3条选择线） 2¹¹，在多数表决器（MAJs）、扇出、反相器和控制字存在所有可能的单个缺失/额外单元缺陷的情况下，输出端共出现24种独特的故障模式。其平均容错能力为75.29% （由于数据量较大，未包含表格形式表示）。

7. 本文提出多路复用器的应用

在[13], FPGA中可配置逻辑块（CLB）的架构被提出。该架构支持通用多路复用，包含一个查找表（LUT）、一个触发器和多路复用器，如图9所示。为实现该架构，首先将其分解为更小的子电路，使得每个子电路均可利用单个CLB来实现。这一架构可实现多种功能

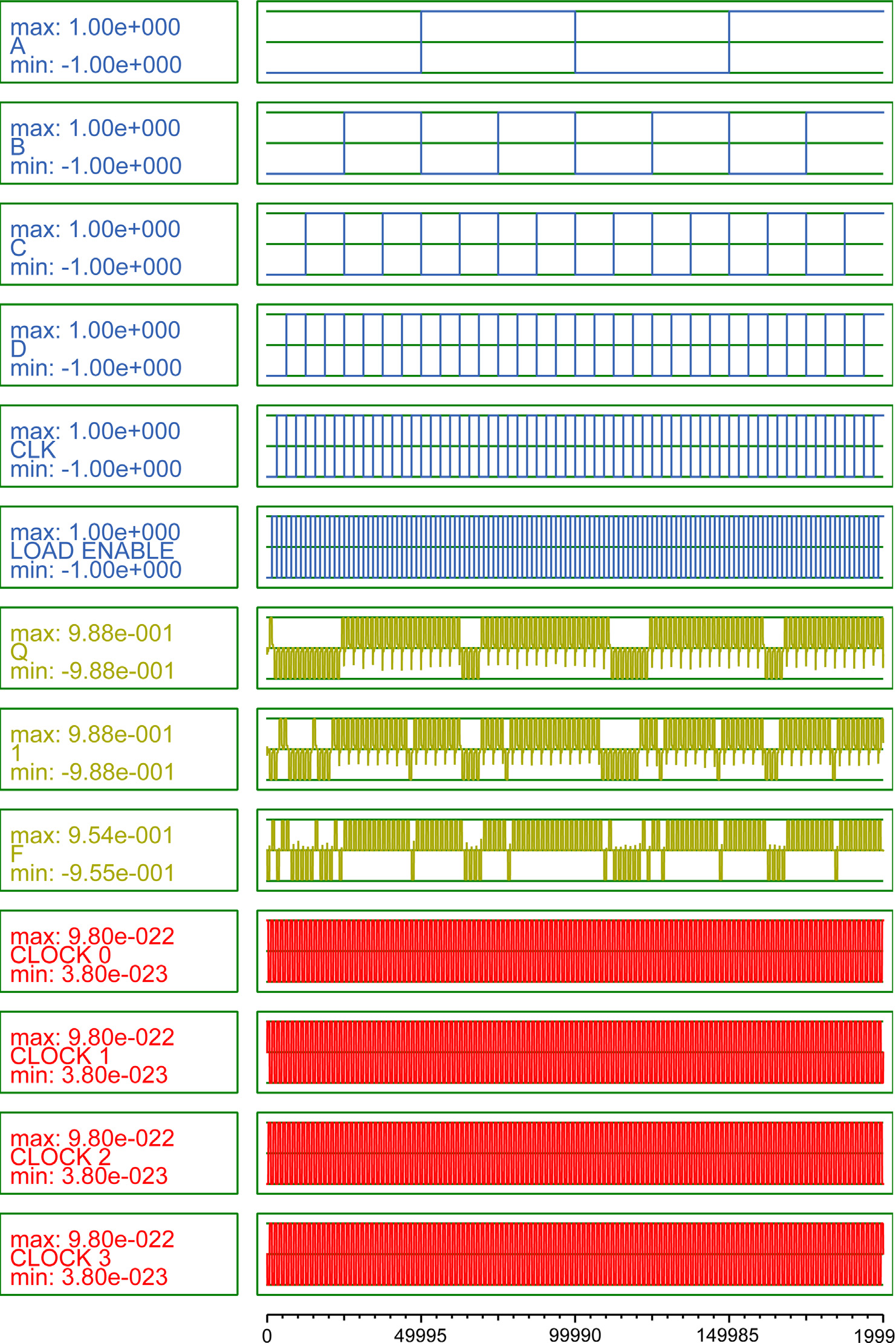
可以利用逻辑块实现，因此可配置为执行组合功能，或仅实现简单的逻辑门，如与门和异或门。CLB中的查找表可以通过解码器和存储单元实现，或通过具有掩膜常数作为输入的多路复用器实现（图10）。在本研究中，CLB单元（图10）采用量子细胞自动机技术设计（图11），并使用本文提出的2:1 多路复用器。仿真结果如图12所示。

8. 讨论

共面线路交叉会引入串扰以及增加输出节点极化误差的可能性。在给定电路中消除交叉的一种方法是复制逻辑门，从而使交叉的连接得以移除。从物理实现的角度来看，门复制不可避免地会导致面积开销。此外，使用门复制来消除线路交叉实际上会将所有交叉提前，并将其推至电路的输入端，这有效地增加了输入规模，进而增加了面积开销。在表2中显示，我们的8:1多路复用器设计的面积开销比文献[3]中报道的设计高出29%，但与[4]相比，改进显著。然而，在线路交叉方面（改善58%）以及时钟区域方面（改善 36%）也取得了显著的改进。

在量子细胞自动机结构中，最重要的方面是作用半径。作用半径决定了单元在其感应区域内相互之间作用的紧密程度。随着单元之间距离的增加，其相互影响会减弱。

表2 不同4:1和8:1多路复用器的性能比较。
设计	单元	面积 (μm²)	时钟区域	导线交叉
				4:1多路复用器	8:1 多路复用器
在 [4]	271	0.37	19	6	38
在 [3]	215	0.25	6	8	24
本文提出	155	0.24	5	3	10
改进（%）	27.9	4	16.6	62.5	58
改进 (%)					36

邻近细胞对细胞极化的影响减小。如果单元之间的中心到中心距离超过一定限度，作用半径将变为零，即邻近细胞对细胞极化不再产生影响。本文提出的设计能够正常工作的最小作用半径为28.29纳米（在2:1多路复用器中）、40.01纳米（在4:1多路复用器中）、40.01纳米（在8:1多路复用器中），而最大值没有累积点。

9. 结论

本文提出了一种利用量子细胞自动机技术设计可靠模块化多路复用器的有效方法，该方法在单元数量、时钟区域和线路交叉方面优于现有的模块化多路复用器（提升了58%）。研究探索了通过级联低阶多路复用器来模块化设计高阶多路复用器的方法。该方法通过最小化功耗和输出节点极化误差，实现了低功耗的模块化设计。同样，电路的容错能力也提高了18.25%。此外，还设计并仿真了利用该多路复用器构建可配置逻辑块（CLB）的应用。