基于QCA的极化编码电路设计

面向纳米通信网络的基于量子点细胞自动机的极化编码电路设计

摘要

基于量子点细胞自动机（QCA）的纳米通信已获得广泛的研究关注。研究人员已经报道了多种基于QCA的纳米通信架构。然而，在设计用于纳米通信的QCA架构方面仍存在广阔的研究空间。本工作探索了在此方向上极化编码器的设计与实现。极化码是一种实现可靠数据通信的技术。极化码以渐近误差指数的上界 β< 1 2 呈指数级降低块错误概率。本文展示了在纳米尺度下基于QCA的低功耗极化编码电路设计。该设计采用自下而上方法进行。同时展示了采用极化码的纳米通信架构。此外，还探讨了固定故障对生成有效极化码的影响。提出了测试向量以促进编码器电路的正确实现。所提出的测试向量有助于实现100%的故障覆盖率。所提出的极化编码器电路具有低耗散能量，通过估算能量耗散得以验证。器件面积和电路延迟表明，该极化编码电路可在纳米尺度下以更快速度运行。仿真结果证明了编码器电路的设计精度。

1. 引言

量子点细胞自动机（Quantum‐dot cellular automata， QCA）是一种在纳米尺度上超越现有范式的新兴计算技术[1–3]。QCA通过量子细胞自动机单元（QCA cell）的电荷构型或磁化来编码二进制值，并借助细胞间耦合技术实现信息处理。与互补金属氧化物半导体（CMOS）器件相比，QCA能够提供高器件密度、高集成度和高开关速度，并具有超低能量耗散的特点[4–8]。迄今为止，已有大量组合逻辑电路以及时序逻辑电路在QCA中完成了设计与实现[9–13]。此外，处理器的直接设计方法[14]以及复杂的算术电路[15,16]进一步证明了QCA作为一种有前景的纳米计算器件的高效性。与传统逻辑电路相比，QCA具有固有的移位寄存器能力，这导致QCA器件中采用循环四相时钟[17]。由于这一固有特性，QCA的设计方法与传统方法有所不同。QCA的设计方法学电路已在多项研究中被探索。为了实现高性能和高器件密度，“运动中的存储”[18]是存储方面的主要设计特征，而“导线中的逻辑”[17]则用于计算。在[19],中，基于导线长度、时钟区域宽度、浪费面积和物理反馈等参数，展示了QCA设计中与“布局=时序”相关的问题。这些参数被考虑用于高效且可靠的QCA电路设计。此外，研究人员还提出了一系列设计规则，以实现QCA中高效可靠的纳米级数字电路设计[20–22]。基于量子点细胞自动机的纳米通信已引起广泛的研究兴趣。研究人员已报道了多种基于QCA的纳米通信架构。然而，在设计基于QCA的纳米通信架构方面仍存在广阔的研究空间。本工作在此方向上探索了极化编码器的设计与实现。极化码是一种前向纠错（FEC）技术，用于实现可靠的数据通信[23–25]。极化码以渐近误差指数的上界按指数级降低块错误概率 β< 1 2 。在通信中，接收器接收到的数据可能出现“1”代替“0”或反之的情况。极化码方法在传输前向数字信息中填充冗余数据。其主要目标是当某些比特丢失时，接收器能够利用这些冗余数据重建原始信息。本文的贡献如下：

基于量子点细胞自动机的纳米尺度低功耗极化编码电路设计及其相应实现被展示。该设计采用自下而上的设计技术进行，实现采用单层方法进行。

• 还展示了具有极化编码器的纳米通信架构。

• 探讨了有效极化码生成过程中的固定故障效应。提出了测试向量以促进编码器电路的正确实现。提出的测试向量有助于实现100%的故障覆盖率。

• 所提出的极化编码电路能量耗散较低，这通过估算能量耗散得以证实。

• 器件面积和电路延迟表明，极化编码电路可在纳米尺度上以更快速度运行。

本文结构如下。第2节展示了量子点细胞自动机概述。第3节探讨了先前的工作。第4节绘制了极化编码器的构造和数据通信。第5节展示了在量子点细胞自动机中的实现。第6节演示了电路复杂性、固定故障分析和能量耗散。最后，第7节总结了研究成果。

2. 量子细胞自动机概述

标准量子细胞自动机单元由方形结构中的四个点表示，其中包含两个电子[1]。该结构如图1a所示。这些点通过隧道势垒连接，每个点可容纳一个电子。单元内的两个电子位于对角位置。二进制数字“0”和“1”由不同状态决定，如图1a所示。基本量子细胞自动机电路由具有确定构型的耦合的量子细胞自动机单元组成。反相器和多数门（MV）是量子细胞自动机的基本器件[2],，分别如图1b和c所示。

量子点细胞自动机器件单元，(b) 多数逻辑门，(c) 反相器，和 (d) 时钟 ing.)

多数门（MV）是一个三输入单输出门。最内层的单元是器件单元，其极化状态取决于相邻输入单元的多数状态。然后输出单元复制中心单元的极化状态。多数门的布尔逻辑为 M (a, b, c) = ab+ bc+ ca。当a、b、c中任意一个永久置于逻辑“0”时，多数门可实现两输入与门功能，即若c= 0，则MV(a, b, 0) = a • b，这对应于输入 a和b的逻辑与。类似地，若c = 1，则MV(a, b, 1)= a+ b，这对应于输入a和b的逻辑或。因此，利用量子细胞自动机器件可实现任意数字逻辑功能。

量子细胞自动机时钟对于实现电路的同步是必要的。一种通用的时钟方案[17,26]如图1d所示，包含四种相位，分别为松弛模式、切换模式、保持模式和释放模式。量子细胞自动机单元在切换模式开始接收数据，然后在保持模式锁存数据。随后，在释放模式中数据被释放，并进入空状态，即在松弛模式下无数据。量子细胞自动机电路被周期性地划分为四个相邻的时钟区域。每个时钟区域具有相同的时钟信号，各个信号之间依次偏移90度相位，以控制数据流。在同一时钟区域内，所有量子细胞自动机单元处于相同的相位，并同时切换。信息按照图1d中曲线箭头所示的方向流动。由于这种循环时钟方案，实现了量子细胞自动机固有的移位寄存器特性。

3. 相关工作

已有若干研究提出开发用于纳米通信的量子点细胞自动机架构 [27–39]。在 [27], 中，基于多路复用器（MUX）和多路分解器（DEMUX）的路由器架构已在量子点细胞自动机中实现，以使信道利用率达到最大值。在 [28], 中，针对纳米计算信道的计算保真度使用量子点细胞自动机（QCA）器件构成的电路在噪声信道中的性能已进行估算，该噪声信道由量子细胞自动机单元阵列组成。在测量过程中，考虑了阵列中存在的随机缺陷。与[27],相比，[29]中提出了一种利用解复用器（DEMUX）、并行输入串行输出转换器（PISO converter）和交叉开关架构的纳米路由器电路，详细描述了该纳米路由器在信息路由方面的效率。在[30],中，实现了基于QCA的4位数据处理器电路，该处理器可执行信息预处理、S形函数生成等多种多功能操作。文献[31]提出了一种能够实现串行通信的鲁棒QCA架构，该架构包含PISO转换器、汉明码生成器、奇偶校验器和串行输入并行输出转换器（SIPO converter）。在[32],中展示了涡轮编码器的设计流程及其在QCA中的实现。文献[33–37]探讨了可逆逻辑在QCA中的引入及其在纳米通信架构设计中的应用。此外，通过[38,39]提出了多种密码学与隐写术架构，以实现纳米通信过程中的安全性。

在[40],中演示了QCA中算术逻辑单元（ALU）的改进设计，该 ALU由2选1多路复用器（2:1 MUX）、双输入异或门（two‐input XOR gate）和1位全加器电路（1‐bit full adder circuit）构成，其基本操作包括与操作（AND operation）、或操作（OR operation）、异或操作（XOR operation）和加法操作（ADD operation）。在[41],中，层次化设计并实现了两种输入/输出接口——数据锁存器（data latch）和数据缓冲器（data buffer），用于实现内部和外部总线之间的数据传输，并对这两种方案进行了比较。文献 [41],还解释了如何利用这些输入/输出接口克服传统三态门存在的问题。在[42]中探索了一种高效的QCA SRAM单元实现方案，该设计包含一个三输入多数门（three‐input MV）、一个五输入多数门（five‐input MV）以及一个2选1多路复用器（2:1 MUX），并对该设计的结构强度和能效进行了精确描述。在[43],中提出了一种新颖的可编程QCA电路，该电路采用交叉开关架构设计，可用于实现任意布尔逻辑，适用于设计和仿真面积高效、稳定且一致的QCA电路。文献[44]报道了一种鲁棒且高效的同步计数器设计，该设计由D触发器和边沿到电平转换电路构成，并对其能量耗散进行了估算。相较于最新同类设计，该计数器在复杂度和能量耗散方面表现更优。为提升冯·诺依曼架构下的处理速度并降低延迟，文献[45]在QCA中实现了内存处理（Processing in Memory, PIM），并结合阿克斯阵列架构（Akers array architecture）进行了QCA实现，同时基于该QCA阿克斯阵列提出了三输入异或门（three‐input Ex‐OR gate）的实现方法。在[46]中探索了基于QCA的单层设计及新型电路交换网络（ CSN）的实现，该CSN的基本构建模块包括交叉开关、多路复用器（MUX）和解复用器（DEMUX），并演示了控制信号在通过CSN进行通信过程中的影响。所提出的各种设计功能正确，已通过仿真结果验证。在[47]中设计了一种可逆指纹认证电路，该设计采用费曼门（Feynman gate）并在QCA中实现，同时展示了使用该认证电路进行的认证过程，仿真结果证明了其设计精度。在[48],中提出了一种经优化的弗雷德金门（Fredkin gate）及其QCA实现，并进一步利用该弗雷德金门设计了一种可根据用户密码识别授权用户的认证电路。该QCA弗雷德金门相较于现有设计具有更少的单元数量、更低的延迟和更小的器件面积，同时还估算了其在热随机性条件下的计算功能，以评估电路稳定性。在[49]中阐述并实现了基于电子密码本（ECB）的分组密码QCA设计，提出了一种既能生成分组密码又能作为解码器电路工作的编码器电路。

4. 提出的纠错编码器

4.1. 极化码

极化码[23–25]是一种线性分组码，常被称为纠错码。通过递归级联短核码来构造极化码，将物理介质转换为虚拟外部介质。当递归过程次数较多时，虚拟介质将具有高可靠性（即高极化）或低可靠性（即低极化），信息比特被分配到最可靠的介质上。该码的构造旨在达到对称二进制输入离散无记忆信道（B‐DMC）的容量，并在容量差距上具有多项式依赖性。

定义1。 形式上，极化码由一个四元组（N，R，A，uA）定义，其中：

• N表示通过通信信道传输的信息比特长度，即码块长度。

• R ∈[0, 1]表示码率，即每比特中包含的数据量。

• A ⊂{1, 2, 3…, N}表示信息集，即信息比特位置的集合。

• uc A ⊂ uA表示冻结比特，即具有固定数据的比特。这里，uc A ∈{0, 1} N ( 1 − R ) 。

定义2。 极化码是一种具有K个输入和N个输出的分组码，通常称为 (N; K)极化码，其码率为(K N)。设GN为具有N比特输入和N比特输出的极化码，其中N ={1, 2, 3…, N}。再次说明，输入到GN的是以ai(i = 1, 2, . . . .., N)表示的行向量，即长度为N的行向量ai= (a1, a2, . . . , aN)，进入第i个输入端。类似地，GN的输出是以bi(i = 1, 2, . . . .., N)表示的行向量，即长度为N的行向量bi=(b1, b2, . . . , bN)，从第i个输出端输出。则GN可定义为GN=(ai; bi)，其冻结比特为ac i ∈{0, 1}N(1− K N)，即ac i ∈{0, 1}(N−K)。

4.2. 极化编码器

极化编码器的框图。)

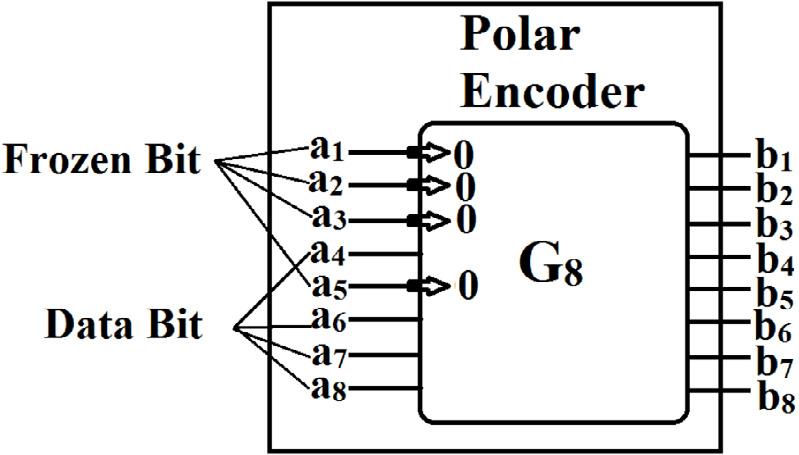
图2展示了(8;4)极化编码器，即具有4个输入和8个输出的极化编码器，用G8表示。其中，ai=(a1, a2, . . . , aN)为输入，bi=(b1, b2, . . . , bN)为输出。实际上，该编码器有8个输入，其中4个输入为冻结比特，即固定值，其余4个输入端口可用于输入数据。冻结比特的值通常固定为‘‘0’’，但也可以是其他任意值，前提是编码器和译码器均需知晓该值。在图2中，a1,a2,a3和a5为冻结比特。输入 a4, a6,a7,和a8的集合称为信息集，记作A，因为数据比特通过G8的第4、6、7和8个输入端口进行传输。A的补集记作Ac，称为冻结比特集，即冻结集。需要注意的是，信息集A的选择取决于将要进行传输的数据通信信道，不同的通信信道会产生不同类型的信息集。设n为正整数，且N =2 n。现在，对于K ≤N，可通过从{1, 2, 3…, N6,的任意K元素子集中选择信息集A来构造(N; K)极化码。但必须谨慎选择 A以获得良好的极化码。为了选择A，可以设想G8的所有输入在无冻结比特的情况下进行译码，并针对每个输入考虑其译码错误概率。这些错误概率完全依赖于通信信道(W)。因此，通过选择具有最低错误概率的A，可以获得针对通信信道(W)的最优极化码。

极化编码方案可以用包含N个节点的图来表示。该图中的层数为 (1+ log2N)。在每一层，存在N个节点。由于计算从根节点（即源层）开始，并逐层进行，因此节点总数为N ∗(1+ log2N)，即(N+ Nlog2N)，导致时间复杂度为O(Nlog2N)。

4.3. 使用极化编码器的数据通信

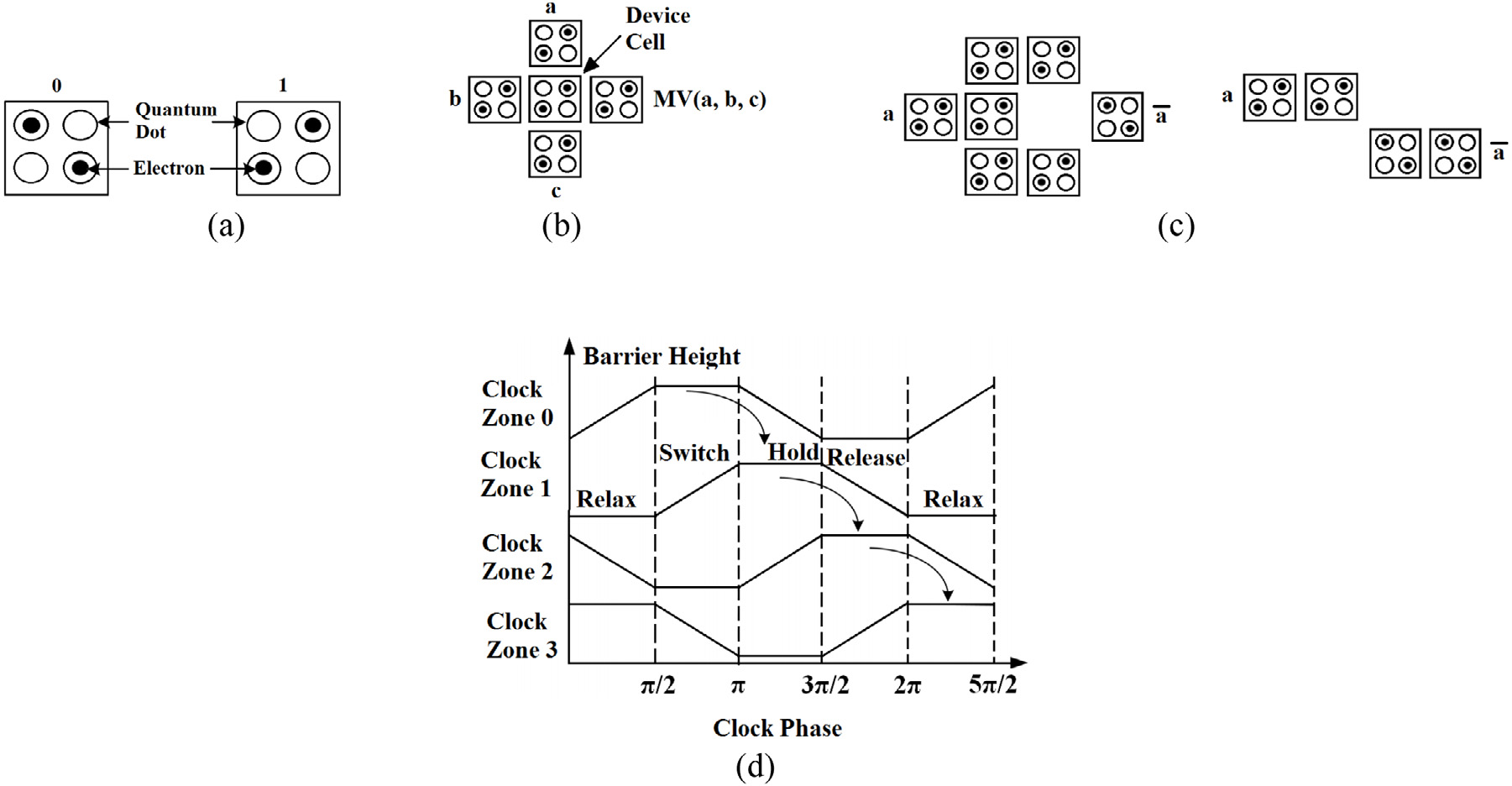
图3 展示了使用极化编码器的数据通信过程。通信按以下方式进行：

首先将选择信息集A ⊂{1, 2, 3…, N}。需要注意的是，信息集的选择取决于将要进行传输的数据通信信道，即不同的通信信道会产生不同类型的信息集。

• 现在，向量uA中存在的(N ∗ K K = K)个信息比特将与uc A中的N(1 − R)个冻结比特一起传输。

• 索引选择器将uA和uc A合并形成uN₁。

• 然后将uN₁作为输入送入极化编码器，将其变换为 xN。这里，xN = uN GN，其中GN = log N。符号表示克罗内克积。

• 现在，xN1通过通信信道（WN）进行传输。通信信道的输出为yN1。

• 在接收端，yN1将作为极化解码器的输入，该解码器对 yN1进行解码，并生成 ˆuN1，即uN1的估计值。

最后，索引选择器生成对应于 ˆuN 1的信息比特 ˆuA。

克罗内克积是一种重要的矩阵运算，支持大量快速、设计良好且实用的算法[50]。设A和B是两个矩阵，其中A ∈ℜ x1×y1，B ∈ ℜ x2×y2，且A =[a1211 a12 22] a a，B =[b123111 b12 b 13 33] 23 b b22 b b b32 b。现在，这两个矩阵A和B的克罗内克积表示为A ⊗ B，是一个x1 × y1的块矩阵，其第i行第j列的块，即(i, j)块，是一个x2×y2矩阵aijB。因此，A⊗B可推导为[50]

$$
A \otimes B =
\begin{bmatrix}
a_{11}b_{11} & a_{11}b_{12} & a_{11}b_{13} \
a_{11}b_{21} & a_{11}b_{22} & a_{11}b_{23} \
a_{11}b_{31} & a_{11}b_{32} & a_{11}b_{33}
\end{bmatrix}
\quad
\begin{bmatrix}
a_{12}b_{11} & a_{12}b_{12} & a_{12}b_{13} \
a_{12}b_{21} & a_{12}b_{22} & a_{12}b_{23} \
a_{12}b_{31} & a_{12}b_{32} & a_{12}b_{33}
\end{bmatrix}
\
\begin{bmatrix}
a_{21}b_{11} & a_{21}b_{12} & a_{21}b_{13} \
a_{21}b_{21} & a_{21}b_{22} & a_{21}b_{23} \
a_{21}b_{31} & a_{21}b_{32} & a_{21}b_{33}
\end{bmatrix}
\quad
\begin{bmatrix}
a_{22}b_{11} & a_{22}b_{12} & a_{22}b_{13} \
a_{22}b_{21} & a_{22}b_{22} & a_{22}b_{23} \
a_{22}b_{31} & a_{22}b_{32} & a_{22}b_{33}
\end{bmatrix}
$$

克罗内克积也称为直积或张量积。克罗内克积[50]的四个基本特性如下。

(1) $(A \otimes B)^T = A^T \otimes B^T$

(2) $(A \otimes B)^{-1} = A^{-1} \otimes B^{-1}$

(3) $(A \otimes B) \otimes (C \otimes D) = AC \otimes BD$

(4) $A \otimes (B \otimes C) = (A \otimes B) \otimes C$

本文主要使用克罗内克积来表示发送端模块输出x1N的值，即u1N GN，$GN=(1 0 0)^{\otimes \log_2 N}$。

4.4. GN的构造

GN可以根据简单的递归规则来定义。在本节中，已对G8进行了构造。为了获得G8,的结构，首先构造了G2。然后利用G2,的结构形成了G4。最后，通过使用G2和G4,构建了G8的结构。

4.4.1. G2的构造

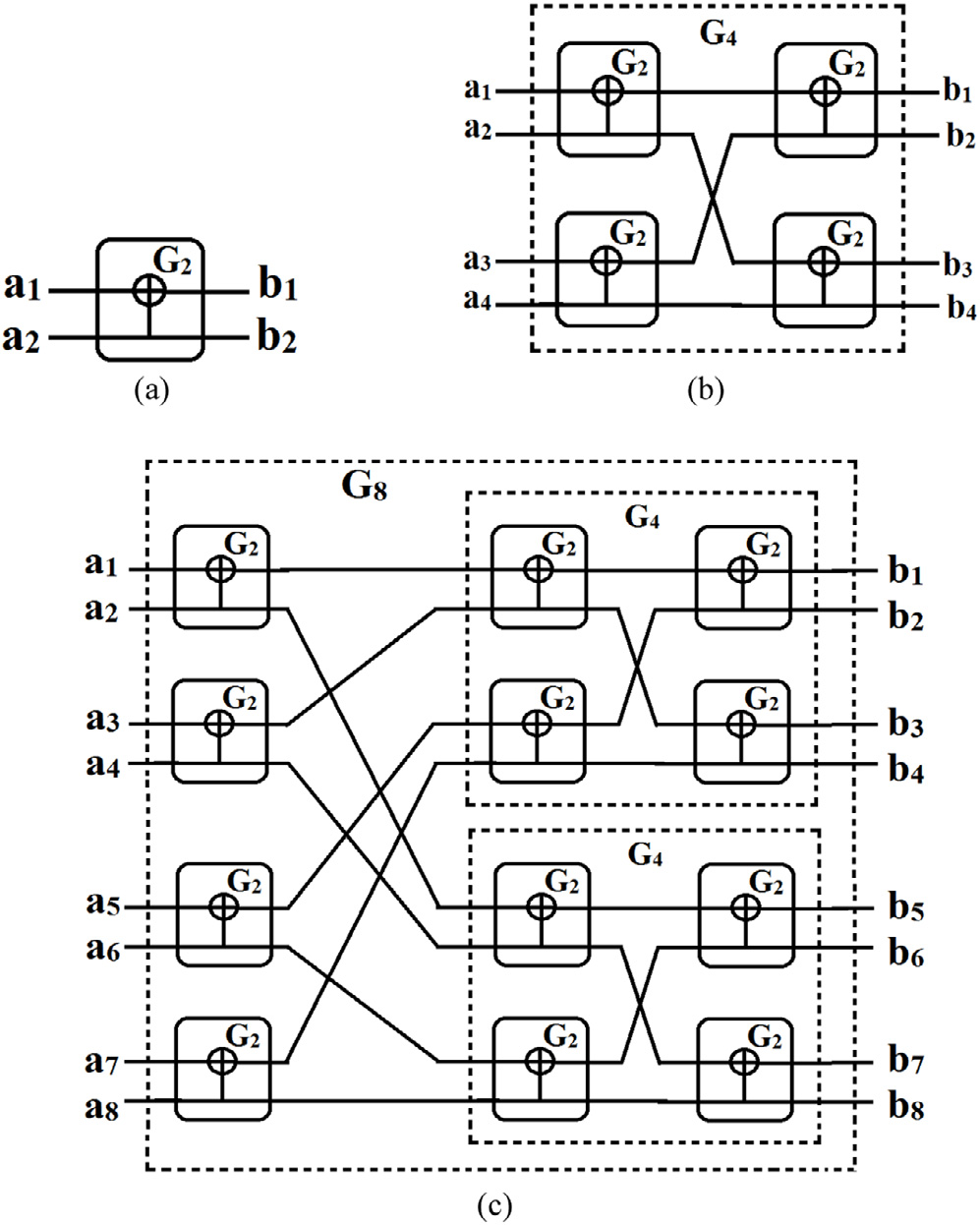
G2有两个输入（a1,a2）和两个输出（b1,b2），如图4a所示。输入‐输出映射如公式(1)和(2)所示，其中⊕表示异或操作。由(1)和(2)可以看出，输出b2与输入a2相同，输出b1是输入a1和a2的异或值。因此，仅需单个异或操作即可构建如图4a所示的G2,结构。

$$
b_1 = a_1 \oplus a_2 \tag{1}
$$
$$
b_2 = a_2 \tag{2}
$$

4.4.2. G4的构造

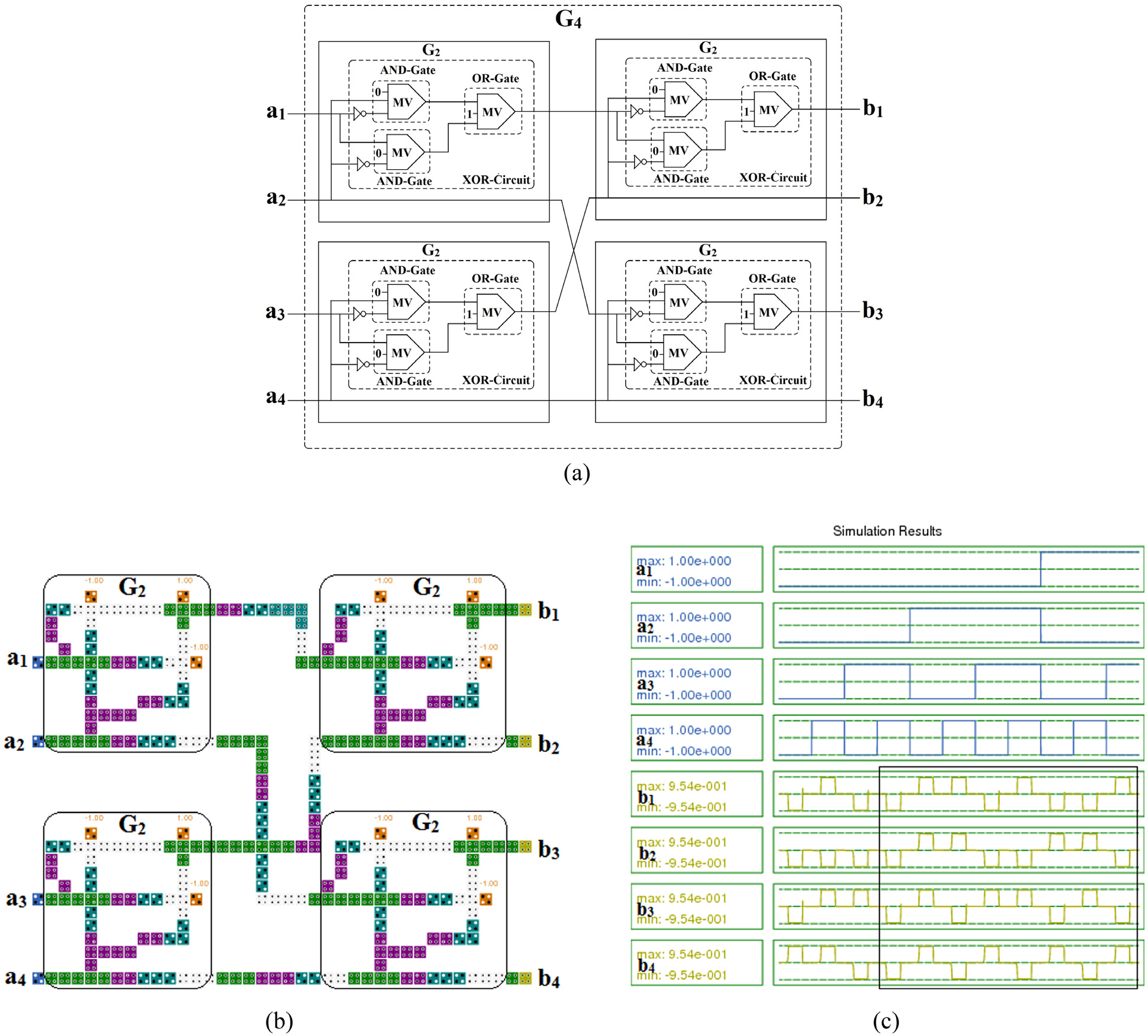
将四个 G2,副本连接起来，G4的结构可轻松构建，如 图4b 所示。从输入（a1,a2,a3,和 a4）到输出（b1, b2,b3,和 b4）的映射通过公式 (3)–(6) 给出。

$$
b_1 = a_1 \oplus a_2 \oplus a_3 \oplus a_4 \tag{3}
$$
$$
b_2 = a_3 \oplus a_4 \tag{4}
$$
$$
b_3 = a_2 \oplus a_4 \tag{5}
$$
$$
b_4 = a_4 \tag{6}
$$

4.4.3. G8的构造

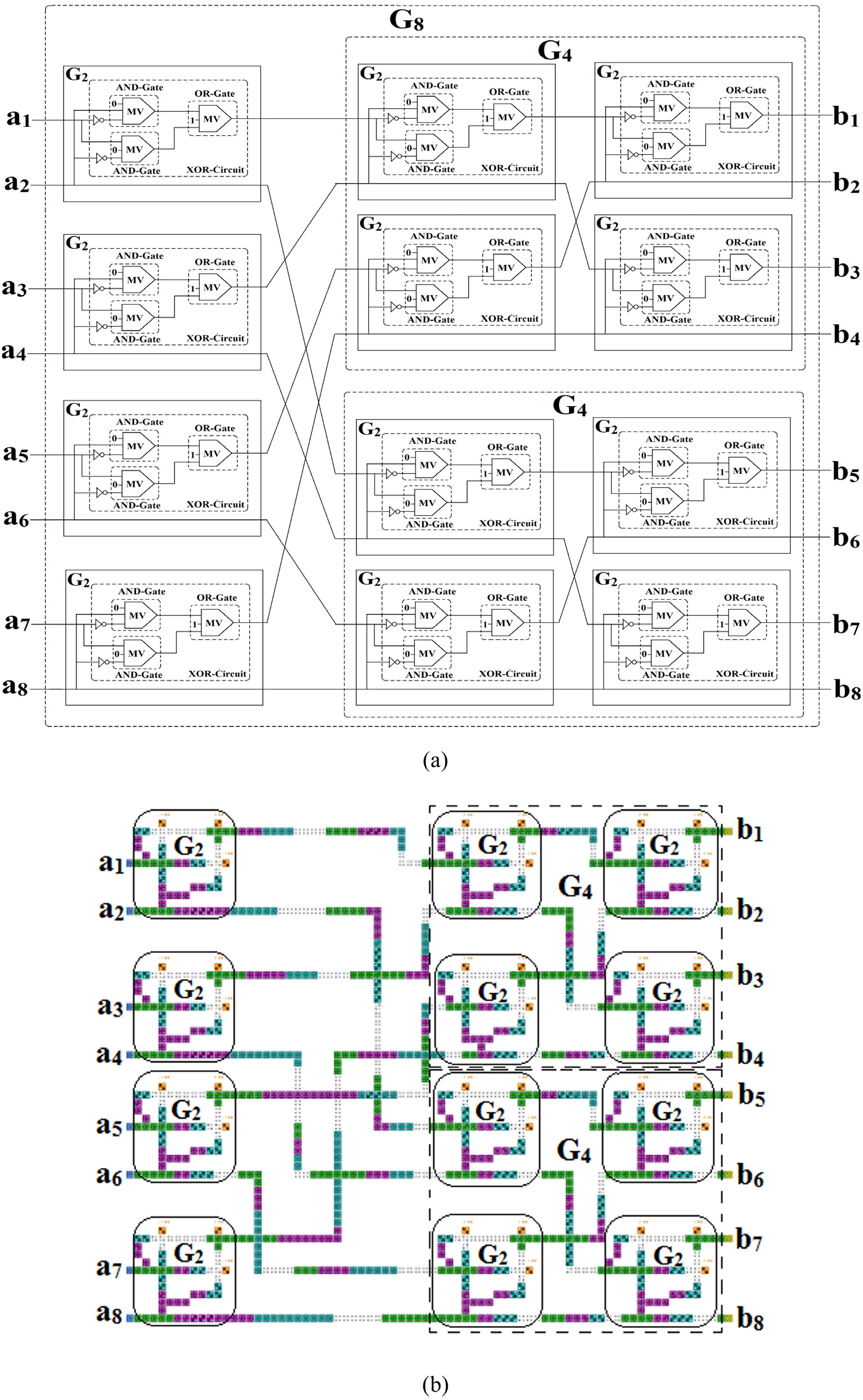
连接我们的 G2副本和两个 G4,的结构可以如 G8所示构建，如 图4c 所示。从输入ai（i= 1, 2, 3, ......, 8）到输出 bi（i= 1, 2, 3, ......, 8）的映射通过 （7）–（14）给出。

$$
b_1 = a_1 \oplus a_2 \oplus a_3 \oplus a_4 \oplus a_5 \oplus a_6 \oplus a_7 \oplus a_8 \tag{7}
$$
$$
b_2 = a_5 \oplus a_6 \oplus a_7 \oplus a_8 \tag{8}
$$
$$
b_3 = a_3 \oplus a_4 \oplus a_7 \oplus a_8 \tag{9}
$$
$$
b_4 = a_7 \oplus a_8 \tag{10}
$$
$$
b_5 = a_2 \oplus a_4 \oplus a_6 \oplus a_8 \tag{11}
$$
$$
b_6 = a_6 \oplus a_8 \tag{12}
$$
$$
b_7 = a_4 \oplus a_8 \tag{13}
$$
$$
b_8 = a_8 \tag{14}
$$

G2(b) G4和 (c) G8。)

5. 所提极化编码器的量子点细胞自动机实现

本节探讨第 4 节中构建的极化编码器的量子点细胞自动机实现。

5.1. G2的实现

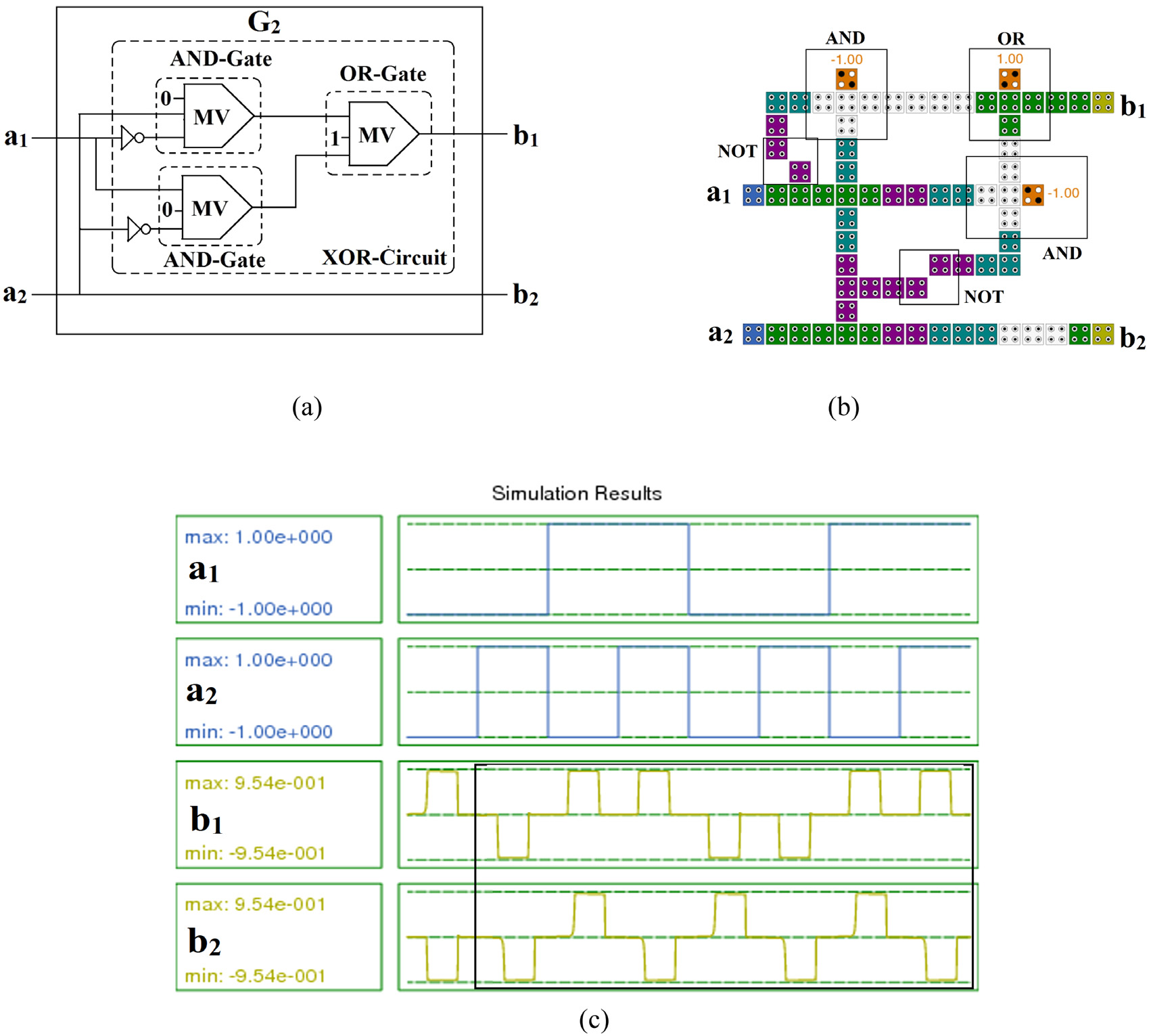
构造G2需要一个异或操作，如(1)和(2)所述。因此，一个量子细胞自动机异或电路[51,52]足以实现G2的量子点细胞自动机实现，对应于图4a，如图5a所示。图5a的量子细胞自动机布局如图5b所示。使用QCA Designer工具[53]对设计进行仿真。采用阿贝迪等人[21]提出的导线交叉技术来实现G2（图5b）。QCADesigner的四相时钟方法中两个时钟区域的优势可用于在量子点细胞自动机中实现单层导线交叉[21]。阿贝迪等人[21]证明了时钟区域0和时钟区域2可在导线交叉设计中一起使用，时钟区域1和时钟区域3同样如此。因此，为了实现所提出设计的单层结构，本文采用了基于时钟区域的实现方法 [21]。考虑采用欧拉方法与相干矢量方法执行仿真。参数如下：温度 1.0 开尔文，弛豫时间 1.0e−015秒，时间步长 1.0e−016秒，总模拟时间 7.0e−011秒，收敛容差 0.001000，样本数量 12800，时钟高电平 9.8e−22焦耳，时钟低电平 3.8e−23焦耳，时钟偏移 0.0e+000，作用半径 80 纳米，相对介电常数 12.9，时钟幅度因子 2，层间距 11.5 纳米。单元高度 20 纳米，单元宽度 20 纳米。

基于量子细胞自动机多数逻辑门的方程等效于(1)和(2)，通过(15)–(16)表示。

$$
b_2 = a_2 \tag{15}
$$
$$
b_1 = MV(MV(a_1, a_2, 0), MV(a_1, a_2, 0), 1) \tag{16}
$$

示意图，(b) 布局，和 (c) 仿真波形。)

仿真结果对应于图5b 绘制在图5c 中。矩形框用于显示有效输出。从图5c 可以看出，当a1 = 0，a2 = 0时，输出为b1 = 0和b2 = 0。当a1 = 0，a2 = 1时，输出为b1 = 1和b2 = 1。类似地，所有输出均根据输入出现。该结果与理论值一致，从而证明了设计精度。此外，从图5c 还可以看出，输出比输入延迟了一个时钟周期，即有效输出出现在第二个时钟周期。

5.2. G4的实现

构造G4需要两个G2的副本。因此，使用两个G2,的量子细胞自动机电路，可以实现对应于G4的图4b 的设计，如图6a 所示。图6a 的量子细胞自动机布局如图6b 所示。使用QCA Designer工具[53]对设计进行仿真。

示意图，(b) 布局，和 (c) 仿真波形。)

图6c显示了对应于图6b的仿真结果。矩形框用于标示有效输出。从图6c可以看出，当输入为a1= 0、a2= 0、a3= 0和a4= 0时，输出为b1= 0、b2= 0、b3= 0和b4= 0；当输入为a1= 0、a2= 0、a3= 0和a4= 1时，输出为b1= 1、b2= 1、b3= 1和b4= 1。类似地，所有输出均按照输入组合依次出现。因此，该结果与理论值一致，从而证明了设计精度。此外，从图6c还可以注意到，输出比输入延迟三个时钟周期，即有效输出出现在第四个时钟周期。

5.3. G8的实现

构造G8需要四个G2副本和两个G4副本。因此，使用四个G2的量子细胞自动机电路和两个G4 ,的量子细胞自动机电路，可实现对应于G8的量子细胞自动机电路，如图7a所示。图7a的量子细胞自动机布局如图7b所示。使用QCA Designer工具[53]对设计进行仿真。现在，如果图7b中的输入a1 , a2 , a3 , 和a5 被设置为“0”，即视为冻结比特，则其将作为(8; 4)极化编码器工作。在这种情况下，图7b中的输入a4 , a6 ,a7 ,和a8 将被视为数据位。（8; 4）极化编码器的量子细胞自动机布局如图8a所示。可以看出，图7b与图8a在结构上基本相同，仅有细微差异。图7b中的输入单元a1 , a2 ,a3 ,和a5被固定极化单元替代，即极化 = −1.0[53]因此，图7b将作为（8; 4）极化编码器工作。于是，图7b表示G8没有固定极化输入单元，而图8a表示具有四个固定极化输入单元的G（8; 4）如。

示意图，和 (b) 布局。)

(a) 布局，(b) 仿真波形。)

图8a所示的(8; 4)极化编码器对应的仿真结果在图8b中进行了描述。矩形框用于表示有效输出。图8b显示，当所有冻结比特即a1, a2,a3,和a5均设置为零时，对于数据位a4= 0、a6= 0、a7= 0、a8= 0，其输出为b1= 0、b2= 0、b3= 0、b4= 0、b5= 0、b6= 0、b7= 0和b8= 0；对于数据位a4= 0、a6= 0、a7= 0、a8= 1，其输出为b1= 1、b2= 1、b3= 1、b4=1、b5= 1、b6= 1、b7= 1和b8= 1。类似地，所有输出均根据数据位依次出现。因此，该结果符合理论值，从而证明了设计精度。此外，从图8b还可以看出，输出比输入延迟了六个时钟周期，即有效输出出现在第七个时钟周期。

6. 讨论

6.1. 提出的电路布局的复杂度

提出的QCA布局的复杂度在表1中表现优异。评估基于QCA门、器件面积、使用单元和电路延迟。可以看出，G8和G(8;4)的电路复杂度相同，但两者的固定极化QCA单元数量存在差异。G8没有固定极化输入单元，而G(8;4)有四个固定极化输入单元。此外，G8总共包含36个固定极化QCA单元，而G(8;4)总共包含40个固定极化QCA单元。

提出的QCA布局	MV数量	单元计数	固定单元数面积（µm²）	延迟（时钟周期）	固定极化QCA单元
G2	3个多数逻辑门带2个反相器	69	0.077	1.25	3
G4	12个MV带8个反相器	322	0.456	3.25	12
G8	36个中压设备配24个逆变器	1188	1.915	6.25	36
G(8;4)	36个中压设备配24个逆变器	1188	1.915	6.25	40

6.2. 固定故障效应在极化编码电路中的影响

任何基于数字逻辑门的设计都必须具备最大故障覆盖率，以实现无故障设计[54]。本节描述了所设计电路的s‐a‐0和s‐a‐1故障影响。考虑了卡在零（即“s‐a‐0”）和卡在一（即“s‐a‐1”）的故障情况。已对输入和输出端的故障进行了分析。

表2 说明了G2上的故障锁定效应。由表2 可知，如果输入a1处于 s‐a‐0状态，则对于输入‘‘10’’将生成无效代码‘‘00’’。但输入 ‘‘10’’的有效代码应为‘‘10’’。因此，通过比较输入‘‘10’’ 的有效代码和无效代码，可以检测到a1处的‘‘s‐a‐0’’故障。所以，在这种情况下， ⟨10⟩可被视为测试向量。另一方面，如果输出b1处于 s‐a‐0状态，则对于输入‘‘01’’将生成无效代码‘‘01’’。但输入 ‘‘01’’的有效代码是‘‘11’’。因此，通过比较输入‘‘01’’ 的有效代码和无效代码，可以检测到b1处的‘‘s‐a‐0’’故障。所以，在这种情况下， ⟨01⟩可被视为测试向量。以类似方式，对所有输入和输出，G2中的故障均进行了分析，并在表2中列出。对G4的故障锁定效应可执行（附录A），同样也可对G8和G(8; 4)执行故障锁定效应分析。

I/O故障类别	测试向量	有效代码	无效代码	单故障
a1 s‐a‐0	10	10	00
s‐a‐1	01	11	01
a2 s‐a‐0	01	11	00
s‐a‐1	10	10	01
b1 s‐a‐0	01	11	01
s‐a‐1	00	00	10
b2 s‐a‐0	01	11	10
s‐a‐1	10	10	11
a1a2 s‐a‐0	01	11	00	多重故障
s‐a‐1	10	10	01
b1b2 s‐a‐0	01	11	00
s‐a‐1	10	10	11

6.3. 故障覆盖率

表3显示，对于G2处的单输入/输出故障，测试向量 ⟨00,01, 10⟩具有100%的故障覆盖率。但对于G2处的多输入/输出故障，仅需测试向量 ⟨01, 10⟩即可实现100%的故障覆盖率。因此，综合来看，需要测试向量 ⟨00,01, 10⟩才能在G2处对所有单输入/输出或多输入/输出故障实现100%的故障覆盖率。另一方面，如表4所示，在G4处仅需三个测试向量 ⟨0000, 0001, 1111⟩即可实现所有单输入/输出或多输入/输出故障的100%故障覆盖率。

提出的测试向量	故障覆盖率 (%)
单故障
00	50
01	37.5
10	12.5
多重故障
00	-
01	50
10	50

提出的测试向量	故障覆盖率 (%)
单故障
0000	50
0001	25
1111	25
多重故障
0000	50
0001	25
1111	25

6.4. 能量耗散

能量估算采用汉明距离（Hd）方法[55]进行。每次的能量耗散相同量子细胞自动机单元[55,56]。每个量子细胞自动机电路的能量耗散等于量子细胞自动机设计中所有逻辑门的耗散能量之和[55]。耗散能量取决于输入到量子细胞自动机逻辑门的组合情况。量子细胞自动机器件的输入变化通过Hd来衡量。例如，当发生 0→0输入切换或 1→1输入切换时，量子细胞自动机反相器将具有Hd = 0。但对于0→1输入切换或 1→0输入切换，Hd = 1。类似地，多数逻辑门在输入切换 000→000 时将具有Hd = 0。基于这些汉明距离，多数逻辑门和反相器在[55]中进行了研究。如G2,所示，图5(b)中的提出的QCA布局包含三个多数逻辑门和两个反相器。所有多数逻辑门均有一个固定输入。因此，每个多数逻辑门具有Hd= 2。但输入至反相器的Hd值要么为零，要么为一。在不同隧穿能量（γ）和不同Hd水平下的能量耗散如表 5[55]所示。采用[55],的方法论估算了G2电路的能量耗散。为了实现最大值和最小值的能量耗散，分别考虑了Hd= 1和Hd= 0 用于量子细胞自动机反相器。

(1) 在 γ = 0.25Ek 时：

最大能量耗散 (G2max) = (3× 25.3) + (2× 28.4) = 132.7 meV.

最小能量耗散 (G2min) = (3 × 25.3) + (2 × 0.8) = 77.5 meV.

平均能量耗散 (G2avg) = (G2max + G2min) / 2 = 105.1 meV。

(2) 在 γ = 0.5Ek 时：

最大能量耗散 (G2max) = (3× 26.4) + (2× 28.6) = 136.4 meV.

最小能量耗散 (G2min) = (3 × 26.4) + (2 × 2.7) = 85.2 meV.

平均能量耗散 (G2avg) = (G2max + G2min) / 2 = 118.3 meV。

(3) 在 γ = 0.75Ek 时：

最大能量耗散 (G2max) = (3× 28.0) + (2× 29.3) = 94.6 meV。

最小能量耗散 (G2min) = (3 × 28.0) + (2 × 5.2) = 94.0 meV。

平均能量耗散 (G2avg) = (G2max + G2min) / 2 = 105.1 meV。

(4) 在 γ = 1.0Ek 时：

最大能量耗散 (G2max) = (3× 29.8) + (2× 30.2) = 149.8 meV.

最小能量耗散 (G2min) = (3 × 29.8) + (2 × 8.0) = 105.4 meV。

平均能量耗散 (G2avg) = (G2max + G2min) / 2 = 127.6 meV。

这里，Ek是扭结能量。对其他提出的QCA设计也进行了类似的估算过程。结果如图9所示。可以看出，尽管G8和G(8; 4)具有相同数量的输入和输出，G(8; 4)的耗散能量比G8低两倍。这是由于冻结比特，即G(8; 4)设计中的固定输入所致。为了更好地理解布局的耗散能量，相关结果在附录B中进行了探讨。

7. 结论

在本研究中，提出了极化编码器电路的纳米级设计及其在QCA平台上的实现。该自下而上方法已被用于降低设计复杂度。该实现是在单层中进行的，有助于在器件制造过程中降低复杂度。通信架构展示了与极化编码器的通信过程。固定故障效应分析有助于提供无故障设计。提出的测试向量足够强大，可实现100%的故障覆盖率。仿真结果证明了编码器电路的设计精度。器件面积和电路延迟表明，极化编码电路能够在纳米尺度级别以更快速度运行。所提出的极化编码电路还具有低耗散能量，这一点通过估算能量耗散得以确认。