再次深入学习深度学习|花书笔记2

再次深入学习深度学习|花书笔记2

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

---

贝叶斯

有100封邮件，其中70封是正常邮件，30封是垃圾邮件。特征“办证”在正常邮件中出现了10次，在垃圾邮件中出现了25次
计算P(X|H)，即垃圾邮件中包含“办证”的概率 P_X_given_H = 25 / 30

计算P(H)，即垃圾邮件的概率 P_H = 30 / 100

计算P(X)，即邮件中包含“办证”的概率 P_X = 35 / 100
P(H|X)=P(X|H)P(H)/P(X)=25 / 30 30 / 100 / (35 / 100)
计算P(H|X)，即包含“办证”的邮件是垃圾邮件的概率 P_H_given_X = (P_X_given_H * P_H) / P_X print(f"P(H|X) = {P_H_given_X}")

人群的发病x率是a,那么 发病x的前提下，有特征y的概率为c；有特征y的概率是b

有特征的人发病的概率 P(x|y)=P(y|x)P(x)/P(y)=bc / a
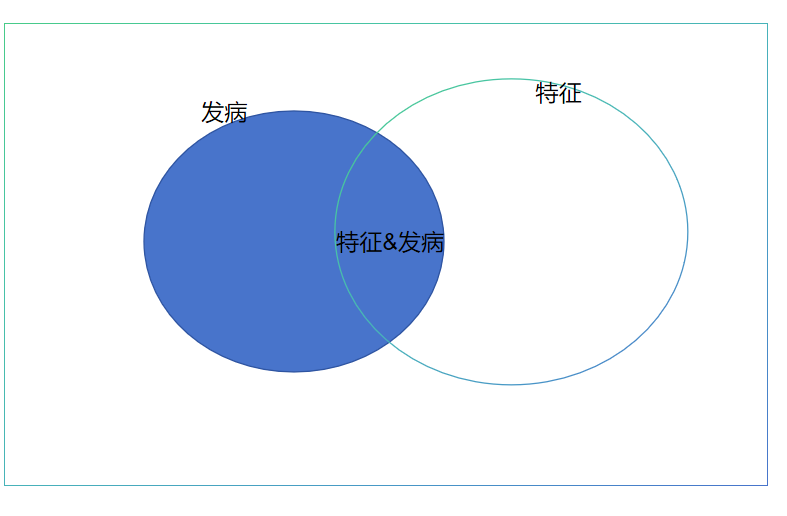
原理就是交集是相等的 ，前提是独立分布

本质上就是符合下图的这样一个特征。满足

• 有相交的区域
• 满足独立分布
  这样两个条件就行了。
  再推广，可以是多个元素的，特征A,B,C,D和发病的关系，也是同理。
  

代码

这个东西python库sklearn里面有集成的，叫高斯朴素贝叶斯方法。

最大后验估计（MAP，Maximum A Posteriori,）

相对于一般概率论喜欢的由因即果。这里是有果即因。当然，这只是一种说法。最大似然估计(MLE)和最大后验估计(MAP)本质上是一致的，最后都是求导嘛。一般，高校的概率论应该只提到了最大似然估计MLE。

最大似然估计是求θ使得似然函数**P(X|θ)最大；
最大后验概率估计是求P(X|θ)*P(θ)**函数最大，θ自己出现的先验概率也最大（其实就是考虑了参数的先验概率）。
两者的差别只在一个θ的先验概率。最后得到的东西都是θ的一个合理/期望的值。

• 加入先验概率好处在于比如硬币问题，十次里面9次都是正面，那就加入先验概率P(θ)=0.9.感觉有用，又说不上来。

花书写的这一节写得有点复杂了。

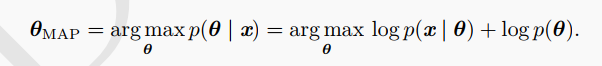
这里就是加了一个对数。
*θ = argmax P(X|θ)P(θ) = argmax(log [P(X|θ)] + log [P(θ)])

我看知乎这篇写的不错。