StandardScaler，MinMaxScaler等四个内置归一化函数学习

尊敬的组织，事情的经过是这样的：。。。。。。
自己写了一下归一化函数，跑一个线性神经网络跑出来一坨，想来想去肯定是归一化函数的问题。
还是调用方便。
sklearn.preprocessing库里面一共集成了4种Scaler方法，这个单词翻译叫定标器。

from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import MaxAbsScaler

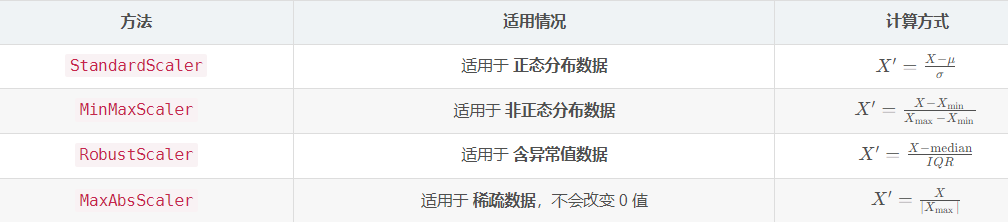
某次实验使用不同归一化函数数据

基于Max_min归一化：

**************************************************
模型评估指标:
平均绝对误差 (MAE): 42.4816
均方误差 (MSE): 3853.2547
中值绝对误差 (MedAE): 22.8512
可解释方差值 (Explained Variance Score): 0.9893
R方值 (R² Score): 0.9891

基于Stand归一化：

**************************************************
模型评估指标:
平均绝对误差 (MAE): 37.6559
均方误差 (MSE): 3362.8448
中值绝对误差 (MedAE): 24.0749
可解释方差值 (Explained Variance Score): 0.9905
R方值 (R² Score): 0.9905

基于Robust归一化：

爆炸了，压根就没拟合
**************************************************
模型评估指标:
平均绝对误差 (MAE): 443.5110
均方误差 (MSE): 441783.8972
中值绝对误差 (MedAE): 216.5900
可解释方差值 (Explained Variance Score): 0.0000
R方值 (R² Score): -0.2528

基于Max_min归一化：

**************************************************
模型评估指标:
平均绝对误差 (MAE): 45.0075
均方误差 (MSE): 4169.0116
中值绝对误差 (MedAE): 30.7425
可解释方差值 (Explained Variance Score): 0.9888
R方值 (R² Score): 0.9882

归一化

我们知道归一化，就像是跑图像的时候，先除以255，再给个方差，平均数矩阵，再甩给函数就成了。
简单的理解就是不能让e^6 和 e^-1 两个数量级的东西作为不同的特征一起去计算。
[1000,0.1,2] 这三个特征显然是有注意力差异的。这点可以通过注意力机制去理解，注意力机制就是特征*一个注意力矩阵，再去计算下一层嘛。
粗浅的估计就是一个x_scaler = (x -u)/sita .减去平均数，除以标准差，如果没有记错就是标准正态了吧。

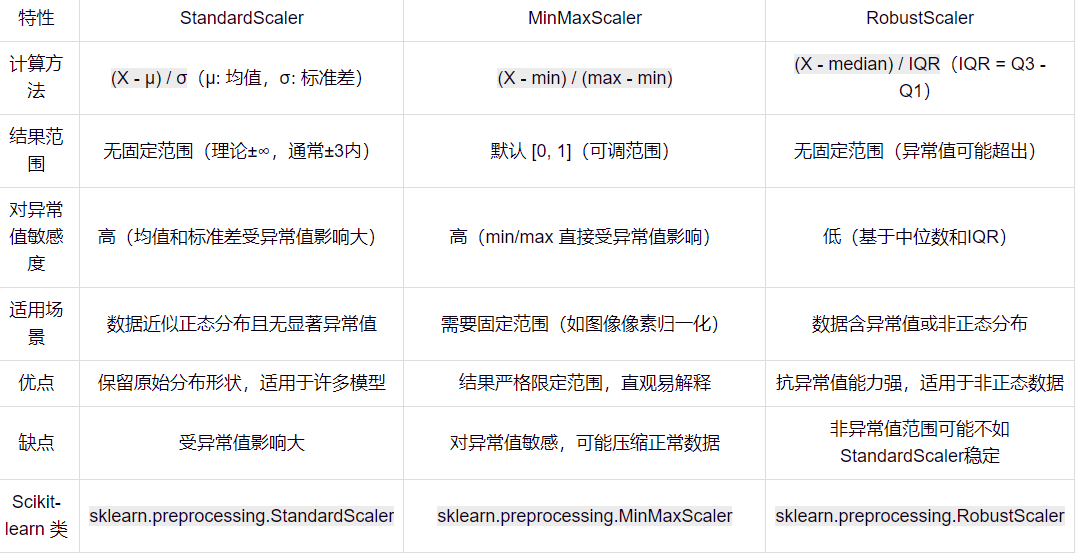
StandardScaler 和 MinMaxScaler

参考https://baijiahao.baidu.com/s?id=1825808807439588177这一篇写得很好。
就实操而言，StandardScaler 明显更好。用MinMaxScaler有时候会出问题。
它不会像魔法那样改变数据分布。就像你把一个面团擀成不同形状，虽然面团大小（尺度）发生变化，但面团原本的形状（分布）依然保留。它只是将数据“尺度”调整，使数据在模型训练时更加稳定。可以将 StandardScaler 理解为给数据换上统一战袍，让数据不因尺度差异而干扰模型学习，而能专注于特征本身规律。这样一来，模型处理数据时不再遇到天差地别的量级问题，训练过程更高效，预测结果也更加可靠。希望这个解释能帮助你对两种标准化方法有更深入理解和清晰认识。

StandardScaler

StandardScaler 就像一位精准的裁判，把数据的均值调整为 0，标准差调整为 1，适合数据服从正态分布的情况。想象参加跑步比赛，每个选手起点都设置在相同的水平线上，赛道长度也完全一致，这样大家都能公平竞争。StandardScaler 就是给数据设定统一标准，让每个数据点站在同一条起跑线上。

MinMaxScaler

MinMaxScaler 则像一位热衷于量化的教练，把所有数据拉伸或压缩到 [0,1] 或 [-1,1] 范围内，适合没有明显分布特征的数据。可以把它想象成一位严格的裁判，强迫每个选手的成绩都必须处于某个范围内，无论你跑得快或慢，成绩都必须在规定范围内。这种方式使得不同选手成绩易于比较，但它并不关注选手的实际表现，只关注排名情况。

理解源码

遇事不决研究源码。想不懂就拿代码来说话吧。

class StandardScaler(_OneToOneFeatureMixin, TransformerMixin, BaseEstimator):
    """Standardize features by removing the mean and scaling to unit variance.

    The standard score of a sample `x` is calculated as:

        z = (x - u) / s

    where `u` is the mean of the training samples or zero if `with_mean=False`,
    and `s` is the standard deviation of the training samples or one if
    `with_std=False`.

    Centering and scaling happen independently on each feature by computing
    the relevant statistics on the samples in the training set. Mean and
    standard deviation are then stored to be used on later data using
    :meth:`transform`.

    Standardization of a dataset is a common requirement for many
    machine learning estimators: they might behave badly if the
    individual features do not more or less look like standard normally
    distributed data (e.g. Gaussian with 0 mean and unit variance).

    For instance many elements used in the objective function of
    a learning algorithm (such as the RBF kernel of Support Vector
    Machines or the L1 and L2 regularizers of linear models) assume that
    all features are centered around 0 and have variance in the same
    order. If a feature has a variance that is orders of magnitude larger
    that others, it might dominate the objective function and make the
    estimator unable to learn from other features correctly as expected.

    This scaler can also be applied to sparse CSR or CSC matrices by passing
    `with_mean=False` to avoid breaking the sparsity structure of the data.

    Read more in the :ref:`User Guide <preprocessing_scaler>`.

    Parameters
    ----------
    copy : bool, default=True
        If False, try to avoid a copy and do inplace scaling instead.
        This is not guaranteed to always work inplace; e.g. if the data is
        not a NumPy array or scipy.sparse CSR matrix, a copy may still be
        returned.

    with_mean : bool, default=True
        If True, center the data before scaling.
        This does not work (and will raise an exception) when attempted on
        sparse matrices, because centering them entails building a dense
        matrix which in common use cases is likely to be too large to fit in
        memory.

    with_std : bool, default=True
        If True, scale the data to unit variance (or equivalently,
        unit standard deviation).

    Attributes
    ----------
    scale_ : ndarray of shape (n_features,) or None
        Per feature relative scaling of the data to achieve zero mean and unit
        variance. Generally this is calculated using `np.sqrt(var_)`. If a
        variance is zero, we can't achieve unit variance, and the data is left
        as-is, giving a scaling factor of 1. `scale_` is equal to `None`
        when `with_std=False`.

        .. versionadded:: 0.17
           *scale_*

    mean_ : ndarray of shape (n_features,) or None
        The mean value for each feature in the training set.
        Equal to ``None`` when ``with_mean=False``.

    var_ : ndarray of shape (n_features,) or None
        The variance for each feature in the training set. Used to compute
        `scale_`. Equal to ``None`` when ``with_std=False``.

    n_features_in_ : int
        Number of features seen during :term:`fit`.

        .. versionadded:: 0.24

    feature_names_in_ : ndarray of shape (`n_features_in_`,)
        Names of features seen during :term:`fit`. Defined only when `X`
        has feature names that are all strings.

        .. versionadded:: 1.0

    n_samples_seen_ : int or ndarray of shape (n_features,)
        The number of samples processed by the estimator for each feature.
        If there are no missing samples, the ``n_samples_seen`` will be an
        integer, otherwise it will be an array of dtype int. If
        `sample_weights` are used it will be a float (if no missing data)
        or an array of dtype float that sums the weights seen so far.
        Will be reset on new calls to fit, but increments across
        ``partial_fit`` calls.

    See Also
    --------
    scale : Equivalent function without the estimator API.

    :class:`~sklearn.decomposition.PCA` : Further removes the linear
        correlation across features with 'whiten=True'.

    Notes
    -----
    NaNs are treated as missing values: disregarded in fit, and maintained in
    transform.

    We use a biased estimator for the standard deviation, equivalent to
    `numpy.std(x, ddof=0)`. Note that the choice of `ddof` is unlikely to
    affect model performance.

    For a comparison of the different scalers, transformers, and normalizers,
    see :ref:`examples/preprocessing/plot_all_scaling.py
    <sphx_glr_auto_examples_preprocessing_plot_all_scaling.py>`.

    Examples
    --------
    >>> from sklearn.preprocessing import StandardScaler
    >>> data = [[0, 0], [0, 0], [1, 1], [1, 1]]
    >>> scaler = StandardScaler()
    >>> print(scaler.fit(data))
    StandardScaler()
    >>> print(scaler.mean_)
    [0.5 0.5]
    >>> print(scaler.transform(data))
    [[-1. -1.]
     [-1. -1.]
     [ 1.  1.]
     [ 1.  1.]]
    >>> print(scaler.transform([[2, 2]]))
    [[3. 3.]]
    """

    def __init__(self, *, copy=True, with_mean=True, with_std=True):
        self.with_mean = with_mean
        self.with_std = with_std
        self.copy = copy

    def _reset