文章目录
1 最大似然估计(MLE)
MLE就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值的计算过程。直白来讲,就是给定了一定的数据,假定知道数据是从某种分布中随机抽取出来的,但是不知道这个分布具体的参数值,即 “模型已定,参数未 知” ,MLE就可以用来估计模型的参数。MLE的目标是找出一组参数(模型中的参数),使得模型产出观察数据的概率最大。
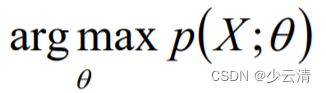
1.1 MLE求解过程
- 编写似然函数(即联合概率函数)<似然函数:在样本固定的情况下,样本出现的概率与参数θ之间的函数;
- 对似然函数取对数,并整理;(一般都进行)
- 求导数;
- 解似然方程。
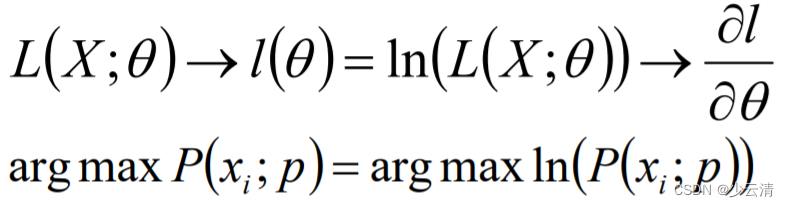
1.2 MLE案例
- 盒子中只有黑球和白球,假定白球的比例为p,那么黑球的比例为1-p。因为采取的是有放回的随机抽取,那么每次抽取出来的球的颜色服从同一独立分布情况,即每次抽取之间是独立互不影响的。
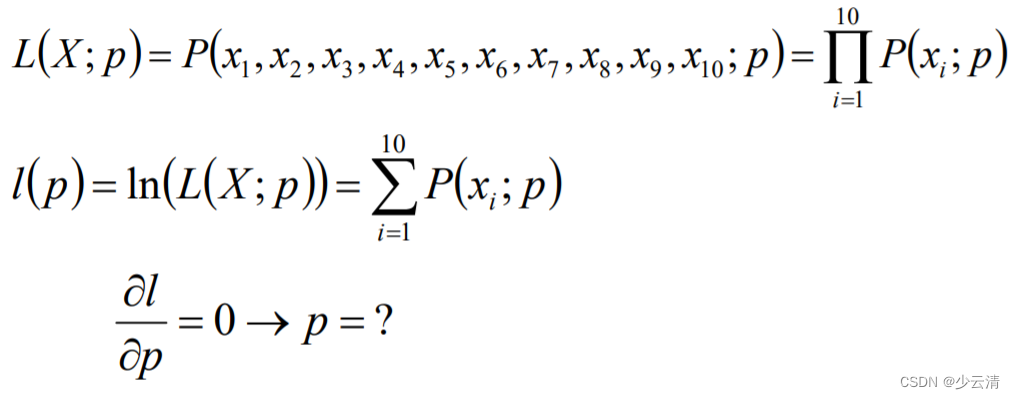

2 贝叶斯算法估计
贝叶斯算法估计是一种从先验概率和样本分布情况来计算后验概率的一种方式。
贝叶斯算法中的常见概念:
- P(A)是事件A的先验概率或者边缘概率;
- P(A|B)是已知B发生后A发生的条件概率,也称为A的后验概率;
- P(B|A)是已知A发生后B发生的条件概率,也称为B的后验概率;
- P(B)是事件B的先验概率或者边缘概率。
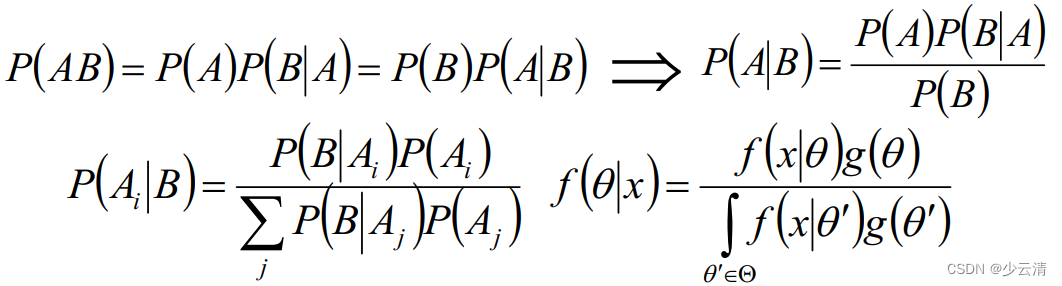
2.1 贝叶斯算法估计—案例
- 现在有五个盒子,假定每个盒子中都有黑白两种球,并且黑白球的比例如下;现已知从这五个盒子中的任意一个盒子中有放回的抽取两个球,且均为白球,问这两个球是从哪个盒子中抽取出来的?

- 现在不是从五个盒子中任选一个盒子进行抽取,而是按照一定的概率选择对应的盒子,概率如下。假定抽出白球为事件B,从第i个盒子中抽取为事件Ai。结论是从第四个盒子抽取的球

2.2 最大后验概率估计(MAP)
- MAP(Maximum a posteriori estimation)和MLE一样,都是通过样本估计参数θ的值;在MLE中,是使似然函数P(x|θ)最大的时候参数θ的值,MLE中假设先验概率是一个等值的;而在MAP中,则是求θ使P(x|θ)P(θ)的值最大,这也就是要求θ值不仅仅是让似然函数最大,同时要求θ本身出现的先验概率也得比较大。
- 可以认为MAP是贝叶斯算法的一种应用。
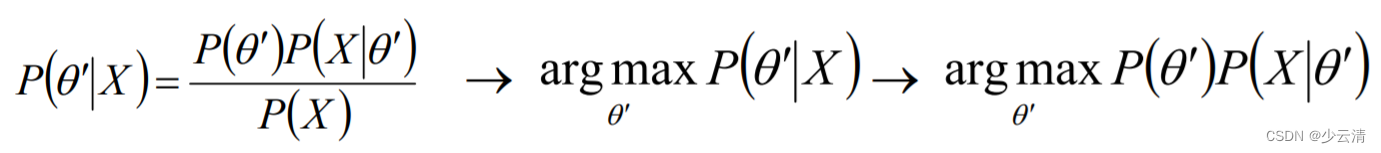
3 K-means算法

4 EM算法
EM算法(Expectation Maximization Algorithm, 最大期望算法)是一种迭代类型的算法,是一种在概率模型中寻找参数最大似然估计或者最大后验估计的算法, 其中概率模型依赖于无法观测的隐藏变量。
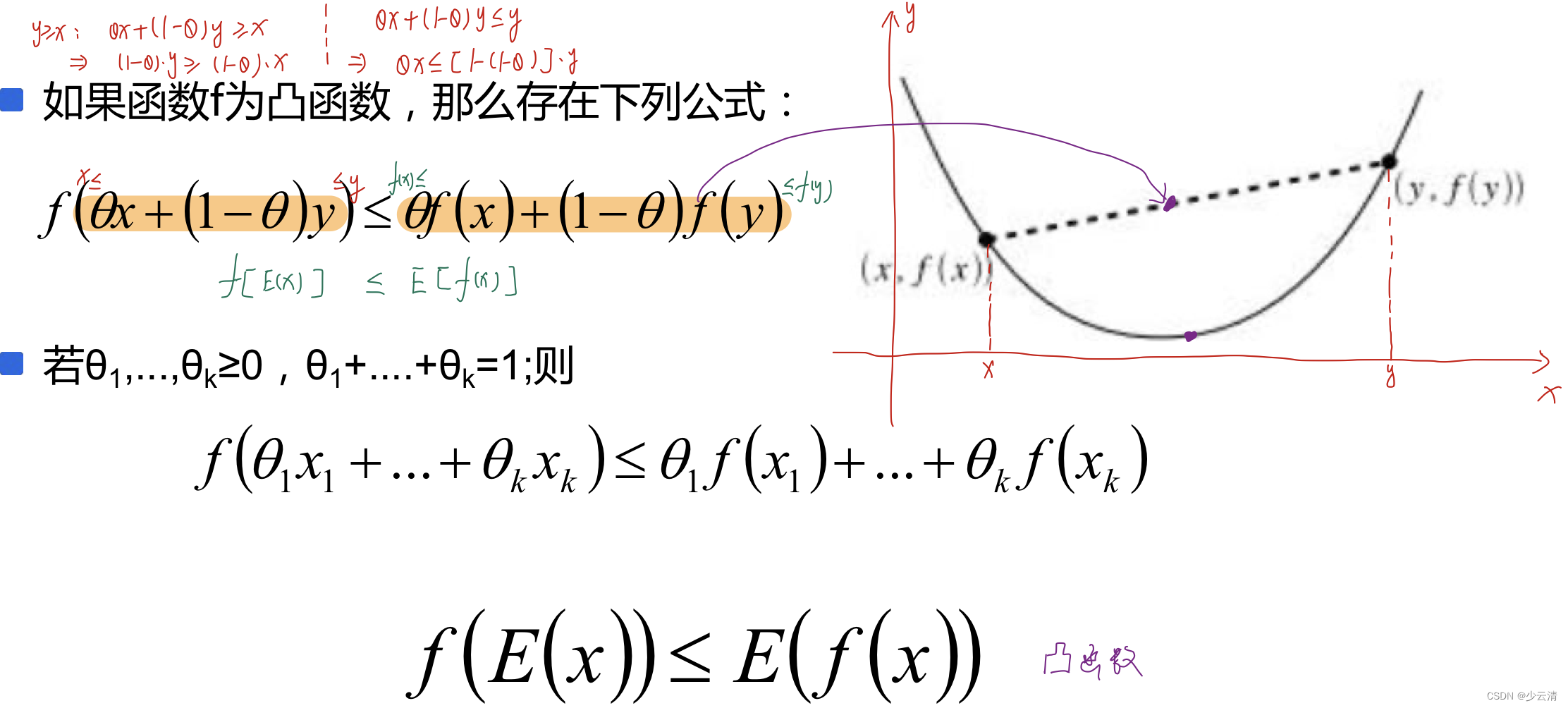
4.1 Jensen不等式
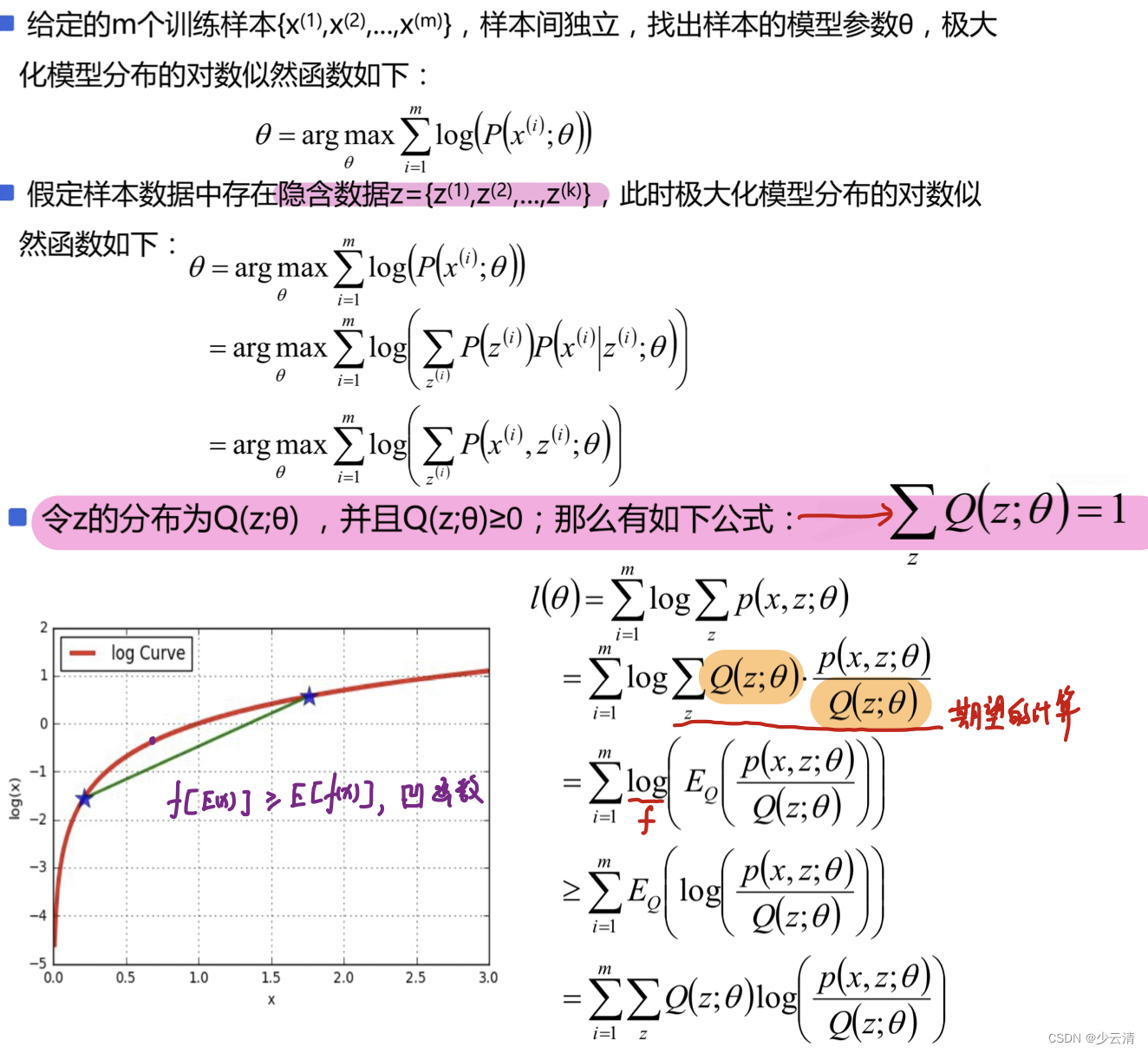
4.2 EM算法原理

4.3 EM算法流程
- 初始化分布参数/模型参数。
- 重复下列两个操作直到收敛:
- E步骤:估计隐藏变量的概率分布期望函数;
- M步骤:根据期望函数重新估计分布参数。

4.4 EM算法直观案例
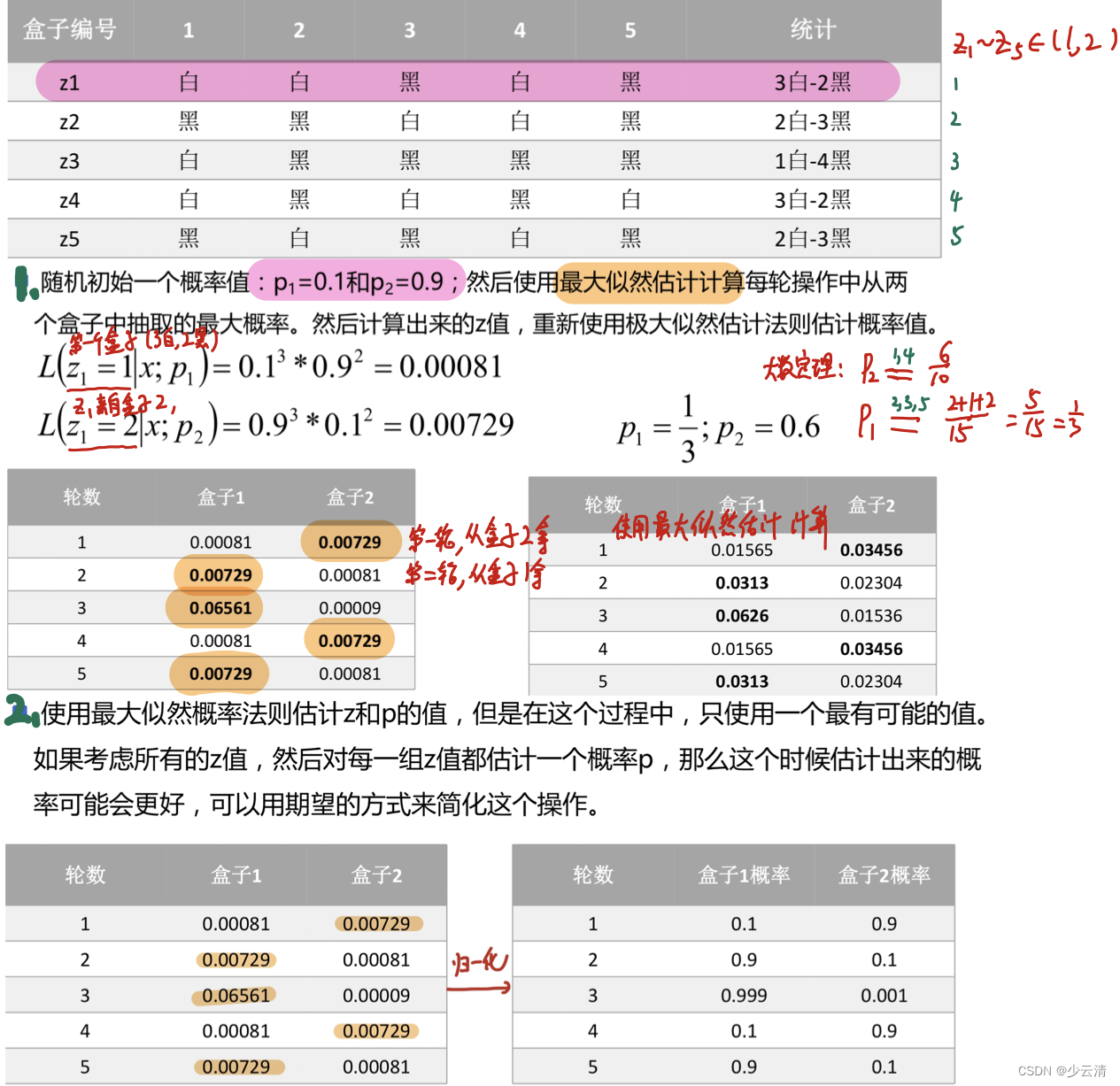
- 假设现有两个装有不定数量黑球、白球的盒子,随机从盒子中抽取出一个白球的概率分布为p1和p2;为了估计这两个概率,每次选择一个盒子,有放回的连续随机抽取5个球,记录如下:

- 假设现有两个装有不定数量黑球、白球的盒子,随机从盒子中抽取出一个白球的概率分布为p1和p2;如果现在不知道具体的盒子编号,但是同样还是为了求解p1和p2的值,这个时候就相当于多了一个隐藏变量z, z表示的是每次抽取的时候选择的盒子编号,比如z1就表示第一次抽取的时候选择的是盒子1还是盒子2。

4.5 EM算法收敛证明
- EM算法的收敛性只要我们能够证明对数似然函数的值在迭代的过程中是增加的即可

4.6 问题
随机选择1000名用户,测量用户的身高;若样本中存在男性和女性,身高分别服从高斯分布N(μ1 ,σ1 )和N(μ2 ,σ2 )的分布,试估计参数:μ1 ,σ1 ,μ2 ,σ2 ;
- 如果明确的知道样本的情况(即男性和女性数据是分开的),那么我们使用极大似然估计来估计这个参数值。
- 如果样本是混合而成的,不能明确的区分开,那么就没法直接使用极大似然估计来进行参数的估计啦,像这样存在隐变量的模型参数求解就需要用到EM算法求解。
5 GMM算法
- GMM(Gaussian Mixture Model, 高斯混合模型)是指该算法由多个高斯模型线性叠加混合而成。每个高斯模型称之为component。GMM算法描述的是数据的本身存在的一种分布。
- GMM算法常用于聚类应用中,component的个数就可以认为是类别的数量。
- 假定GMM由k个Gaussian分布线性叠加而成,那么概率密度函数如下:
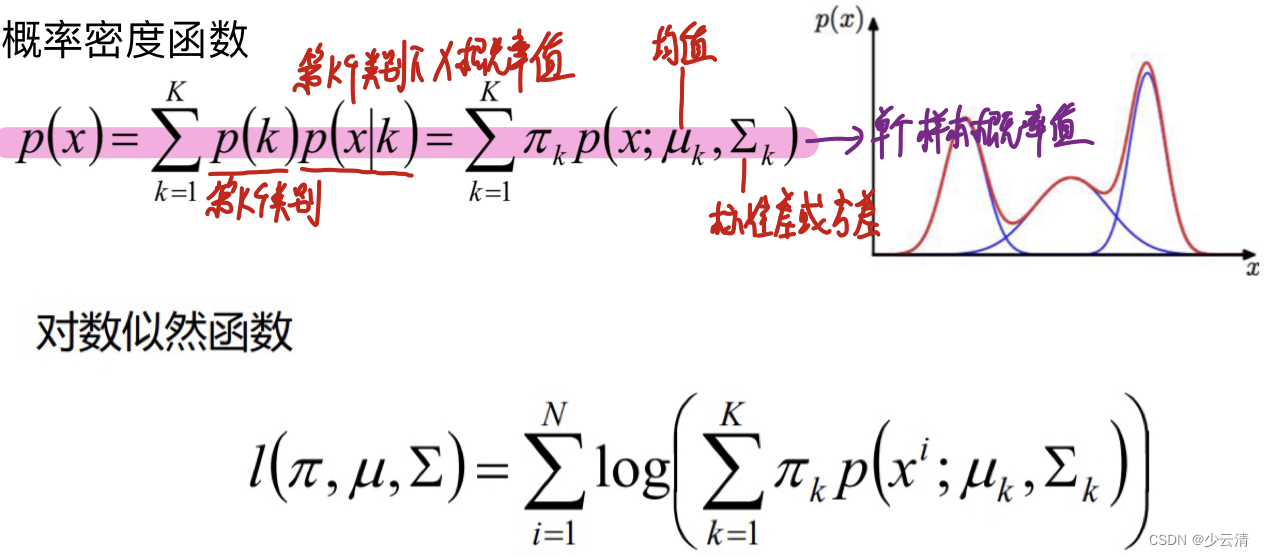
5.1 GMM-EM算法求解
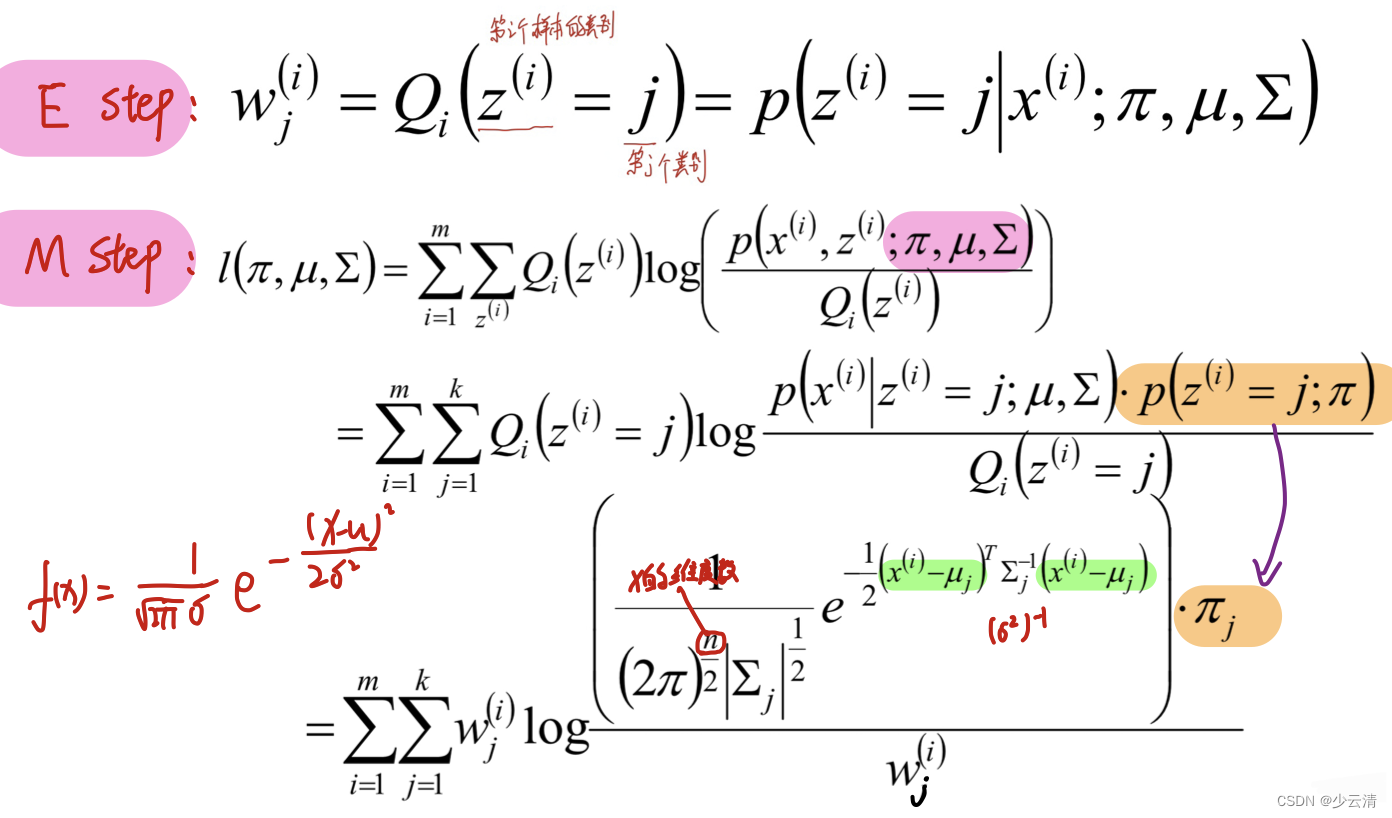


5.2 基于python的GMM高斯混合代码实现
# --encoding:utf-8 --
"""
实现GMM高斯混合聚类
根据EM算法流程实现这个流程
http://scipy.github.io/devdocs/generated/scipy.stats.multivariate_normal.html#scipy.stats.multivariate_normal
"""
import numpy as np
from scipy.stats import multivariate_normal
def train(x, max_iter=100):
"""
进行GMM模型训练,并返回对应的μ和σ的值(假定x数据中的簇类别数目为2)
:param x: 输入的特征矩阵x
:param max_iter: 最大的迭代次数
:return: 返回一个五元组(pi, μ1, μ2,σ1,σ2)
"""
# 1. 获取样本的数量m以及特征维度n
m, n = np.shape(x)
# 2. 初始化相关变量
# 以每一列中的最小值作为mu1,mu1中的元素数目就是列的数目(n)个
mu1 = x.min(axis=0)
mu2 = x.max(axis=0)
sigma1 = np.identity(n)
sigma2 = np.identity(n)
pi = 0.5
# 3. 实现EM算法
for i in range(max_iter):
# a. 初始化多元高斯分布(初始化两个多元高斯混合概率密度函数)
norm1 = multivariate_normal(mu1, sigma1)
norm2 = multivariate_normal(mu2, sigma2)
# E step
# 计算所有样本数据在norm1和norm2中的概率
tau1 = pi * norm1.pdf(x)
tau2 = (1 - pi) * norm2.pdf(x)
# 概率做一个归一化操作
w = tau1 / (tau1 + tau2)
# M step
mu1 = np.dot(w, x) / np.sum(w)
mu2 = np.dot(1 - w, x) / np.sum(1 - w)
sigma1 = np.dot(w * (x - mu1).T, (x - mu1)) / np.sum(w)
sigma2 = np.dot((1 - w) * (x - mu2).T, (x - mu2)) / np.sum(1 - w)
pi = np.sum(w) / m
# 返回最终解
return (pi, mu1, mu2, sigma1, sigma2)
if __name__ == '__main__':
np.random.seed(28)
# 产生一个服从多元高斯分布的数据(标准正态分布的多元高斯数据)
mean1 = (0, 0, 0) # x1\x2\x3的数据分布都是服从正态分布的,同时均值均为0
cov1 = np.diag((1, 1, 1))
data1 = np.random.multivariate_normal(mean=mean1, cov=cov1, size=500)
# 产生一个数据分布不均衡
mean2 = (2, 2, 3)
cov2 = np.array([[1, 1, 3], [1, 2, 1], [0, 0, 1]])
data2 = np.random.multivariate_normal(mean=mean2, cov=cov2, size=200)
# 合并两个数据
data = np.vstack((data1, data2))
pi, mu1, mu2, sigma1, sigma2 = train(data, 100)
print("第一个类别的相关参数:")
print(mu1)
print(sigma1)
print("第二个类别的相关参数:")
print(mu2)
print(sigma2)
print("预测样本属于那个类别(概率越大就是那个类别):")
norm1 = multivariate_normal(mu1, sigma1)
norm2 = multivariate_normal(mu2, sigma2)
x = np.array([0, 1, 0])
print(pi * norm1.pdf(x)) # 属于类别1的概率为:0.0275 =>0.0275/( 0.0275+0.0003)=0.989
print((1 - pi) * norm2.pdf(x))# 属于类别1的概率为:0.0003 => 0.011























 3612
3612

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










