C++带状矩阵求解：LAPACKE_dgbsv

官方文档：LAPACKE_dgbsv

作用：用于求解带状矩阵方程，已知带状矩阵A，向量B，求解x。

案例如下：

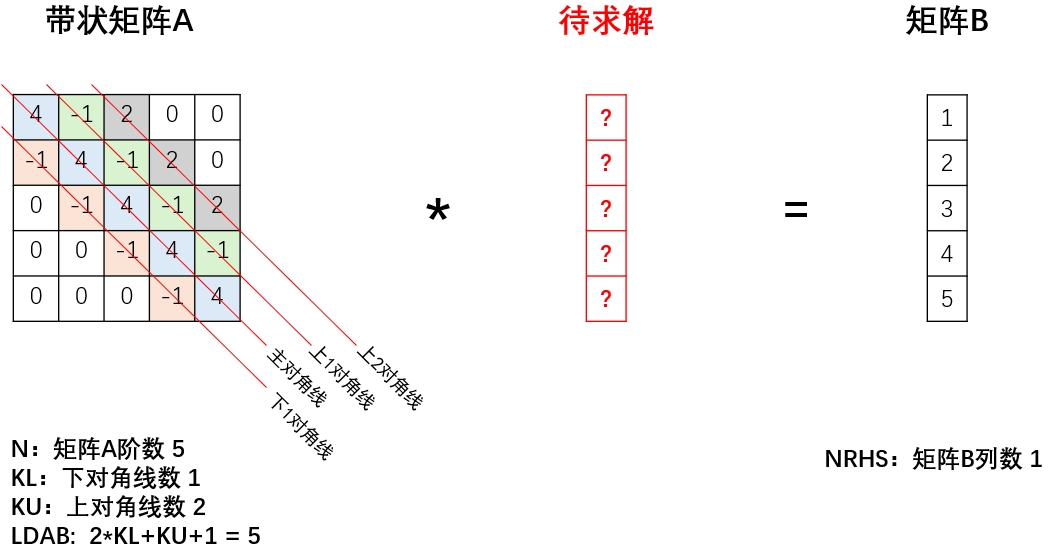
需要对矩阵A进行变换，输入至函数中，变换规则如下：

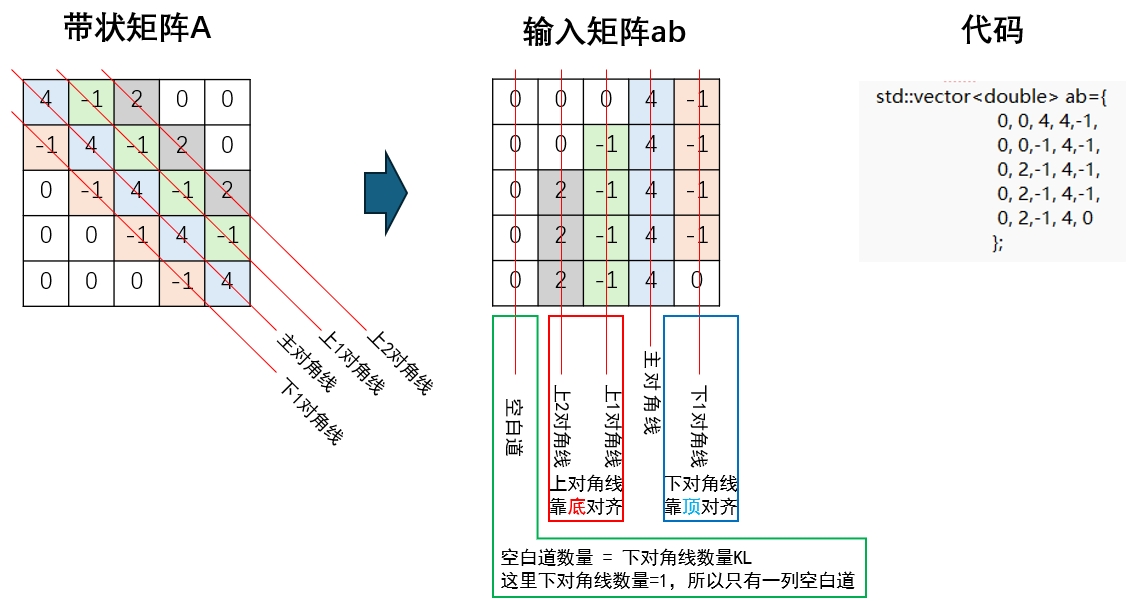
代码及解释如下：

#include <iostream>
#include <vector>
#include <lapacke.h>

Int main(){
    lapack_int n = 5;                 // 矩阵A阶数
    lapack_int kl = 1;                // 下对角线数
    lapack_int ku = 2;                // 上对角线数
    lapack_int ldab = 2*kl + ku + 1;  // 代码所需的参数，直接按公式代入即可
    lapack_int nrhs = 1;              // 矩阵B 列数
    lapack_int ipiv[n];               // 代码所需的固定参数，置换矩阵信息，无需更改

    std::vector<double> ab={ 0, 0, 0, 4,-1,          // 矩阵A的输入格式
                             0, 0,-1, 4,-1,
                             0, 2,-1, 4,-1,
                             0, 2,-1, 4,-1,
                             0, 2,-1, 4, 0 };
    std::vector<double> b={1, 2, 3, 4, 5};           // 矩阵B

    lapack_int info = LAPACKE_dgbsv(LAPACK_COL_MAJOR, n, kl, ku, nrhs, ab.data(), ldab, ipiv, b.data(), n);

    if (info == 0) {
        for (int i = 0; i < n; ++i) {std::cout << "X[" << i << "] = " << b[i] << std::endl;}
    } else if (info > 0) {
        std::cout << "The matrix A is singular. U(" << info << "," << info << ") is exactly zero." << std::endl;
    } else {
        std::cout << "Illegal argument value at position " << -info << std::endl;
    }
    
    return 0;
}