c++输出24点所有情况（1-13）

一、题目描述

随机生成4个代表扑克牌牌面的数字字母，程序自动列出所有可能算出24的表达式，用擅长的语言（C/C++/Java或其他均可）实现程序解决问题。

二、问题分析

使用枚举就能解决问题，难点在于如何减少重复枚举的条件和输出带括号的表达式，这里使用了枚举来输出。

三、算法设计

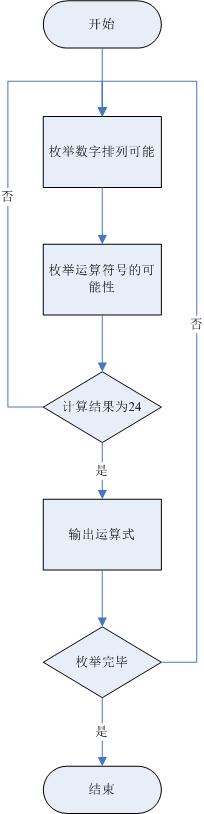
四、代码实现

函数实现

int main()
{
	add();
	system("pause");
}
void add()//依次枚举所有的可能
{
	int a[4];
	for (a[0]=1; a[0] < 14; a[0]++)
		for (a[1]=1; a[1] < 14; a[1]++)
			for (a[2]=1; a[2] < 14; a[2]++)
				for (a[3]=1; a[3] < 14; a[3]++)
				{
					calculate0(a[0],a[1],a[2],a[3]);
				}
}

int calculate0(int q,int w,int e,int r)//将输入的数字进行按所有可能的运算符排列进行计算
{
	int d[4] = { q,w,e,r };
	int a, b, c;
	int i[3] = { 0,0,0 };
	for(;i[0]<6;i[0]++)
		for(; i[1] < 6; i[1]++)
			for (; i[2] < 6; i[2]++)
			{
				switch (i[0])
				{
				case 0:a = d[0] + d[1]; break;
				case 1:a = d[0] - d[1]; break;
				case 2:a = d[0] * d[1]; break;
				case 3:a = d[0] / d[1]; break;
				case 4:a = d[1] - d[0]; break;
				case 5:a = d[1] / d[0]; break;
				default:
					break;
				}
				switch (i[1])
				{
				case 0:b = a + d[2]; break;
				case 1:b = a - d[2]; break;
				case 2:b = a * d[2]; break;
				case 3:b = a / d[2]; break;
				case 4:b = d[2] - a; break;
				case 5:b = d[2] / a; break;
				default:
					break;
				}
				switch (i[2])
				{
				case 0:c = b + d[3]; break;
				case 1:c = b - d[3]; break;
				case 2:c = b * d[3]; break;
				case 3:c = b / d[3]; break;
				case 4:c = d[3] - b; break;
				case 5:c = d[3] / b; break;
				default:
					break;
				}
				if (c == 24)
				{
					cout << d[0] << " " << d[1] << " " << d[2] << " " << d[3] << endl;
					display(d[0], d[1], d[2], d[3], i);
					cout << endl;
				}
			}
	return 0;
}
void display(int q, int w, int e, int r,int* b)//显示计算的结果
{
	int i = 0;
	int a[4] = { q,w,e,r };
	string s,t;
	string c[4];
	for (int i = 0; i < 4; i++)
	{
		if (a[i] < 10)
			c[i] = a[i] + 48;
		else switch (a[i])
		{
		case 10:c[i] = "10"; break;
		case 11:c[i] = "J"; break;
		case 12:c[i] = "Q"; break;
		case 13:c[i] = "K"; break;
		default:
			break;
		}
	}
	switch (b[i++]+1)
	{
	case 1:
		t = "(" + c[i - 1] ;
		s = t + "+" + c[i]+")";
		break;
	case 2:
		t = "(" + c[i - 1];
		s = t + "-" + c[i] + ")";
		break;
	case 3:
		t = "(" + c[i - 1];
		s = t + "*" + c[i] + ")";
		break;
	case 4:
		t = "(" + c[i - 1];
		s = t + "/" + c[i] + ")";
		break;
	case 5:
		t = "(" + c[i];
		s = t + "-" + c[i - 1] + ")";
		break;
	case 6:
		t = "(" + c[i ];
		s = t + "/" + c[i - 1] + ")";
		break;
	default:
		break;
	}
	switch (b[i++] + 1)
	{
	case 1:
		t = "(" ;
		s = t + s + "+" + c[i] + ")";
		break;
	case 2:
		t = "(";
		s = t + s + "-" + c[i] + ")";
		break;
	case 3:
		t = "(";
		s = t + s + "*" + c[i] + ")";
		break;
	case 4:
		t = "(";
		s = t + s + "/" + c[i] + ")";
		break;
	case 5:
		s = "(" + c[i];
		s = t + "-" + s + ")";
		break;
	case 6:
		s = "(" + c[i];
		s = t + "/" + s + ")";
		break;
	default:
		break;
	}
	switch (b[i++] + 1)
	{
	case 1:
		t = "(";
		s = t + s + "+" + c[i] + ")";
		break;
	case 2:
		t = "(";
		s = t + s + "-" + c[i] + ")";
		break;
	case 3:
		t = "(";
		s = t + s + "*" + c[i] + ")";
		break;
	case 4:
		t = "(";
		s = t + s + "/" + c[i] + ")";
		break;
	case 5:
		s = "(" + c[i];
		s = t + "-" + s + ")";
		break;
	case 6:
		s = "(" + c[i];
		s = t + "/" + s + ")";
		break;
	default:
		break;
	}
	cout << s << endl;
}

五、调试和运行结果

调试结果：

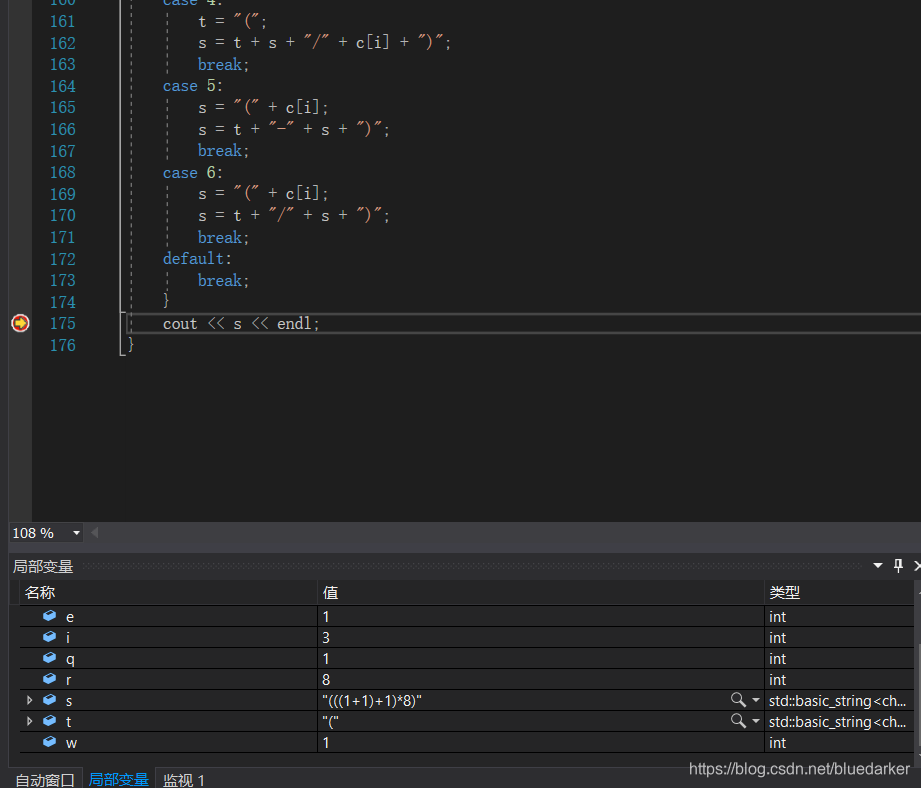
运行结果：

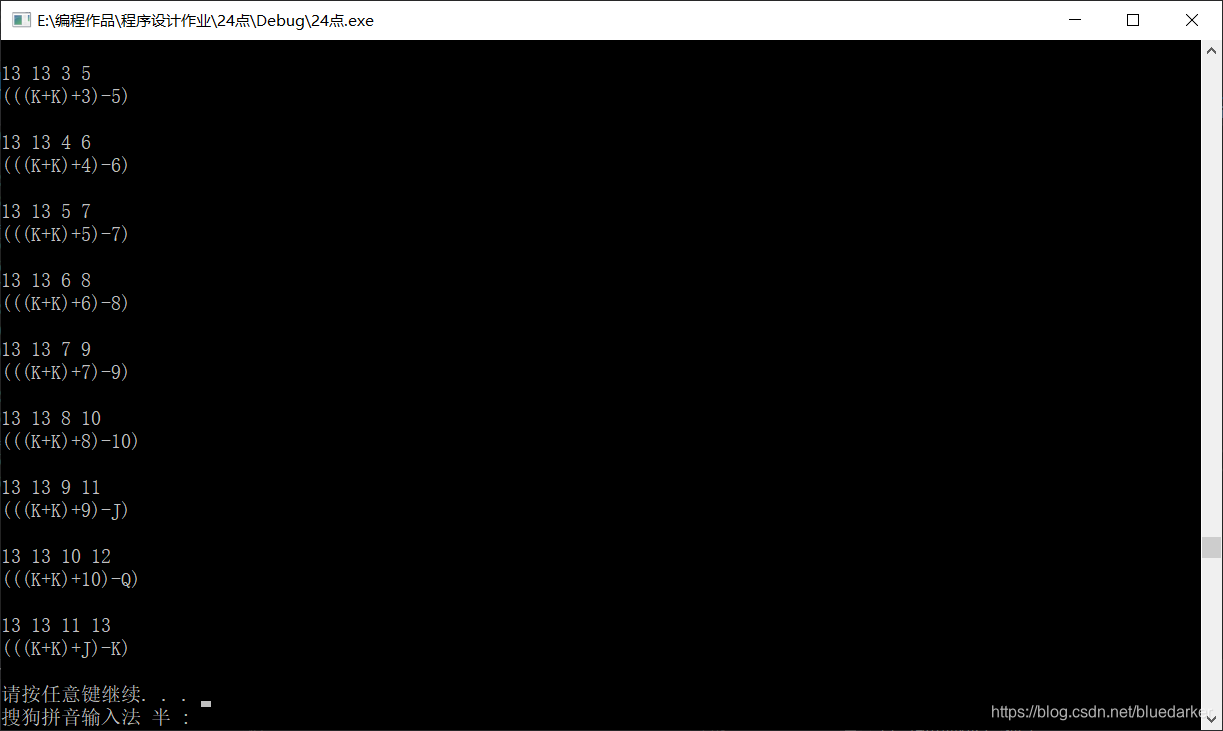
六、心得总结

用相对固定的格式输出运算式，可能存在遗漏，同时采用了对数字组合的全枚举，以及运算符号的特殊性，产生了很多等价的结果。理想情况中使用全排列的方式应该能避免重复，但是个人能力有限，无法实现全排列。