递归作业

一、实验内容

题目1：将非负十进制整数n转换成b进制。（其中b=2~16）
题目2：任何一个正整数都可以用2的幂次方表示。例如：
　　　　137=2⁷⁺²3+2^0　　　　
同时约定幂次方用括号来表示，即ab 可表示为a（b）。
　　 由此可知，137可表示为：
　　　　 2（7）+2（3）+2（0）
进一步：7= 2²⁺²⁺²0 （21用2表示）
　　　　 3=2+2^0
所以最后137可表示为：
　　　　 2（2（2）+2+2（0））+2（2+2（0））+2（0）
　　 又如：
　　　　 1315=2^10 +2^8 +2^5 +2+2^0
所以1315最后可表示为：
　　 2（2（2+2（0））+2）+2（2（2+2（0）））+2（2（2）+2（0））+2+2（0）
　　输入：正整数（n≤20000）
输出：符合约定的n的0，2表示（在表示中不能有空格）
输入格式 Input Format
一个正整数
输出格式 Output Format
符合约定的n的0，2表示（在表示中不能有空格）
样例输入 Sample Input
73
样例输出 Sample Output
2(2(2)+2)+2(2+2(0))+2(0)

二、问题分析

两个问题可以使用字符串拼接来实现，问题1通过不断取余然后往字符串前面加数字。问题二现将数字表示为2（n）+…+2（0），对指数进行递归。

三、算法设计

问题1递归模型：

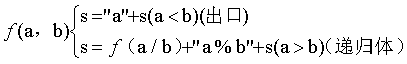
问题2递归模型：

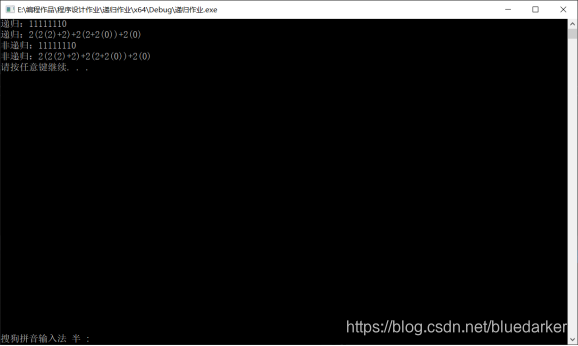
四、运行结果与部分调试截图

运行截图

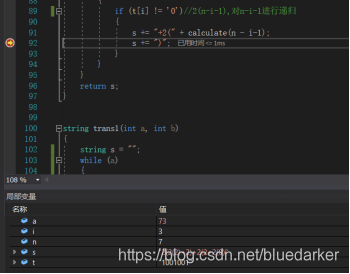
调试截图

五、总结

问题主要出现在问题2，对其中的函数出口控制最开始有问题，本来2理应直接用2表示的，但是我程序的最开始的结果却是2（2（0）），后来通过增加出口并且直接将递归体后两位直接不使用递归的方法解决问题。其非递归主要使用枚举，本来是想用类似于递归的方法求解，但是出现错误，于是直接采用枚举，以达到简单解决问题的目的。