理解和获取应用领域中的数据需求，描述数据范围、属性特征、数据关系，支持用户数据处理需求

以下是关于数据库设计、UML建模、C/C++/Java算法实现（以分治法、动态规划法为例）的相关脑图内容：

数据库设计脑图

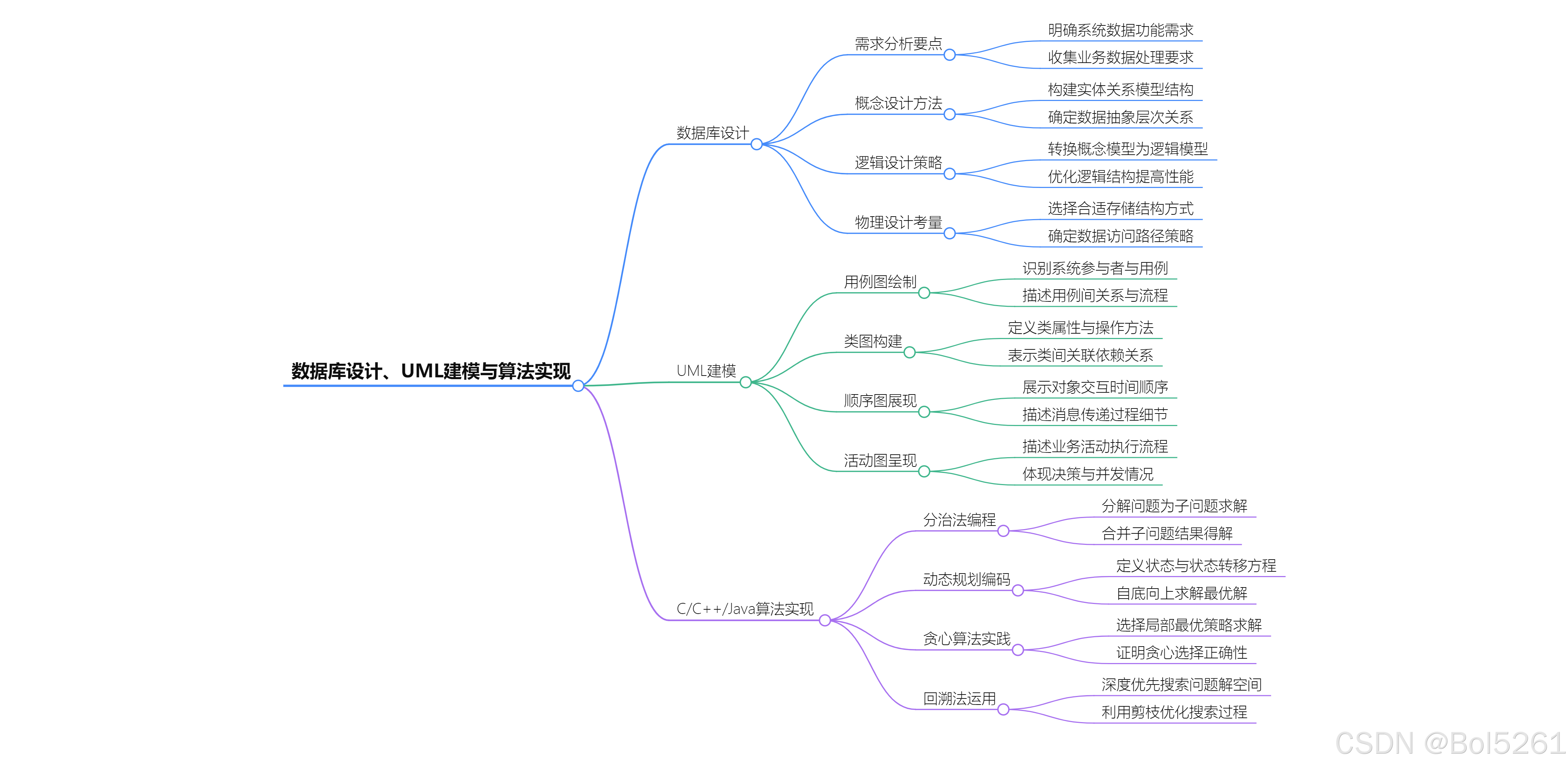
• 需求分析：理解和获取应用领域中的数据需求，描述数据范围、属性特征、数据关系，支持用户数据处理需求。
• 概念设计：通过数据抽象，设计局部概念模型，再综合为全局概念模型，常用ER模型，产生反映用户单位信息需求的数据库概念结构。
• 逻辑设计：把概念模型转化为DBMS能处理的逻辑模型，设计外模型、应用程序与数据库的接口，评价和修正模型。
• 物理设计：选取适合应用环境的物理结构，考虑数据存储方案，如文件组织方式、索引技术等，以加快数据检索速度。
• 实现：根据设计好的逻辑和物理结构，在数据库管理系统中创建数据库、表等对象，插入数据等。
• 运行维护：对数据库进行监控、性能优化、备份恢复、安全性管理等，确保数据库正常运行。

UML建模脑图

• 概述：统一建模语言，用于设计软件蓝图的可视化建模语言，支持面向对象系统的分析、设计、实现和交付等环节。
• 构造块：
  • 事物：对模型中最具代表性的成分的抽象。
  • 关系：把事物结合在一起，如关联、聚合、组合、继承等关系。
  • 图：聚集了相关的事物。
• 图的类型：
  • 结构图：如类图，描述系统的类、属性、方法及类之间的关系；对象图是类图的实例；构件图描述代码构建的物理结构及依赖关系等。
  • 行为图：如用例图描述角色与用例之间的关系；活动图描述活动及活动间约束关系；状态图描述对象状态及状态转移条件；序列图显示参与者与系统对象交互的顺序步骤等。

C/C++/Java算法实现脑图

• 分治法：
  • 原理：将规模为n的问题分为k个规模较小、相互独立且与原问题相同的子问题，递归地解决子问题，再将子问题的解合并为原问题的解。
  • 经典算法：二分搜索、合并排序、快速排序、Strassen矩阵乘法、最接近点对问题、大整数乘法、棋盘覆盖、比赛日程表安排等。
• 动态规划法：
  • 原理：将一个复杂问题分解为若干个重叠的子问题，通过求解子问题并保存其解，避免重复计算，从而高效地解决原问题。
  • 关键要素：最优子结构（问题的最优解包含子问题的最优解）、子问题重叠性质。
  • 应用场景：背包问题、最长公共子序列、矩阵链乘法、最短路径问题等。

你可以根据以上内容，使用专业的脑图软件（如Xmind、MindManager等）或在线脑图工具（如ProcessOn等）来绘制具体的脑图，以便更直观地展示和理解相关知识体系。

以下是以 数据库设计、UML建模、C/C++/Java算法实现（分治法/动态规划） 为核心的 脑图结构（文字版），可直接复制到XMind/MindMaster等工具中生成可视化脑图：

---

📊 数据库设计

• 需求分析
  • 业务场景梳理（用户/订单/库存等）
  • 功能需求（增删改查/报表/事务）
• 概念设计（E-R模型）
  • 实体（用户、商品、订单）
  • 关系（1:N、M:N、弱实体）
  • 属性（主键/外键/复合属性）
• 逻辑设计（关系模式）
  • 范式（1NF/2NF/3NF/BCNF）
  • 反范式（冗余优化）
  • 约束（主键/外键/检查约束）
• 物理设计
  • 索引（B+树/哈希/位图）
  • 分区（水平/垂直/分库分表）
  • 引擎选择（InnoDB/MyISAM）
• 优化与安全
  • SQL调优（EXPLAIN/慢查询）
  • 权限（RBAC模型）
  • 备份（主从复制/日志）

---

🏗️ UML建模

• 结构图
  • 类图（属性/方法/关联/继承/接口）
  • 对象图（实例快照）
  • 组件图（模块依赖）
  • 部署图（硬件节点）
• 行为图
  • 用例图（参与者/系统边界）
  • 时序图（对象交互/生命线）
  • 活动图（流程分支/并发）
  • 状态机图（状态转换事件）
• 设计模式
  • 创建型（单例/工厂/建造者）
  • 结构型（适配器/装饰器/代理）
  • 行为型（观察者/策略/模板方法）

---

💻 算法实现

分治法（Divide & Conquer）

• 核心思想
  • 分解 → 解决 → 合并
• 经典案例
  • 快速排序（C/Java）
  • 归并排序（C++）
  • 最近点对问题（二维分治）
• 复杂度分析
  • T(n)=aT(n/b)+f(n) → 主定理

动态规划（Dynamic Programming）

• 核心思想
  • 最优子结构 + 重叠子问题
• 实现方式
  • 记忆化递归（Top-down）
  • 递推表（Bottom-up）
• 经典案例
  • 背包问题（0-1/完全/多重）
  • 最长公共子序列（LCS）
  • 最短路径（Floyd-Warshall）
• 代码模板（Java示例）

  int[] dp = new int[n+1];
  for (int i=1; i<=n; i++) {
      dp[i] = Math.max(dp[i-1], dp[i-2]+val[i]);
  }
  

---

🔗 工具与扩展

• 数据库：MySQL Workbench、PowerDesigner
• UML：StarUML、PlantUML、Visual Paradigm
• 算法调试：CLion（C++）、IntelliJ（Java）、GDB

---

使用建议

1. 数据库设计 先画E-R图 → 再转关系模式 → 最后物理优化。
2. UML建模 从用例图→类图→时序图逐层细化。
3. 算法实现 先画递归树/状态转移表 → 再编码（优先Java/Python验证逻辑）。