通过以上特征可以看出，动态规划法的本质是**利用“重叠子问题”和“最优子结构”，通过存储子问题结果来减少计算量，从而高效求解复杂问题*-优快云博客

本文链接：https://blog.youkuaiyun.com/blog_programb/article/details/149550102

下面我将展示使用动态规划法解决斐波那契数列问题的两种常见实现方式：自顶向下的记忆化方法和自底向上的表格法。

斐波那契数列的定义是：F(0) = 0，F(1) = 1，F(n) = F(n-1) + F(n-2)（n ≥ 2）

# 方法1：自顶向下（记忆化递归）
def fib_memoization(n, memo=None):
    # 初始化记忆字典
    if memo is None:
        memo = {0: 0, 1: 1}
    
    # 如果已计算过，直接返回记忆中的结果
    if n in memo:
        return memo[n]
    
    # 否则计算并存储结果
    memo[n] = fib_memoization(n-1, memo) + fib_memoization(n-2, memo)
    return memo[n]


# 方法2：自底向上（表格法）
def fib_tabulation(n):
    # 处理基础情况
    if n == 0:
        return 0
    if n == 1:
        return 1
    
    # 创建表格存储子问题结果
    dp = [0] * (n + 1)
    dp[0] = 0
    dp[1] = 1
    
    # 从最小子问题开始计算，逐步构建到目标问题
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    
    return dp[n]


# 测试代码
if __name__ == "__main__":
    n = 10
    print(f"斐波那契数列第 {n} 项（记忆化方法）：{fib_memoization(n)}")
    print(f"斐波那契数列第 {n} 项（表格法）：{fib_tabulation(n)}")
    
    # 输出前10项验证
    print("\n斐波那契数列前10项：")
    for i in range(10):
        print(fib_tabulation(i), end=" ")

代码解析：

自顶向下（记忆化递归）：
- 使用字典memo存储已计算的子问题结果
- 递归过程中先检查是否已计算，避免重复计算
- 时间复杂度：O(n)，空间复杂度：O(n)（递归栈+记忆字典）
自底向上（表格法）：
- 使用数组dp作为表格存储子问题结果
- 从最小的子问题（F(0)、F(1)）开始计算，逐步推导出更大的问题
- 时间复杂度：O(n)，空间复杂度：O(n)（可优化至O(1)，因为只需要前两项）

两种方法都利用了动态规划的核心思想：存储子问题的解以避免重复计算，相比朴素递归的O(2ⁿ)时间复杂度有了极大提升。在实际应用中，表格法通常效率更高，因为避免了递归调用的开销。

动态规划擅长处理满足以下三类特征的子问题：

重叠子问题（Overlapping Sub-problems）
子问题空间中存在大量重复计算；同一子问题会被不同父问题多次调用。
最优子结构（Optimal Sub-structure）
原问题的最优解可由若干子问题的最优解组合而成，且子问题之间相互独立。
无后效性（No After-effect）
子问题的解一旦确定，不再受后续决策的影响；状态转移只依赖于之前的状态，而不依赖于到达该状态的路径。

典型例子

序列型：最长公共子序列（LCS）、编辑距离、最长递增子序列（LIS）
区间型：矩阵链乘法、石子合并、回文子串
背包型：0/1 背包、完全背包、多重背包
树形/图型：树上的最大独立集、最短路径（Floyd–Warshall）
博弈型：取石子游戏、数字三角形
数位型：数位 DP（统计满足某种条件的数字个数）

只要子问题同时满足“重叠、最优子结构、无后效”三要素，就可用动态规划统一处理。

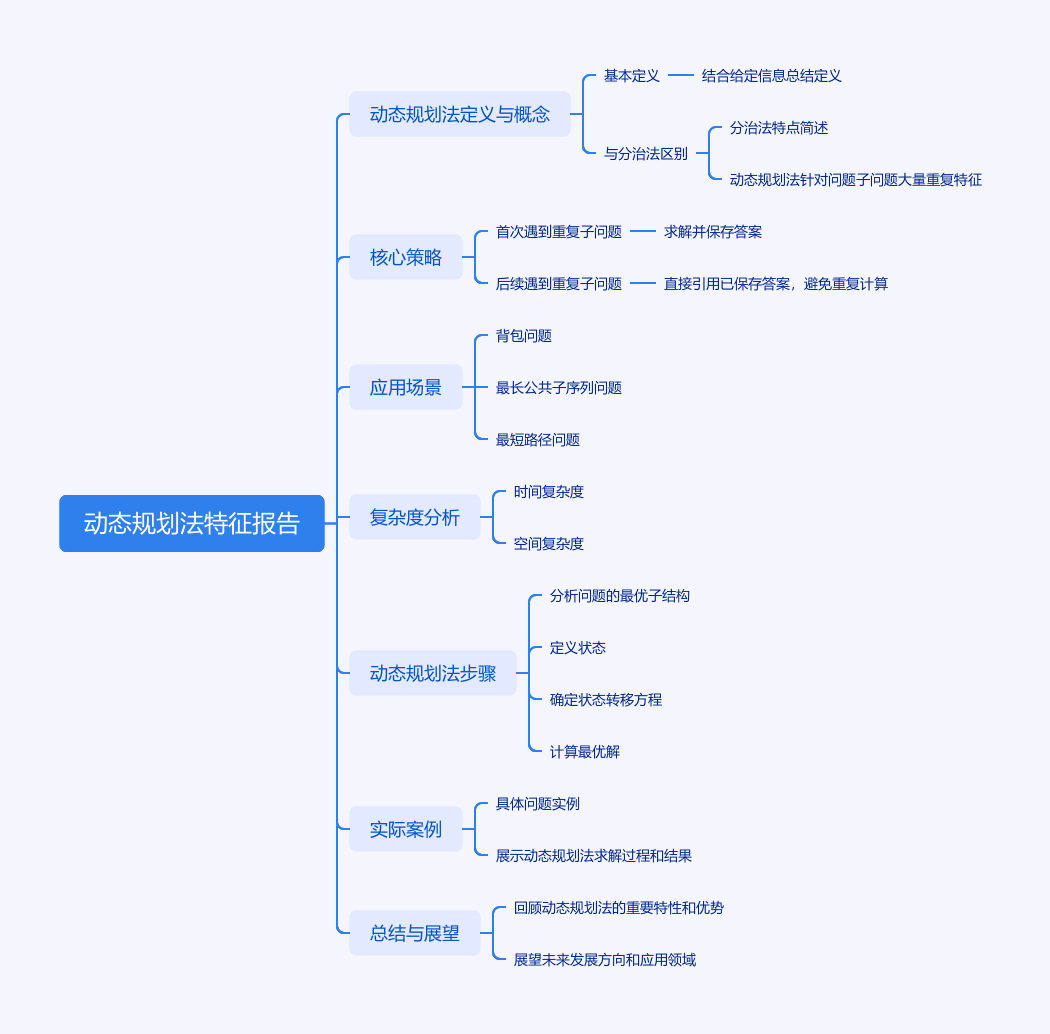
动态规划法（Dynamic Programming, DP）的核心特征总结

问题具备重叠子问题（Overlapping Subproblems）
- 问题可以分解为多个子问题，且这些子问题在求解过程中会被重复多次（与分治法的“子问题独立不重复”形成核心区别）。
- 例如：斐波那契数列中，计算 fib(5) 需要 fib(4) 和 fib(3)，而计算 fib(4) 又需要 fib(3) 和 fib(2)，其中 fib(3) 就是重复出现的子问题。
问题具备最优子结构（Optimal Substructure）
- 问题的最优解可以由其子问题的最优解推导而来。即，通过求解子问题的最优解，能够组合出原问题的最优解。
- 例如：最短路径问题中，从A到C的最短路径若经过B，则A到B的路径和B到C的路径也必须是各自的最短路径。
核心策略：记忆化（Memoization）或表格法（Tabulation）
- 记忆化（自顶向下）：递归求解过程中，首次遇到子问题时计算结果并存储（如用哈希表或数组），后续直接调用存储的结果，避免重复计算。
- 表格法（自底向上）：先求解最小规模的子问题，将结果存储在表格（数组）中，再基于子问题的结果逐步求解更大规模的问题，最终得到原问题的解（无递归，效率更高）。
通过状态转移方程定义问题
- 用数学公式描述原问题与子问题的关系，即“状态转移方程”。例如：斐波那契数列的状态转移方程为 dp[n] = dp[n-1] + dp[n-2]（其中 dp[n] 表示第n项的值）。

与分治法的核心区别对比

特征	动态规划法	分治法
子问题特性	子问题重叠重复	子问题独立不重复
核心策略	存储子问题结果，避免重复计算	递归分解后独立求解子问题，不存储结果
适用场景	优化问题（如最短路径、最大价值）或有重复子问题的问题	分治问题（如归并排序、快速排序、二分查找）

通过以上特征可以看出，动态规划法的本质是利用“重叠子问题”和“最优子结构”，通过存储子问题结果来减少计算量，从而高效求解复杂问题。其核心思想是“以空间换时间”，适用于大量重复子问题的场景。

返回图片