**把问题的所有可能解抽象成一棵树（或图），然后用深度优先搜索（DFS）去遍历这棵树，一边走一边判断当前路径是否满足条件，满足就继续深入，不满足就“回头”换路，直到找出所有可行解或最优解

回溯法的核心思路可以概括为一句话：

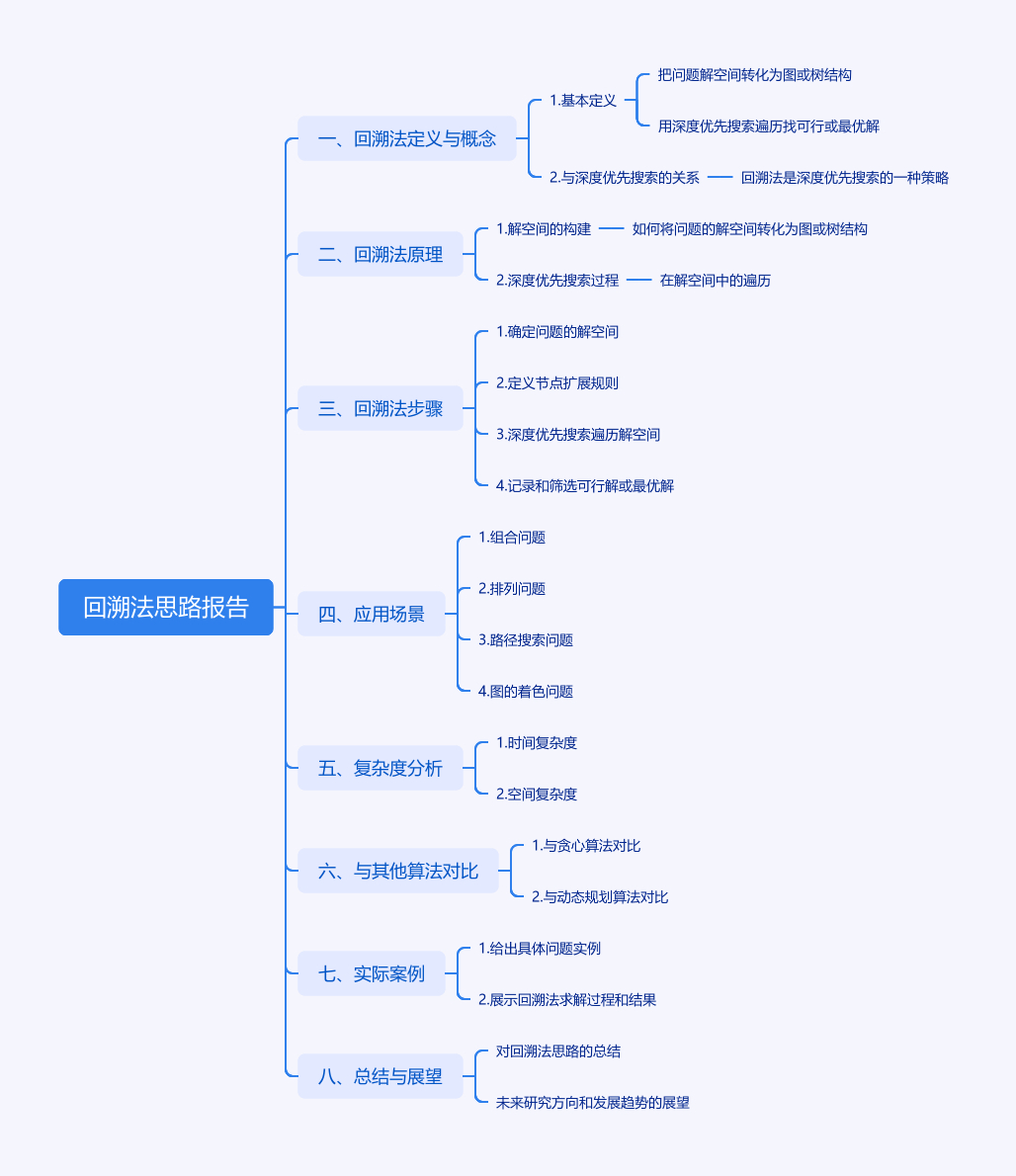
把问题的所有可能解抽象成一棵树（或图），然后用深度优先搜索（DFS）去遍历这棵树，一边走一边判断当前路径是否满足条件，满足就继续深入，不满足就“回头”换路，直到找出所有可行解或最优解。

简单理解就是：“走到底，走不通就退回，换个方向再走。”

你对回溯法思路的描述很准确！回溯法（Backtracking）是一种通过试错来寻找问题解的算法，其核心逻辑可以进一步拆解为以下几个关键步骤，帮助更直观地理解：

1. 定义解空间（解的可能范围）

• 将问题的所有可能解抽象为一个树状结构（称为“解空间树”），树的每个节点代表一个部分解，每条路径代表从初始状态到某个部分解的过程。
• 例如：“n皇后问题”中，解空间树的第i层节点表示第i行皇后的摆放位置，路径则对应前i行皇后的具体位置组合。

2. 深度优先搜索（DFS）遍历解空间

• 从根节点出发，按照深度优先的顺序探索子节点（即逐步构建解的每一部分）。
• 每一步选择一个可能的选项，继续向下探索，直到无法再深入（到达叶子节点）或发现当前路径不可能得到有效解。

3. 剪枝（Pruning）：排除无效路径

• 在遍历过程中，若发现当前部分解已违反问题的约束条件（如n皇后问题中出现同列或同斜线冲突），则立即停止该路径的探索，回溯到上一层节点，尝试其他可能的选项。
• 剪枝是回溯法提高效率的关键，避免了对无效解的完整搜索。

4. 记录有效解

• 当遍历到叶子节点时，若当前路径对应的解满足所有约束条件，则记录该解（若问题要求最优解，还需比较并保留最优结果）。

简单类比

可以把回溯法想象成“走迷宫”：

• 迷宫的每个岔路口是解空间树的节点，每条岔路是一个可能的选择；
• 沿着一条路走到死胡同（违反约束），就退回到上一个岔路口换条路走（回溯）；
• 直到找到出口（有效解），或尝试所有路径后确认无解。

回溯法适用于解决组合优化、排列、子集等问题（如八皇后、数独、0-1背包等），其时间复杂度通常较高，但通过剪枝可以显著优化实际运行效率。

在回溯法中，DFS（深度优先搜索）的作用可以概括为一句话：
“系统地、一条道走到头地生成并验证候选解，一旦发现走不通立即回溯，从而避免无效搜索。”

具体分解：

1. 生成解路径
   DFS 沿着解空间树的一条分支一直深入，逐层为解的每个分量做选择（如八皇后逐行放皇后、子集问题逐元素选/不选），从而“搭”出一条完整的候选解。

2. 剪枝与回溯
   在深入过程中，一旦发现当前部分解已违反约束（如冲突、越界、超界），DFS 立即返回上一层（回溯），不再继续搜索以该节点为根的子树，实现“剪枝”。

3. 记录可行解/最优解
   当 DFS 走到叶子节点且满足所有约束时，记录当前完整解；若要求最优解，则在记录的同时更新全局最优值。

4. 撤销选择（状态恢复）
   回溯返回上一层前，必须撤销当前层对全局状态所做的修改（如棋盘复位、计数器减一），保证上一层循环的下一轮选择是在“干净”的状态下进行。

总结：DFS 是回溯法用来“逐层构造、即时验证、遇错回退、穷举所有可能”的遍历引擎。