图像生成模型

目录

1. GAN

目标：

数学目标：

推导过程：

目标函数：

2. VAE

目标：

数学目标：

 推导过程：

目标函数：

Diffusion

目标：

数学目标：

 推导过程：

目标函数:

---

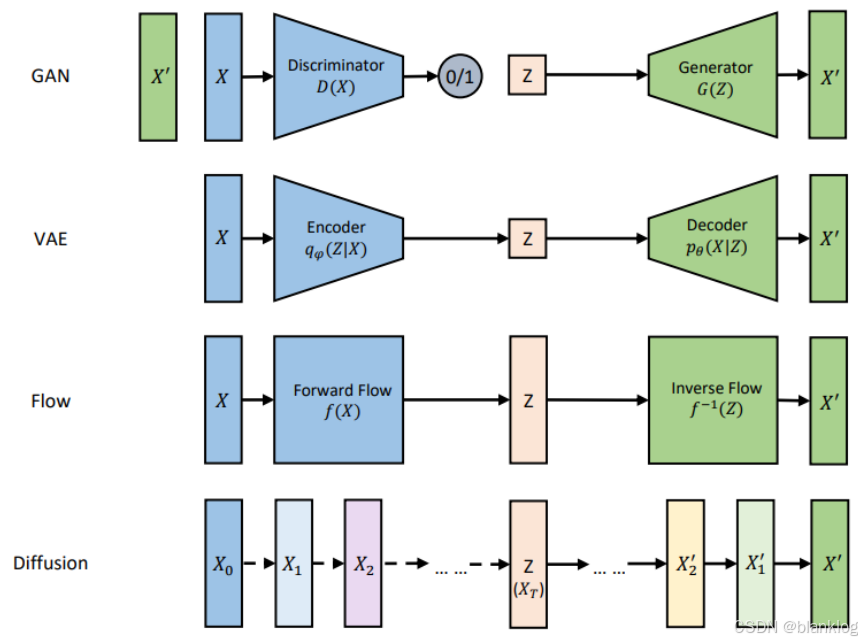
1. GAN

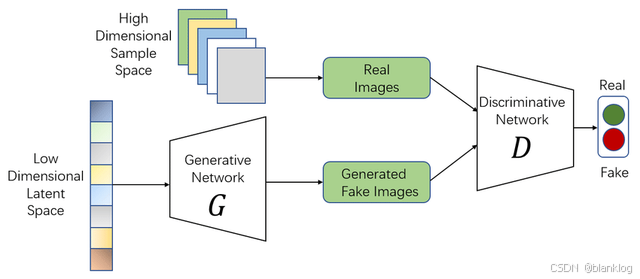
目标：

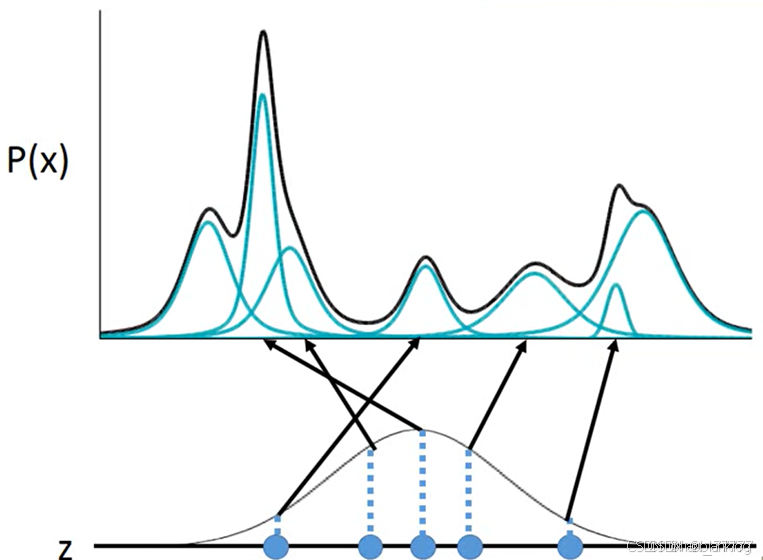
训练一个生成器去拟合真实样本的分布 ，然后通过生成器从这个分布中进行采样。

数学目标：

为最小化样本和生成器分布的KL散度：

推导过程：

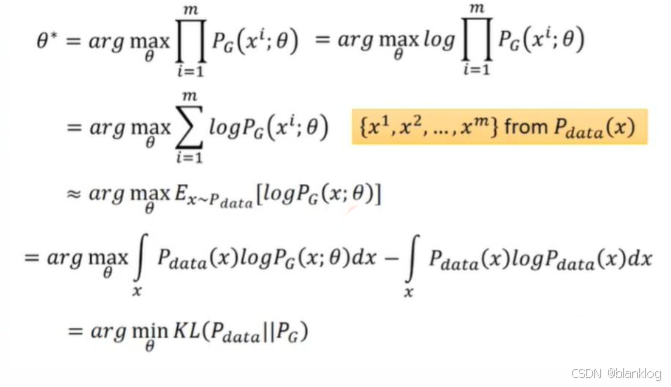
目标函数：

当判别器太强或样本分布太复杂，生成器会偷懒产生模式坍塌。 

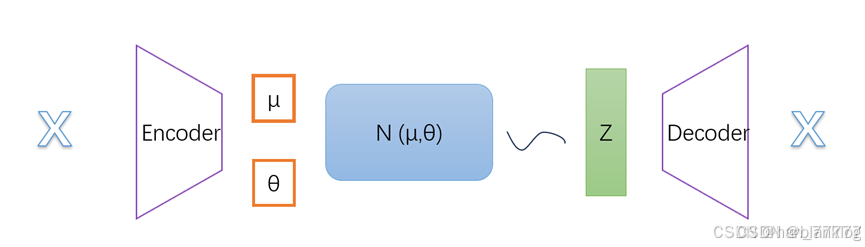
2. VAE

目标：

训练一个生成器去拟合真实样本的分布 ，然后通过生成器从这个分布中进行采样；

添加了一个约束假设，既p(z|x)服从N(0,1)分布。

数学目标：

为最大化证据下界。

 推导过程：

目标函数：

 

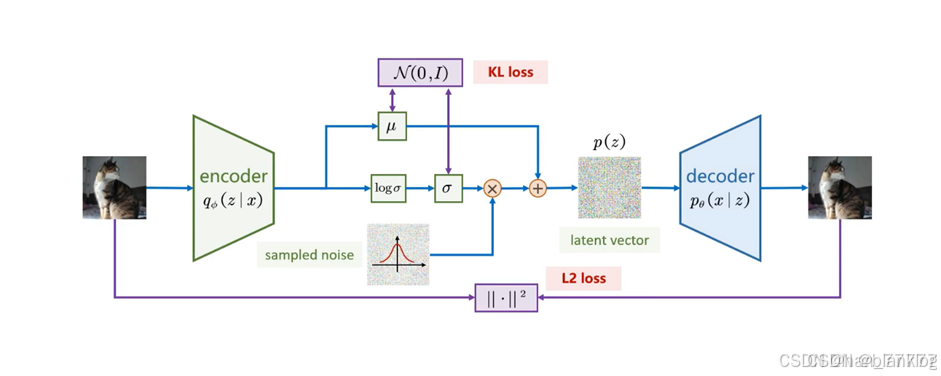
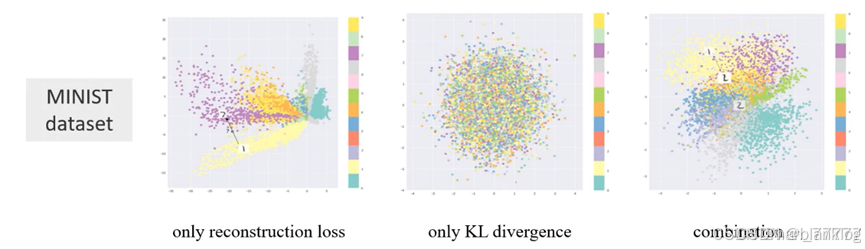
Diffusion

目标：

训练一个生成器去拟合真实样本的分布 ；从t时刻的扩散噪声中一步步恢复出真实数据分布，模型预测t时刻的噪声，用来采样t-1时刻的图像。

假设：前向扩散过程噪声服从N~(0,1)分布。

推导：逆向过程服从高斯分布，均值和方差跟,x0,xt和扩散参数有关。

数学目标：

VAE: 

Diffusion:

 推导过程：

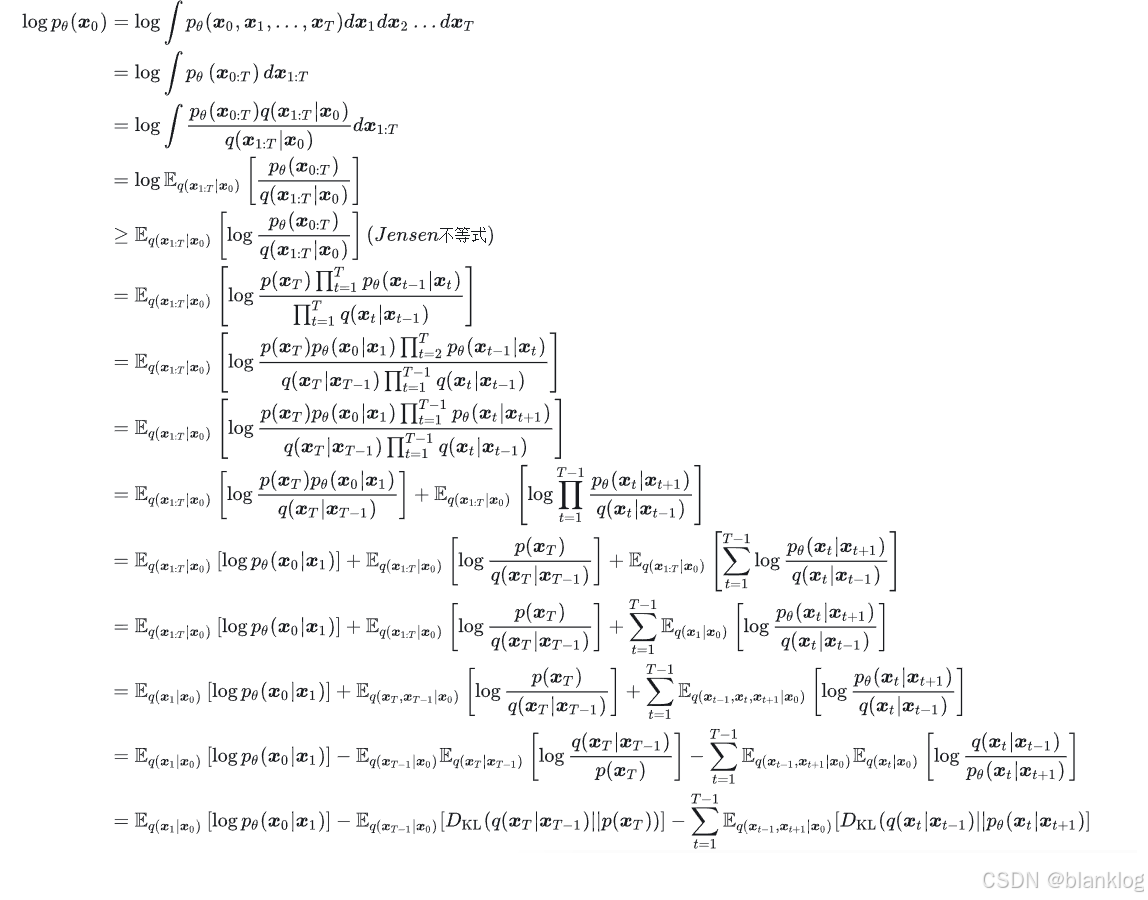
简化：

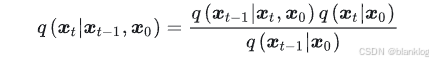
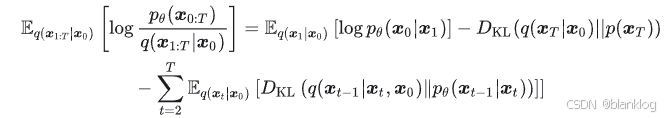
第二项无参数，只优化第一项和第三项即可，第一项可看作第三项T=1的情况。

目标函数:

根据 t 时刻的图像预测其t时刻的噪声，使得 的分布与真实的分布相近。