MultiCol-Slam里面的cayley变换/参数

cayley变换/参数

参考链接：

1. http://blog.leanote.com/post/610167078@qq.com/cayley%E5%8F%98%E6%8D%A2
2. https://blog.youkuaiyun.com/J10527/article/details/70140264

旋转向量与旋转矩阵之间的相互转换是通过罗德里格斯公式建立起来的：

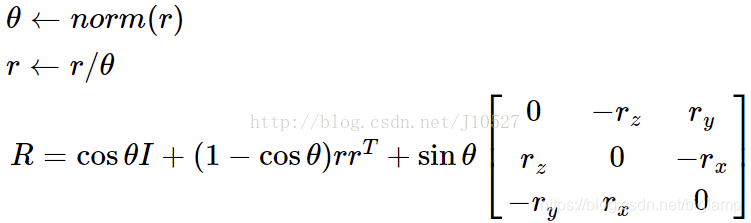
其中r为旋转向量，R为旋转矩阵。其反过程可有下式确定：

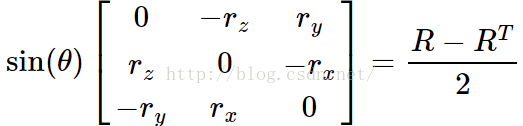
除此之外，还有凯莱公式（Cayley formula）可以将旋转向量转化为旋转矩阵，该公式也有说是欧拉发现的：

 

其中A为旋转向量对应的反对称阵。值得一提的是，同一个旋转向量用凯莱公式和罗德里格斯公式转化得到的旋转矩阵通常并不相等，但都是旋转矩阵。

凯莱公式的逆变换为：

<