郑州四中国庆模拟赛其中一场

最新推荐文章于 2025-12-18 16:28:22 发布

原创最新推荐文章于 2025-12-18 16:28:22 发布 · 731 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #图论

前言

~~看到自己高中学校的oj比自己学校的oj还豪华瞬间绷不住了~~
起因是，高中同学wqc在群里招募，然后我就去试试水了_{结果被吊打}
貌似同届的只有我一个人在认真打。
赛时就写了A题正解，B题把公式全忘了不会做，C糊了个自己都觉得假完了的贪心（但是意外过了所有的大小样例？），D写了模拟暴力。
然后看高中那群人，top1差点AK，我第一题还因为开小数组范围挂了，反正自己菜飞了
在这里插入图片描述

题解

A

在这里插入图片描述

思路

一道图论水题，第一眼还以为是我之前写的割点题，结果只是一道并查集存连通块的题目。
了解题意后，我们发现正做此题没什么意思，不妨倒着求解。题目就变成，假设全部点都消失，按顺序加点，判断所有连通块最大权值。
用并查集维护即可

代码实现

#include <bits/stdc++.h>
#define int long long
#define N 500005//考试开成1e5了
#define M 500005
#define debug(x) cout<<#x<<":"<<x<<" ";

using namespace std;
//using namespace __gnu_pbds;
int T,n,m;
struct edge
{
	int next;
	int u,v;
}e[M];
int head[N],cnt;
int a[N],ans[N],sum[N],maxn=0,qu[N];
int fa[N];

int yfind(int u1)
{
	if(fa[u1]==u1) return u1;
	return fa[u1]=yfind(fa[u1]);
}
void yadd(int u,int v)
{
	++cnt;
	e[cnt].u=u;
	e[cnt].v=v;
	e[cnt].next=head[u];
	head[u]=cnt;
}
bool valid[N];
signed main()
{
//	freopen("qd.in","r",stdin);
//	freopen("qd.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	for(int t=1;t<=n;++t)
	{
		scanf("%lld",&a[t]);
		fa[t]=t;
	}
	for(int t=1;t<=m;++t)
	{
		int u1,u2;
		scanf("%lld%lld",&u1,&u2);
		yadd(u1,u2);
		yadd(u2,u1);
	}
	for(int t=1,u1;t<=n;++t)
	{
		scanf("%lld",&qu[t]);
	}
	for(int t=n;t>=2;--t)
	{
		int p=qu[t];
		valid[p]=1;
		sum[p]=a[p];
		for(int i=head[p];i;i=e[i].next)
		{
			int to=e[i].v;
			if(!valid[to]) continue;
			if(yfind(to)!=p)
			{
				sum[p]+=sum[yfind(to)];
				fa[yfind(to)]=p;
			}
		}
		maxn=max(maxn,sum[p]);
		ans[t]=maxn;
	}
	ans[n+1]=0;
	for(int t=2;t<=n+1;++t) printf("%lld\n",ans[t]);
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}

B

思路

首先观察 $f (n, k)$
$k = 1$ 时， $f(n,1)=∑x1=0n(nx1)=∑x1=0n(nx1)∗1x1∗1n−x1=(1+1)n=2nf(n,1)=\displaystyle\sum\limits_{x_1=0}^n\binom{n}{x_1}=\sum\limits_{x_1=0}^n\binom{n}{x_1}*1^{x_1}*1^{n-{x_1}}=(1+1)^{n}=2^n$

$k = 2$ 时， $f(n,2)=∑x1=0n(nx1)∗∑x2=0x1(x1x2)f(n,2)=\displaystyle\sum\limits_{x_1=0}^n\binom{n}{x_1}*\sum\limits_{x_2=0}^{x_1}\binom{x_1}{x_2}$

先对内函数化简得到 $∑x2=0x1(x1x2)=2x1\displaystyle\sum\limits_{x_2=0}^{x_1}\binom{x_1}{x_2}=2^{x_1}$

代入得 $f(n,2)=∑x1=0n(nx1)∗2x1=∑x1=0n(nx1)∗2x1∗1n−x1=3nf(n,2)=\displaystyle\sum\limits_{x_1=0}^n\binom{n}{x_1}*2^{x_1}=\sum\limits_{x_1=0}^n\binom{n}{x_1}*2^{x_1}*1^{n-x_1}=3^n$

大胆假设 $f(n,k)=(k+1)^n$
接下来用归纳法证明：

首先当 $k = 0 (或 1)$ ， $f (n, 0) = 1$ 成立
假设 $f(n,k)=(k+1)^n$ 成立
接下来如果 $f(n,k+1)=(k+2)^n$ 成立，我们假设的结论就成立。
$f(n,k+1)=∑x1=0n(nx1)∗f(x1,k)=∑x1=0n(nx1)∗(k+1)x1=((k+1)+1)n=(k+2)nf(n,k+1)=\displaystyle\sum\limits_{x_1=0}^n\binom{n}{x_1}*f(x_1,k)=\displaystyle\sum\limits_{x_1=0}^n\binom{n}{x_1}*(k+1)^{x_1}=((k+1)+1)^n=(k+2)^n$
所以结论成立。
所以我们需要求解的答案可以转化为
$998244853ans=\sum\limits_{i=0}^{n}(i+1)^{(i+1)^n}\bmod 998244853$
需要注意的是
由于指数非常的大，如果不取模，远远超出快速幂承受的范围，所以我们需要结合费马小定理进行降幂
直接说结论，由于底数模是一个大质数，所以指数模一定是它的欧拉函数，即
$ϕ(998244853)=998244853−1\phi(998244853)=998244853-1$
至于为什么是这个，我会在之后数论笔记里补充。
容易犯得错误是，把底数模当成指数模
$pa^e \bmod p\not\equiv a^{e\bmod p}\bmod p$

代码实现

#include <bits/stdc++.h>
#define int long long
#define N
#define debug(x) cout<<#x<<":"<<x<<" ";

using namespace std;
//using namespace __gnu_pbds;
int T,n,m,k,modd=998244853;
int power(int u1,int u2,int u3)
{
	int sum=1;
	while(u2)
	{
		if(u2&1)
		{
			sum*=u1;
			sum%=u3;
		}
		u1=u1*u1;
		u1%=u3;
		u2>>=1;
		u1%=u3;
	}	
	return sum;
}

signed main()
{
//	freopen("fcf.in","r",stdin);
//	freopen("fcf.out","w",stdout);
	cin>>T;
	while(T--)
	{
		scanf("%d",&n);
		int ans,Ans=0;
		for(int t=0;t<=n;++t)
		{
			ans=power(t+1,n,modd-1);
			Ans+=power(t+1,ans,modd);
		}
		printf("%lld\n",Ans%modd);
	}
	
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}

C

在这里插入图片描述

思路

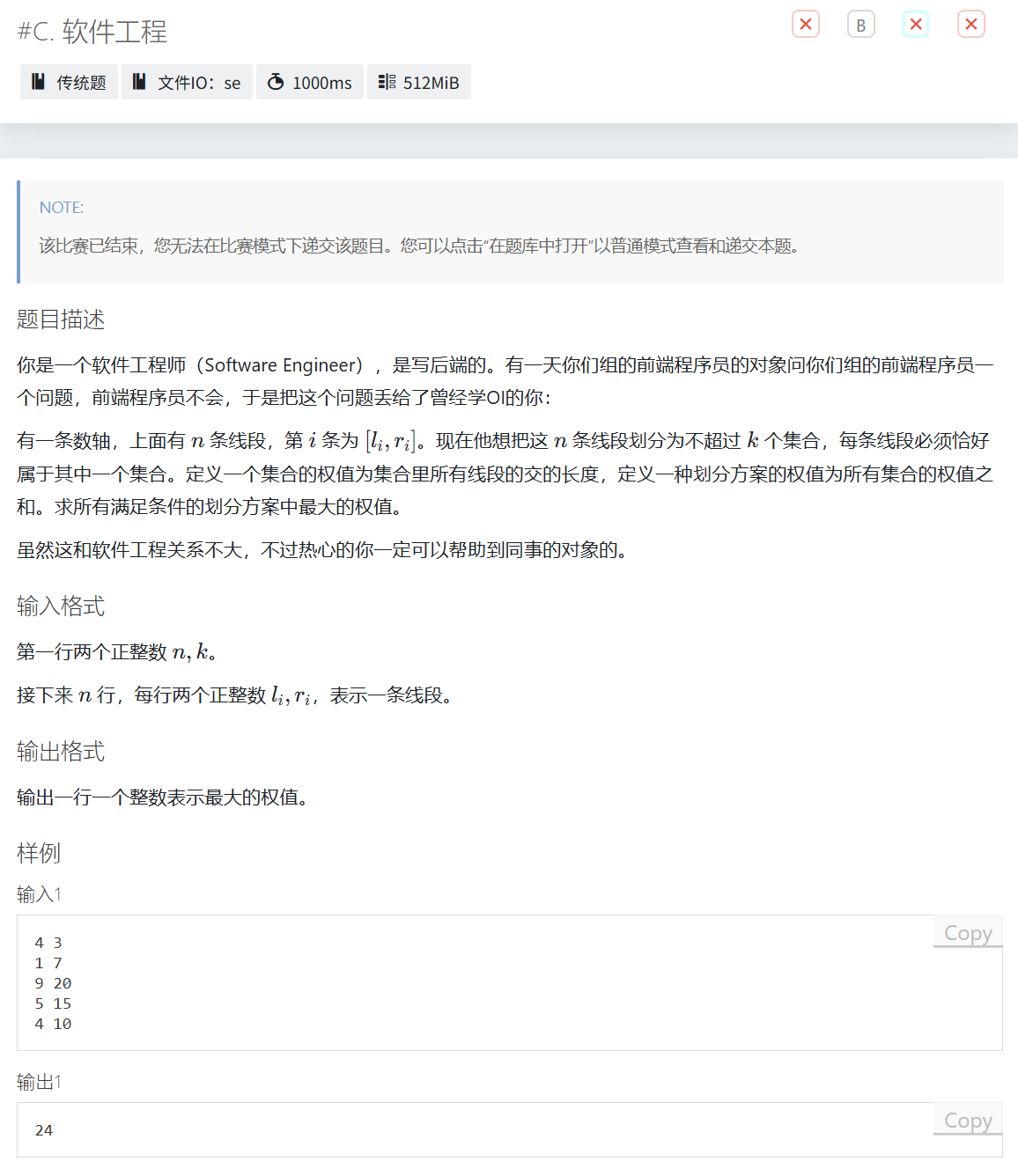
这一题大概率是一道贪心题，但我的贪心写假了。这里只提供一点点思路，并没有正解。
首先，如果没有k的限制，最好的情况就是把每一个线段都单独分到一个集合。
加上了k的限制，先按照线段长度从大到小排序，把前k大的线段都单独分到一个集合里，再依次把剩余没分的线段分配进去。
我写的贪心策略是分配的时候按照对当前答案影响最小的来分。
显然是错误的，评测结果是30%AC，就不贴代码了。

D

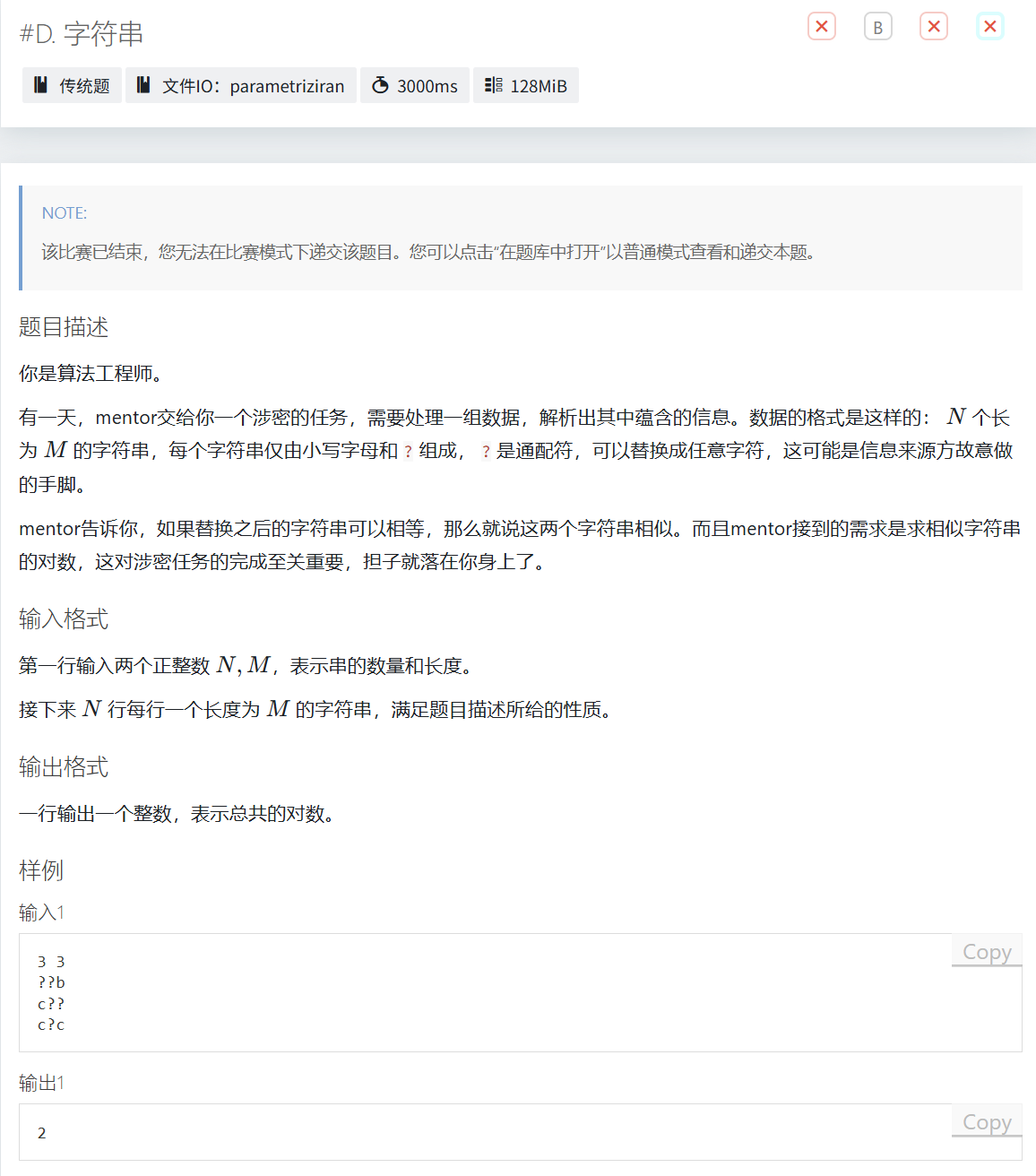
在这里插入图片描述

思路

回归后第一次遇到字典树的题，所以赛时没打字典树，而是对于m<=3（100%是N<=5e4，M<=6）的情况打了模拟。
考虑正解，根据题意我们可以建立一颗字典树，然后边输入边计算答案。

当我们向字典树添加一个字符串时，假设我们直接按照符号插入后，当我们在字典树上查询和它相似的字符串时，
对于’?‘符号，我们要搜索所有的小写字母和‘?’。
对于小写字母，我们搜索对应小写字母和’?'。

按照上述思路提交的话，只有75~90pts（波动取决于写的代码常数如何），剩下两个点TLE。
此时对于’？？？？？？'这种字符串，极端复杂度会达到 $27^6=387,420,489$ （虽然肯定要小得多，但能看出来可以造出来数据让代码TLE的）

这里提供两个优化，第一个是用空间换时间，优化成 $27^5$
我们对最后一位采取和上述不同的方式（或者说对字典树叶子节点
当我们向字典树添加字符串时，我们之前是直接添加，
现在变成对于’?'，把所有‘?‘和小写字母都添加一遍；对于小写字母，把对应小写字母和’?'添加一遍。
而查询的时候，最后一位直接加结果就行。
这么做会导致，插入复杂度从单次 $O (6) - > O (27) (或更小)$ ，查询复杂度（最差情况下）从 $O(27^6)->O(27^5)$
但是莫名其妙RE了一个点，仍然T了两个点，最后85pts ~~（比没优化还低~~
还有种思路是记忆化搜索，但是本人没写这个思路，我也只是想到了而已

代码实现（85pts带优化

#include <bits/stdc++.h>
#define intt long long
#define N 400005
#define debug(x) cout<<#x<<":"<<x<<" "<<endl;
#define re register 

using namespace std;
//using namespace __gnu_pbds;
int T,n,m,ans,cnt,num2[N];
struct tr
{
	int son[28];
}a[N]; 
char ch[10];
inline void yinsert()
{
	int p=0,u1;
	for(re int t=0;t<m-1;++t)
	{
		if(ch[t]=='?') u1=26;
		else u1=ch[t]-'a';
		if(a[p].son[u1]==0)
		{
			a[p].son[u1]=++cnt;
			p=cnt;
		}
		else p=a[p].son[u1];
	}
	int p1; 
	if(ch[m-1]=='?') 
	{
		for(u1=0;u1<=26;++u1)
		{
			p1=p;
			if(a[p].son[u1]==0)
			{
				a[p].son[u1]=++cnt;
				p1=cnt;
			}
			else p1=a[p].son[u1];
			++num2[p1];
		}
	}
	else
	{
		u1=ch[m-1]-'a';
		p1=p;
		if(a[p].son[u1]==0)
		{
			a[p].son[u1]=++cnt;
			p1=cnt;
		}
		else p1=a[p].son[u1];
		++num2[p1];
		
		p1=p;
		if(a[p].son[26]==0)
		{
			a[p].son[26]=++cnt;
			p1=cnt;
		}
		else p1=a[p].son[26];
		++num2[p1];
	}
	return ;
}
inline int yask(int p,int t)
{
	int sum=0,u1;
	if(ch[t]=='?') u1=26;
	else u1=ch[t]-'a';
	if(t==m-1)
	{
		return num2[a[p].son[u1]];
	}
	if(u1==26)
	{
		for(re int i=0;i<=26;++i)
		{
			if(a[p].son[i])
			{
				sum+=yask(a[p].son[i],t+1);				
			}
		}
	}
	else
	{
		if(a[p].son[u1]) sum+=yask(a[p].son[u1],t+1);
		if(a[p].son[26]) sum+=yask(a[p].son[26],t+1);
	}
	return sum;
}

int main()
{
	
//	freopen("parametriziran.in","r",stdin);
//	freopen("parametriziran.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int t=1;t<=n;++t)
	{
		scanf("%s",ch);
		ans+=yask(0,0);
		yinsert();
	}
	printf("%d",ans);
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}