蓝桥杯 算法提高 和谐宿舍2 （Python3 实现）（动态规划）

问题描述
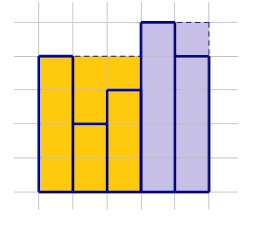
　　我的某室友学过素描，墙上有n张他的作品。这些作品都是宽度为1，高度不定的矩形，从左到右排成一排，且底边在同一水平线上。
　　宿舍评比就要来了，为了及格，我们决定买不多于m块的矩形木板，把这些作品和谐掉。要求木板也从左到右排成一排，且底边与作品的底边在同一水平线上。
　　在能够把所有作品和谐掉的前提下，我们希望这些木板的面积和最小，问最小面积和。

输入格式
　　第一行两个数n和m，表示作品数和木板数；
　　第二行n个数Hi，表示从左到右第i个作品的高度。
输出格式
　　一行一个数ans，表示答案。
样例输入
5 2
4 2 3 5 4
样例输出
22
数据规模和约定
　　对于30%的数据：1<=n，m<=10；
　　对于100%的数据：1<=n，m<=100，1<=Hi<=10000。

分析：
还是动态规划的题目，和之前做的“最大的算式”（步骤写的很详细）
很像。“最大的算式”比这个相对更直观一点，可以看一下那题的分析步骤。

下面看到我们现在的这一题，用列表嵌套列表来实现我们的动态规划数组dp，因为后面我们要找出最小值，所以我们给数组每个点赋值无穷，Python里面float(‘inf’)表示无穷。

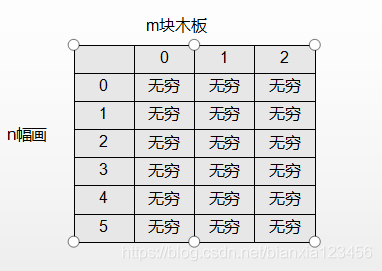
dp[i][j]就是表示有i幅画，j块木板所能实现的最小面积。
所以我们的第一列(用题目给的测试例子)：
dp[1][1] = 4 x 1 = 4
dp[2][1] = max(4,2) x 2 = 8
dp[3][1] = max(4,2,3) x 3 = 12
…
所以：

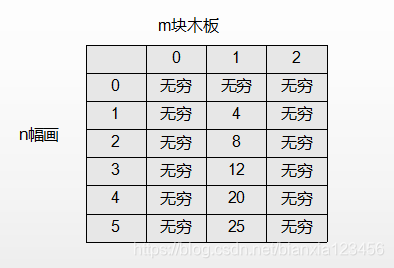
第二列就是我们要迭代的部分了：
画的数量一定要大于木板的数量，所以dp[1][2]肯定是没有值。
dp[2][2] = 4 + 2 = 6
dp[3][2] 就会有两种组合了：
1和（2,3）
（1,2）和3
dp[3][2] = min(4+max(2,3)x2,max(4,2)x2+3) = 10
…
通式来了：
dp[x][y] = min(dp[x][y], dp[z][y-1] + max(s[z:x])*(x-z) )
（1<=z<x）

while True:
    try:
        a = list(map(int, input().split()))
        n, m = a[0], a[1]
        s = list(map(int, input().split()))
        temp = []
        dp = [[float('inf') for i in range(m+1)]for j in range(n+1)]
        for i in range(1,n+1):
            dp[i][1] = max(s[:i])*i
        for y in range(2, m+1):
            for x in range(n+1):
                if x >= y:
                    for z in range(1, x):
                        dp[x][y] = min(dp[x][y], dp[z][y-1] + max(s[z:x])*(x-z) )
        print(dp[n][m])
    except:
        break

编程小白记录成长