辨析：分段函数是不是初等函数？

这是最近在上课的过程中作业题里面遇到的一个问题。

关于初等函数，《高等数学》（同济七版）中是这样子定义的：由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数，称为初等函数。
这个定义中，有两个需要注意的：(1) 有限次；(2) 可用一个式子表示(这句话很容易忽略，但是必不可少的)。

分段函数貌似不能用一个式子表达，所以不是初等函数。但是，存在这样的函数，它既可以用分段函数的形式表示，也可以用一个式子来表达，所以分段函数也有可能是初等函数。这个例子为绝对值函数：

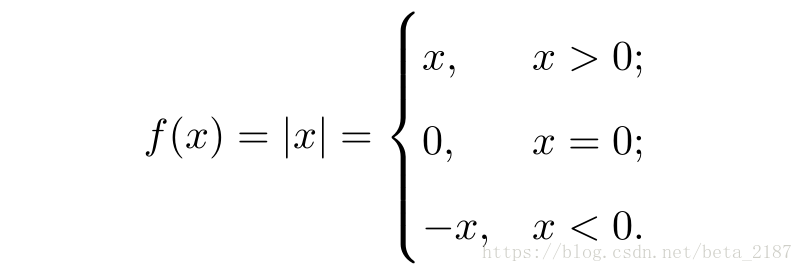
这个函数还可以写成
$$f(x)=|x|=\sqrt{x^2}.$$
根据初等函数的定义, 这是一个初等函数. 故函数$f(x)=|x|$可以写成分段函数，但它是一个初等函数.
所以结论就是：分段函数不一定是初等函数。