工业机器人快速校准方法

工业机器人快速现场校准方法研究

摘要

机器人校准是提高机器人精度的重要方法，针对工业机器人标定过程中多自由度参数辨识操作复杂的问题，本文基于激光跟踪仪系统和SA软件，提出了一种用于机器人连杆几何参数辨识的快速校准方法。该方法可直接测量机器人的连杆几何参数，无需复杂的参数辨识操作，因此更适用于工业现场的快速精确校准。最后，通过对HSR‐JR608机器人进行现场测试，验证了该方法的有效性。实验结果表明，该方法能够快速提升机器人的直线度。

关键词 —快速校准；激光跟踪仪；直线度精度

I. 引言

机器人校准是提高机器人位姿精度性能的主要方法，特别是基于运动学模型的机器人校准，能够显著提升机器人的位姿精度，从而满足工业应用需求。此类校准通常分为四个步骤[1]：1. 建立机器人的运动学模型及相应的误差模型；2. 对机器人进行位姿测量；3. 对相应的误差模型进行参数辨识；4. 进行误差补偿。其中，位姿测量与参数辨识过程较为复杂。尽管已有大量学者针对校准过程中的位姿测量开展了优化研究[2‐4], ，同时也增加了对机器人模型的前期研究，但对于多自由度机器人而言，由于机器人参数较多导致误差模型非常复杂，在参数辨识过程中需多次求解高阶矩阵的逆矩阵，造成时间和精力的浪费[5‐8]。对于某些应用领域，如弧焊，要求机器人具有较高的直线度，但对位姿精度要求相对较低。因此，面对如此复杂的校准流程，现场标定难以实施。为此，本文基于激光跟踪仪系统和SA软件，实现直接且快速的测量机器人的几何参数，获取实际几何参数，并在无需复杂位姿测量和大量高阶矩阵操作的情况下进行补偿，从而快速提高机器人的直线度，满足弧焊需求。

II. 校准原理

一般来说，工业机器人是一种多关节联动机构，其末端位姿由连杆的几何参数以及各关节（旋转关节）的旋转角或移动关节的位移距离决定。对于给定的机器人，末端位置P、关节角度 ș或位移距离S与其他几何参数L 之间存在如下关系：
F(, L) P θ = ᧤1᧥
F( s, L) P= ᧤2᧥
旋转角ș或位移距离S可通过编码掩模直接读取。理论上，机器人控制器中的连杆几何参数应与实际参数相等，但由于生产装配过程中存在各种偏差，导致机器人的理论计算模型与实际情况不符，从而引起末端位姿 P的偏差。通过拟合方法测量机器人轨迹上的点获得机器人的直线度，其精度由机器人末端的位置精度决定。

基于常用的D‐H模型，本文对六自由度机器人HSR‐JR608进行结构建模，该机器人具有六个旋转关节，如图1和图2所示。

文献[1,2,6,9]中关于建立D‐H模型的具体方法已有详细介绍，此处仅介绍D‐H参数。D‐H模型参数主要有四种：连杆长度a、连杆扭转角Į、连杆偏移量d和关节角ș。连杆长度ai定义为从前一个关节轴的xi-1轴到当前x轴的距离，沿xi轴方向；连杆扭转角Įi定义为从前一个关节轴的zi-1轴绕xi轴旋转到当前zi轴的角度，正方向为绕xi轴的正向旋转，且Į ∈(‐ʌ㧘ʌ]；连杆偏移量di定义为从xi-1轴到xi轴的距离，沿zi-1轴方向；关节角ș定义为从xi-1到xi的角点，且绕zi轴逆时针旋转，ș∈(‐ʌ㧘ʌ]。

如果将关节的坐标如上设置，则相连关节之间的变换关系可总结如下。
d) ) ( ) ( ( 1 1 i i-1 i i i i i i i Z Trans X Rot a X Trans Z Rot A 䯸 䯴 䯸 䯸 䯸䯵 − − • • • = α θ
» » » » ¼ º « « « « ¬ ª • » » » » ¼ º « « « « ¬ ª − • » » » » ¼ º « « « « ¬ ª • » » » » ¼ º « « « « ¬ ª − = 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 i i i i i i i i i i d c s s c a c s s c α α α α θ θ θ θ
0 0 0 0 1 i i i i i i i i i i i i i i i i i i i i i i i c c s s s ac c c s c c s as s c d α α α α α α − § · ¨ ¸ − ¨ ¸ = ¨ ¸ ¨ ¸ © ¹ ᧤3᧥
1 2 1 … n n F A A A A − = × × × × ᧤4᧥
对于它们而言，n是机器人的自由度。因此，根据正向运动学求解方法，可得到机器人末端执行工具在坐标系中的初始位姿。然而，连杆L的实际几何参数(și,Įi,ai,di)会与控制器中的理论参数不一致，因此末端位姿也会有偏差。因此可通过激光跟踪仪和SA软件测试机器人各关节的实际位置，并利用D‐H方法建立实际运动学模型。如图3所示：通过测试得到的实际结构模型与理论参数模型不重合（黑色部分为理论模型，红色部分为实际测试模型）

通过连杆几何参数的实际补偿，可以提高机器人的位置精度和直线度。

III. 标定过程

第一步：建立机器人基坐标系；将机器人置于初始位置，通过单步旋转轴1、轴2和轴4，采集各点，通过拟合得到轴1、轴2和轴4的轴线。根据基底的定义，轴1的轴线与基坐标系的Z轴重合，轴2的轴线与基坐标系的Y轴平行，轴4的轴线与X轴平行。由此可确定X‐Z平面，并将轴2的轴线投影到该平面上，再将子点投影到Z轴（即轴1的轴线）上，从而获得基坐标系的原点。因此，可构建机器人基坐标系。

第二步：测量机器人的位姿精度、重复性、直线度及其他性能指标；相对于机器人而言，目标球在整个过程中保持静止，因此可直接测量机器人的位姿重复性和直线度指标。关于位姿重复性的具体测量方法可以参考标准ISO 9283《工业机器人 操作型工业机器人 性能规范及其试验方法》。直线度测量可分为X轴、Y轴和Z轴方向的直线度测量，以及空间直线度测量，共四种直线度测量。

第三步：测量机器人的实际几何参数；根据机器人运动学D‐H模型的规律，通过激光跟踪仪和SA软件的图形配置进行检测与跟踪，可获得各轴对应的实际位置、夹角、连杆长度以及关节偏差。激光跟踪仪的精度在+/- 10ȝm以内，因此检测系统带来的误差可忽略不计，从而得到实际几何参数的误差。

第四步：参数补偿；将实际连杆长度、连杆偏移量以及第三步中测得的夹角数据导入机器人控制器，再次测量并反复进行补偿，直至机器人性能满足生产要求。

IV. 实验与结果分析

针对上述讨论，我们在主要用于焊接、打磨等领域 的六轴工业机器人HSR‐JR608上进行实验，通过标定可 显著提高直线度和精度，更有利于现场作业。测试系统 如图4所示，整个标定系统由工业机器人、激光跟踪仪和 反射靶标组成。我们选用徕卡AT901激光跟踪仪作为测 量设备，其具有高精度、动态连续测量等优点，可直接 获取机器人连续位姿，便于分析；SA软件是一款功能强 大的坐标测量软件，可与徕卡激光跟踪仪紧密集成。我 们逐一旋转机器人关节，并利用激光跟踪系统记录数据， 最终通过SA软件的图形拟合功能快速获得相应的关节轴 和旋转轴所在平面。操作界面如图5所示。

由于机器人系统默认第五轴与第六轴重合，且第六 关节仅与机器人姿态相关，因此只需测量和标定前五个 关节的几何参数。通过转动各旋转轴并获取连续点，可 得到每个旋转轴的回转半径。具体采集数据见表I。

表I. 数据采集

旋转axis	样本 Size	旋转角度(°)	实际半径 (毫米)	拟合误差 (mm)	理论半径 (mm)
1	467	180	791.06	0.027	789.5
2	160	120	842.02	0.02	856.66
3	145	120	641.57	0.012	656.18
4	90	270	147.33	0.006	147
5	80	180	147.19	0.014	147

基于D‐H模型，利用SA软件构建相应的平面和平面 或直线，测量对应平面或直线之间的距离和角度，从而获 得关节几何参数。如表II所示。

表II. D‐H参数在实际与标称情况下的对比

D-H	标称参数				实际参数
	a	d	Į	ș	a	d	Į	ș
1	150	0	90	0	149.78	0.01	89.97	0.05
2	570	0	0	90	570.41	0.034	0.042	89.31
3	130	0	90	0	130.13	0.15	90.04	-2.707
4	0	639.5	-90	0	0.15	641.213	-89.95	-0.64
5	0	0	90	0	0.014	0.052	90.035	0.003

机器人实际连杆的测量几何参数可输入至机器人控制 器。测量X轴、Y轴、Z轴方向变化的直线度、直线度变化 以及机器人的绝对定位精度。需找到在X轴、Y轴和Z轴方 向上具有不同距离的五条线。将其与空间中任意分布的 10条不同距离的直线进行比较。数据已在图6中显示：

a)

b)

c)

d)

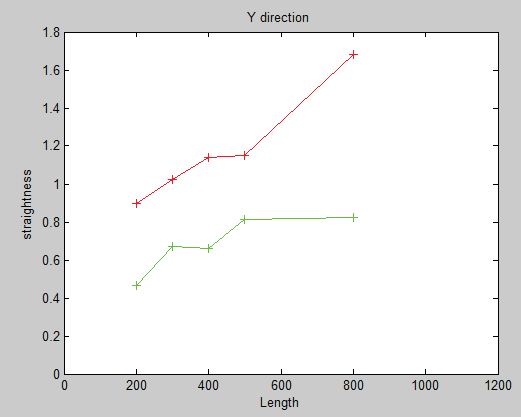
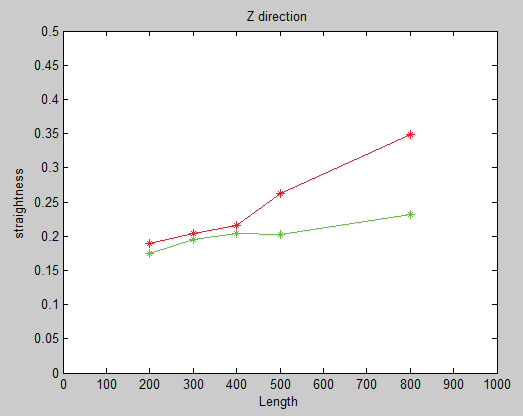
表III. X轴、Y轴、Z轴方向直线度变化

	校准前			校准后
	X	Y	Z	X	Y	Z
200	0.304	0.899	0.189	0.201	0.468	0.174
300	0.329	1.022	0.204	0.198	0.669	0.195
400	0.358	1.137	0.215	0.226	0.658	0.204
500	0.455	1.152	0.262	0.228	0.814	0.203
800	0.605	1.683	0.348	0.314	0.825	0.232

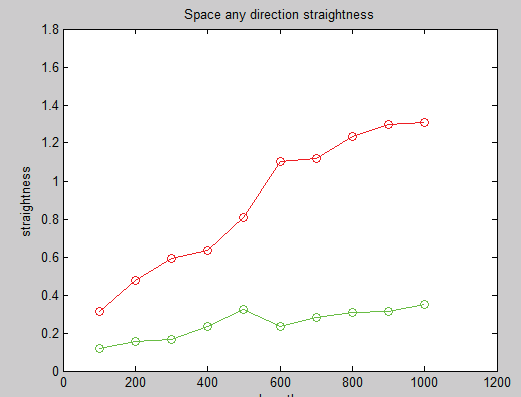
表IV. 空间任意方向直线度变化

长度	校准前	校准后
100	0.314	0.119
200	0.476	0.156
300	0.590	0.167
400	0.632	0.2331
500	0.807	0.324
600	1.103	0.232
700	1.121	0.279
800	1.235	0.308
900	1.299	0.311
1000	1.308	0.349

如表III和表IV所示，可以看出：通过检测机器人各连杆的实际几何尺寸和角度，并在机器人控制器中进行补偿，可快速提高机器人的直线度。X、Y、Z方向的直线度均有显著提升。其中，X方向由最大0.605mm降至0.314mm；Y方向由最大1.683毫米降至0.825毫米；Z方向由最大0.348毫米降至0.232毫米。并且从测试数据可知，随着直线距离的增加，标定效果更加明显。

V. 结论

本文通过激光跟踪工业点的快速测量以及数据拟合 与图形结构软件，可快速获取机器人的实际几何参数。将这些参数与运动学模型中的对应参数进行比较，得到偏差，并在机器人控制器中进行补偿以实现标定。该方法无需复杂的矩阵运算即可获得相应的误差结构，快速提高了机器人的直线度和定位精度，在机器人焊接和抛光等领域具有重要作用，同时也有助于实现快速现场标定。但由于测量误差和数据拟合误差的影响，标定结果存在一定局限性，因此当对机器人要求更为严格时，仍需进行系统标定。