第二章 线性模型

2.1 线性回归

2.1.1 什么是回归？哪些模型可以用于解决回归问题？

用于分析和建立因变量（Y）与一个或多个自变量（X）之间的关系。

• 线性回归：对异常值非常敏感（线性回归的目的是找到一条直线（或超平面）来最好地拟合数据点，使得预测值与实际值之间的误差最小化‌。）
• 多元线性（多项式）回归：如果指数选择不当，容易过拟合
• 岭回归：通过在损失函数中加入 L2 正则化项来防止过拟合。
• Lasso回归：通过 L1 正则化项进行特征选择，可以将某些系数压缩为零。
• 弹性网络回归：结合了 L1 和 L2 正则化，适用于特征数量多且相关性强的情况。

2.1.2 线性回归的损失函数为什么是均方差？

均方差损失函数由于其数学性质和计算简便性，仍然是线性回归中最常用的损失函数。
为了减少均方误差（MSE）对异常值的敏感性，可以考虑以下替代方案或改进方法：

1. 使用其他损失函数

• 平均绝对误差：MAE计算预测值与真实值之间绝对误差的平均值，不会对异常值进行平方放大，因此对异常值不敏感。
• Huber损失：Huber损失是一种结合了MSE和MAE优点的损失函数。它对小误差使用平方项，对大误差使用线性项，从而在保持MSE的平滑性的同时减少对异常值的敏感性。
• 截断均方误差：通过设定一个阈值，限制极端误差的影响，从而减少异常值对MSE的影响。

2. 数据预处理

• 去除或修正异常值：在数据预处理阶段，通过异常值检测和清洗，剔除或修正那些可能影响模型性能的异常值。
• 标准化或归一化：对数据进行标准化（Z-score）或归一化处理，使数据分布更加均匀，减少异常值的影响。

3.正则化

• 在损失函数中加入正则化项（如L1或L2正则化），可以防止模型过拟合，同时增强模型对异常值的鲁棒性。

2.1.3 什么是线性回归？什么时候使用它？

利用最小二乘函数自变量和因变量线性关系进行建模。
（1） 自变量和因变量呈直线分布
（2） 因变量呈正态分布
（3） 因变量数值之间独立
（4） 方差是否齐性

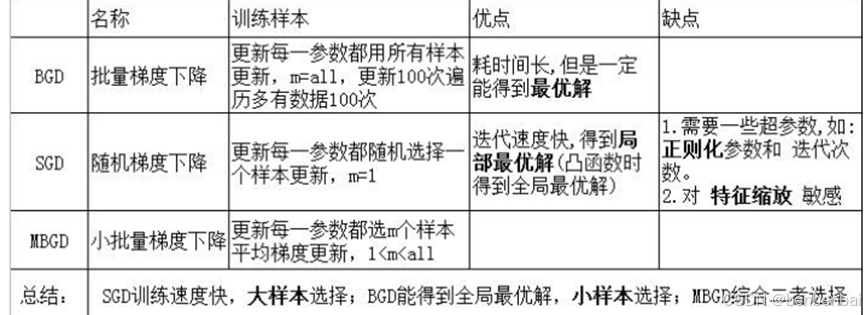
2.1.4 梯度下降？SGD的推导？

2.1.5 什么是最小二乘法？

通过最小化误差的平方和来寻找数据的最佳函数匹配。

2.1.6 常见的损失函数有哪些？

（1）0-1损失
（2）均方差损失MSE
（3）平均绝对误差MAE
（4）分位数损失：分位数回归可以通过给定不同的分位点，拟合目标值的不同分位数；
实现了分别用不同的系数控制高估和低估的损失，进而实现分位数回归。
（5）交叉熵损失
（6）合页损失：一种二分类损失函数，SVM 的损失函数本质： Hinge Loss + L2 正则化
合页损失的公式如下：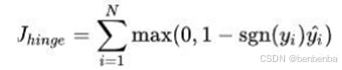

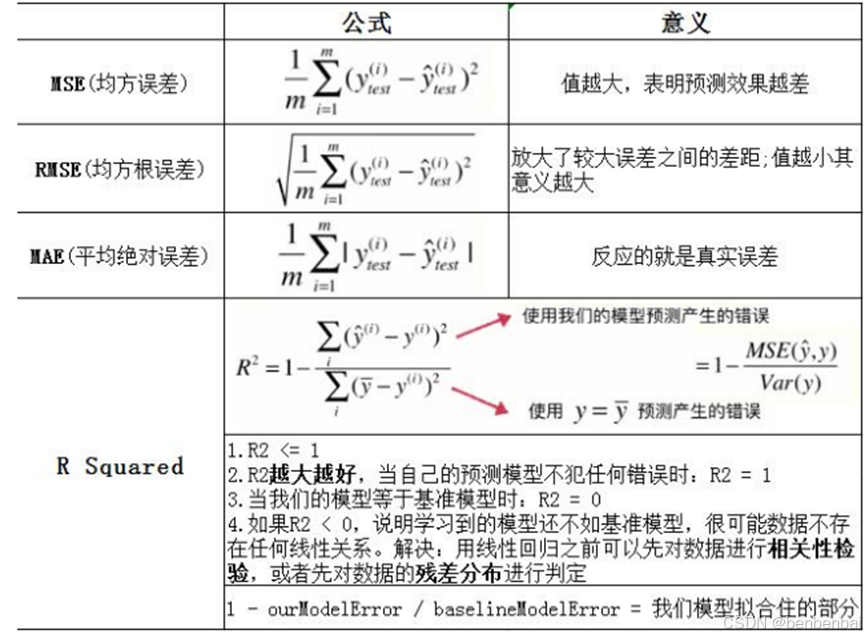
2.1.7 评估回归模型的指标？

R Squared 是评估线性模型的最好指标。

2.1.8 梯度下降法找到的一定是下降最快的方向吗？

不一定，它只是目标函数再当前点的切面上下降最快的方向。
在实际执行中，牛顿方向（考虑豪森矩阵）才一般被认为是下降最快的方向，可以达到超线性的收敛速度。梯度下降类的算法收敛苏苏一般是线性甚至次线性的（在某些带复杂约束的问题）

2.1.9 MBGD需要注意什么？

如何选择m？m一般取2的幂次方才能充分利用矩阵运算操作。
一般会在每次遍历训练数据之前，先对所有的数据进行随机排序，然后在每次迭代时按照顺序挑选 m 个训练集数据直至遍历完所有的数据。

2.1.10 什么是正态分布？为什么要重视它？

正态分布，也称为高斯分布，其数学表达式为：

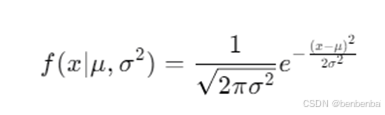
 其中，μ 是分布的均值（期望值），表示数据的中心位置；sigma是标准差， sigma^2 \是方差，它们决定了分布的离散程度。当 μ = 0 且 sigma = 1  时，正态分布被称为标准正态分布。

从直观上理解，正态分布的图形是对称的，数据在均值附近聚集得最密集，随着距离均值的增加，数据出现的概率逐渐减小。例如，人的身高、考试成绩等很多自然现象和人类活动产生的数据都近似服从正态分布。

在机器学习中重视正态分布的原因

• 许多机器学习算法在建模时假设数据服从正态分布。例如，在线性回归中，通常假设误差项（即观测值与模型预测值之间的差异）服从正态分布。这种假设使得模型的参数估计更加合理。因为如果误差项是正态分布的，根据最小二乘法原理，通过最小化误差的平方和来估计参数，可以得到最优的参数估计值。当数据满足正态分布假设时，模型的统计性质（如置信区间、假设检验等）更容易被理解和分析。
• 正态分布的数学性质良好，具有许多方便的性质。例如，正态分布的线性组合仍然是正态分布。如果 \X 和 \Y 是两个独立的正态随机变量，那么 aX + bY （其中 a 和 b 是常数）也是正态分布的。这使得在机器学习中进行复杂的数学推导和计算变得相对容易。在贝叶斯统计中，当先验分布和似然函数都服从正态分布时，后验分布也是正态分布，这种性质简化了贝叶斯推断的过程。
• 正态分布的尾部概率很小。在机器学习中，如果数据服从正态分布，那么可以利用这一性质来检测异常值。例如，假设数据服从均值为 μ标准差为 sigma 的正态分布，那么数据落在（μ± 3*sigma ) 范围之外的概率只有约 0.27%。如果某个数据点超出了这个范围，就可以认为它是异常值。在信用卡欺诈检测、网络入侵检测等场景中，这种基于正态分布的异常值检测方法非常有用。
• 在机器学习的数据预处理阶段，正态分布是一个重要的参考标准。如果数据不符合正态分布，可以通过数据转换（如对数变换、Box - Cox变换等）使其接近正态分布。例如，对于右偏分布的数据（如收入数据），取对数后可以使数据分布更加接近正态分布。这种数据转换有助于提高模型的性能，因为很多算法对数据的分布有一定的要求。此外，在特征工程中，正态分布的特征往往更容易被模型理解和利用。

如何检查变量是否遵循正态分布？

在实际应用中，通常会结合图形方法和统计检验来判断数据是否服从正态分布。图形方法可以提供直观的视觉信息，而统计检验可以提供量化的证据。如果数据量较大，可以使用统计检验；如果数据量较小，可以使用图形方法。在某些情况下，即使数据不服从正态分布，也可以通过数据转换（如对数变换、Box-Cox变换等）使其接近正态分布，从而满足机器学习算法的假设。
说明：统计检验
o Shapiro-Wilk检验：Shapiro-Wilk检验是一种常用的正态性检验方法，适用于样本量较小的情况（通常小于5000）。该检验的原假设是数据服从正态分布。如果检验的p值小于显著性水平（如0.05），则拒绝原假设，认为数据不服从正态分布。
o Kolmogorov-Smirnov检验：Kolmogorov-Smirnov检验是一种非参数检验方法，可以用于检验数据是否服从任意给定的分布，包括正态分布。该检验的原假设是数据服从正态分布。如果检验的p值小于显著性水平（如0.05），则拒绝原假设，认为数据不服从正态分布。
o Anderson-Darling检验：Anderson-Darling检验是一种用于检验数据是否服从正态分布的非参数检验方法。该检验的原假设是数据服从正态分布。如果检验的p值小于显著性水平（如0.05），则拒绝原假设，认为数据不服从正态分布。

2.1.11 如何建立价格预测模型？

建立价格预测模型通常包括以下几个步骤：

1. 数据收集与预处理

• 数据来源：从金融网站、API接口或公共数据集获取历史价格数据。
• 数据清洗：删除无关列（如成交量、调整后价格等），处理缺失值和异常值。
• 数据归一化：将价格数据进行标准化处理，例如使用Min-Max标准化。
• 特征工程：选择或构造特征，如移动平均线（MA）、相对强弱指标（RSI）等。

2. 模型选择与构建

• 时间序列模型：如ARIMA、Prophet，适用于处理时间序列数据。
• 深度学习模型：如LSTM（长短期记忆网络）或CNN-LSTM，能够捕捉时间序列中的复杂模式。
• 混合模型：结合技术指标和文本特征（如新闻情感分析）构建综合模型。

3. 模型训练与验证

• 训练集与测试集划分：将数据按时间顺序划分为训练集和测试集。
• 损失函数与优化器：使用均方误差（MSE）作为损失函数，Adam优化器进行训练。
• 超参数调优：调整模型的隐藏层维度、学习率等超参数。

4. 模型评估与优化

• 性能指标：计算均方根误差（RMSE）评估模型性能。
• 模型解释：使用SHAP值或LIME解释模型预测结果。

5. 结果可视化

• 绘制预测结果与真实值的对比图，展示模型的预测效果。

价格是否服从正态分布？

价格本身通常不服从正态分布，尤其是股票价格。价格数据往往具有以下特点：

• 非负性：价格不能为负。
• 右偏分布：价格分布通常右偏，存在长尾。
• 波动性：价格波动具有自相关性和异方差性。
  然而，价格的对数收益率（即对数差分）通常更接近正态分布。对数收益率的计算公

是否需要对价格进行预处理？

是的，价格数据通常需要进行预处理，原因如下：

1. 归一化：将价格数据缩放到一定范围内（如[-1, 1]或[0, 1]），以提高模型的训练效率。
2. 对数转换：对价格取对数可以稳定方差，减少数据的右偏性。
3. 差分处理：通过计算差分（如对数差分）将非平稳时间序列转换为平稳时间序列。
4. 特征构造：构造技术指标（如MA、RSI）或引入外部特征（如新闻情感分析）。
   通过这些预处理步骤，可以显著提高价格预测模型的性能和稳定性。