神经网络预测磁层环境

第十一章 人工神经网络用于确定磁层条件

1 引言

指定和预测地球内磁层环境状态的能力一直是空间科学的长期目标，这一点在许多社区“路线图”文件中都有所体现，例如最近的美国国家研究委员会十年调查（National Research Council，2013年）或国家空间天气行动计划（National Science and Technology Council，2015年）。磁层环境包含多种组成部分，例如电离层、大尺度电场和磁场、等离子体波、电子以及从冷能量（<1电子伏特）到超相对论性（>5兆电子伏特）能量范围的各种离子。由于这些组分的行为通常难以一概而论，它们可能受到太阳风等外部因素和各种不稳定性等内部因素的驱动，并且还可能以复杂的方式相互耦合，从而产生常常出人意料的行为。

科学界用于特定化和预测的传统方法是深入研究系统的物理基础，理解所涉及的物理过程，并（希望）建立一组方程，以模拟系统的时空演化。确实，空间物理领域的许多研究人员正在追求这一目标，致力于开发基于第一性原理的基于物理的模型，以模拟内磁层环境的某些方面（例如，沃尔夫等人，1991；托福莱托等人，2003，2004；约尔达诺娃等人，2008，2010；王等人，2004；威尔特伯格等人，2004；古德里奇等人，2004；彭布罗克等人，2014；格劳尔特等人，2014；马等人，2015；什普里茨等人，2015；苏等人，2010；涂等人，2013）。基于物理的模型的主要优势在于它们采用基本的物理原理，因此（希望）在推演此前未观测到的情况时仍然有用。其缺点是这些模型通常较为复杂，计算量大，并且不可避免地无法在模拟中包含所有物理过程（要么因为模型的计算成本过高，要么因为——正如经常发生的那样——控制特定系统的物理过程尚未被完全理解或识别），这可能导致错误的结果。

在描述与预测问题上采取完全相反的方法，内磁层的状态可以通过将某一特定物理量（通常由卫星或其他观测平台在数年内收集）直接绘制在平面或三维空间中来确定，通常使用某些控制参数进行粗略的参数化。例如，Meredith 等人 (2012) 基于动力学探索者（DE1）卫星、综合释放与辐射效应卫星（CRRES）、星簇1号、双星计划TC1以及亚暴期间事件与宏观相互作用时间历史（THEMIS）卫星的观测数据，将内磁层中哨声模合唱波的强度按地磁极光电集流（AE）指数的三个范围（分别代表平静、中等和活跃状态）进行参数化绘图。这种方法提供了一种真实但静态且经过统计平均的产品。它有助于大致了解所绘物理量的空间分布和强度范围，但无法捕捉该物理量在逐个案例上的变化，也无法反映磁层中的时空变化条件。继续以上述例子为例，Meredith 等人(2012) 得到的合声波分布可用于计算描述高能电子散射与加速的扩散系数，而这些系数又可进一步用于建模给定磁暴期间辐射带电子的演化（例如，Horne 等人，2003）。然而，由于哨声波分布被平均化，所得到的辐射带动力学也将仅产生平均磁暴响应。

近年来，一些专门的数据驱动模型通过在不同地磁活动水平下对数据进行函数拟合而开发出来。例如，Orlova 等人 (2014) 建立了两个地方时扇区中等离子体层嘶嘶声强度的模型，并使用线性逐步回归方法计算了关于L壳、纬度和Kp指数的二次多项式的权重系数。该方法的一个扩展被Kim 等人(2015) 所采用，他们针对两个纬度范围内的哨声波强度，在每2小时磁地方时（MLT）区间内拟合高达七次多项式，其驱动因子为太阳风条件或地磁指数。尽管这些函数拟合使模型更具灵活性和动态性，但所使用的拟合函数形式仅适用于当前参数，若要预测不同的参数，则不可避免地需要采取新的方法。

显然，基于物理的模型和平均统计分布在描述和预测内磁层环境方面各有优缺点。一个理想的模型可能结合这两种方法的优点，既利用数据驱动的统计分布图的简洁性和真实性，又具备类似基于物理模型的时间和空间变化能力（但理想情况下避免这些模型高昂的计算成本）。这本质上是本章的主要内容。

本章所述的建模方法依赖于使用人工神经网络（ANN），特别是“深度”神经网络（即具有多个隐藏层的ANN）。该方法旨在避免为每一个新模拟量设计新的函数拟合形式所带来的困难，转而提出一种通用的建模技术，能够在不需要事先知道函数形式的情况下，基于卫星数据指定内磁层中的任意给定量。该模型通常由一个或多个地磁指数（和/或太阳风参数）的时间序列驱动，其思路是让人工神经网络自身从输入数据中挑选出最重要的元素，并在第一层中将输入重新组合成一组对描述模型动态更为优化的新特征集。在第2节中，我们对人工神经网络进行简要回顾。我们在第3节中以电子数密度为例说明我们的方法，并在第4节中展示更高级的应用。最后在第5节中总结并讨论此类模型如何有效地应用于空间天气预报。

2 人工神经网络简要回顾

人工神经网络（ANN）的起源可追溯到麦卡洛克和皮茨（McCulloch and Pitts）于1943年提出的分析模型，该模型旨在当细胞膜中的化学阈值被超过时，对生物神经元的放电过程进行数学模拟。麦卡洛克和皮茨（MP）神经元是一种非常简单的模型：给定一个长度为N的输入向量x = [x1, x2, …, xN]，以及一个同样长度的权重向量w = [w1,w2, …, wN]，计算它们的点积 h = w·x。

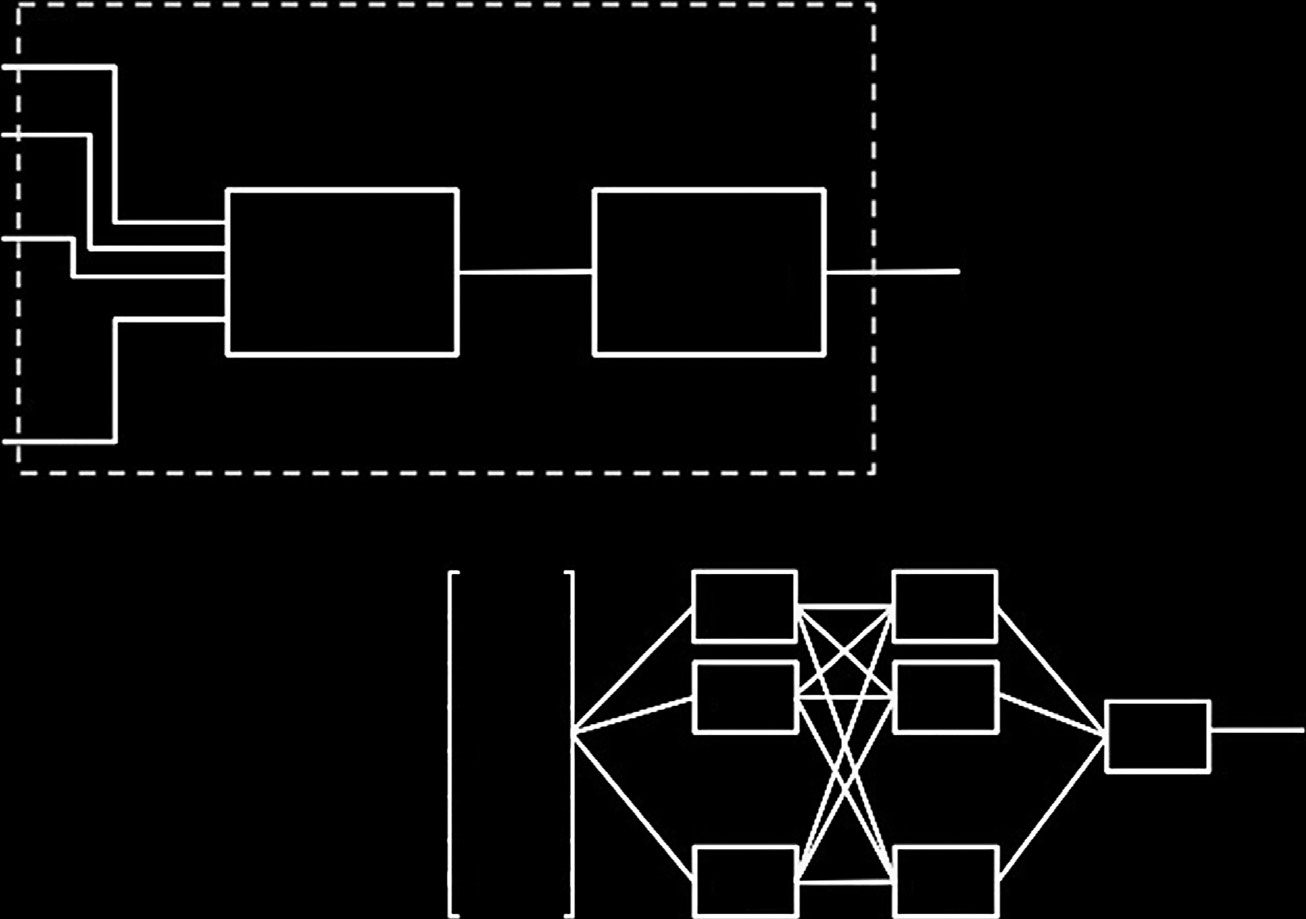
如果输出超过某个阈值T，MP神经元就会“激活”，即给出1的输出值，否则输出0（例如，Marsland，2009年，第14页）。MP神经元在图1A中以图形方式展示，其中函数a(h)被称为“激活函数”，并被选为海维赛德阶跃函数，即

$$
y = a(h) = \begin{cases}
1 & \text{if } h \geq T \
0 & \text{if } h < T
\end{cases}
$$

输入向量 x 可以很容易地输入到任意数量的单个神经元中，每个神经元根据其特定选择的权重产生各自的输出，从而不再是一个单一的输出值 y，而是生成一个输出向量，y(1)=[y11, y21,…, yM1]，假设有 M个单个神经元。这个输出向量 y(1)随后可被视为一个新的输入向量，并作为输入传递到一组新的（或称为“层”）神经元中，从而产生下一个输出向量 y(2)=[y12, y22,…, yP2]，假设第二层有 P个单个神经元。可以添加任意数量的层，每一层依次将前一层的输出作为自己的输入，且每层中可以放置任意数量的单个神经元。这一组相互连接的神经元，包括层数、每层中的神经元数量（以及所选的激活函数和神经元之间的连接方式，此处暂不讨论），统称为“神经网络”，并在图1B中以图形方式展示，其中每个方框对应如图1A所示的单个神经元。在图1B中，输入向量 x通常被称为“输入层”，中间的第1层和第2层（分别包含 M和 P个神经元）被称为“隐藏层”，而最后一层L被称为“输出”层。在此架构中，每个神经元的输出都成为下一层每个神经元的输入，信息从左到右流动，没有环路或反馈，因此这种架构被称为全连接前馈神经网络。添加的层数和每层的神经元越多，神经网络的复杂性和能力就越强，从而能够建模日益复杂的函数。然而，自由参数的总数（即所有神经元的权重）也会随着每一层的增加而显著增长，因此应谨慎选择神经元的总数。

选择神经网络中所有权重的合适值的过程称为“训练”，通常涉及一个迭代的数值过程。选取大量具有已知输入和输出的样例（称为“训练集”），对每个输入样例，神经网络使用一组任意选定的权重产生输出y，然后将其与已知输出（称为“目标”t）进行比较，计算y与t之间的误差，并利用该误差在下一次训练迭代中调整神经网络的权重。此过程在整个训练集上重复多次，直到神经网络在给定已知输入时产生“正确”的输出，即输出在目标的某个可接受误差范围内。举一个简单的例子，考虑一个设计用于识别 16× 16‐像素黑白图像中数字的神经网络。输入向量x由图像的所有像素组成，排列成长度为N= 256的单列向量，输出y在识别出相应数字（例如图像对应数字“9”）时给出一个正的“标志”值（例如y= 1），否则给出负的“标志”值（例如y= 0）。由于x的长度为N= 256，第一层中的每个权重向量w将具有类似的长度，如果有M= 10个神经元在第一层，则自由参数的总数将为 256 × 10=2560。如果引入另一层，则第二层的每个神经元将有10个权重，因此如果第二层有P= 20个神经元，则神经网络中将另有∼10×20= 200个自由参数。这样，神经网络中自由参数的总数可以迅速上升到数百至数千（有时数百万，如果考虑更大的图像），因此当训练神经网络时，训练集中样例的数量必须远大于自由参数的数量，至少大10倍，最好更多，也就是说，应向神经网络提供>30,000张图像，每张图像都标记为“0”或“1”，表示该图像是否显示了数字“9”。

然后迭代调整神经网络的权重，直到训练集中的图像被正确分类，之后原则上，该网络应能够对样本外数据（即它以前未见过的图像）进行分类，并判断它们是否显示了数字“9”。

困难在于“训练”模型，即通过算法确定权重系数的最优集合W，以产生“正确”的输出。首个能够进行算法训练的神经网络由一组互连的MP神经元构成，被称为“Mark 1感知机”，这是一台定制机器，旨在对由400个光电管阵列组成的图像（类似于前面的例子）执行图像识别（Rosenblatt，1957）。尽管感知机算法是同类中的首个方法，并且大多数情况下能产生准确结果，但对于某些分类问题，它仍存在收敛和不稳定性问题，主要与海维赛德阶跃函数固有的急剧不连续性有关。

直到Rumelhart 等人（1986）开发出一种通用算法来训练神经网络，这几乎又花了三十年时间。该算法被称为“反向传播算法”，因为它能够将神经网络预测值与目标值之间的误差反向传播，并利用这些信息调整内部权重。该网络使用逻辑函数f(y)=(1+ e−y)−1作为其激活函数，该函数在y的绝对值很大时的行为与海维赛德阶跃函数相同，即分别趋近于0和1，但在y ∼ 0附近具有光滑且可微的优势。反向传播算法通常被认为是神经网络迅猛发展的主要原因，这一趋势一直延续至今（尽管在20世纪90年代初期由于计算速度和内存不足以应对当时的问题而有所放缓，但在随后的二十年中已迅速赶上并超越）。

在结束本节简要回顾时，我们指出，现代人工神经网络可以被视为一种对高维向量的复杂非线性函数进行建模的通用方法，事实上已证明在包含足够数量神经元的情况下，它能够作为任何平滑函数的通用逼近器（Hornik等人，1989；Cybenko，1989）。具有两个或更多隐藏层的人工神经网络如今被称为“深度”神经网络，并已被证明比“浅层”网络更高效（Bengio，2009），更重要的是，深度网络能更好地进行预测，因为它们能够将输入参数集合重新组织为比最初提供给人工神经网络的输入更优或更高效的特征集（Hinton等人，2006）。

提供给人工神经网络的输入向量可以有多种形式，例如：（i）静态图像中的像素，如前面简单的图像分类示例中所示；（ii）股市每日收盘价的时间序列，人工神经网络的目标是预测下一天的收盘价；（iii）在空间某一区域上获取的空间值，人工神经网络的目标是预测空间另一区域上某函数的值；（iv）描述一个人的参数，人工神经网络的目标是就其健康状况、可保性和信用状况做出决策；或（v）上述任意组合。在本章中，我们的目标是预测一组值的时空分布，问题概述及所采用的方法将在接下来进行描述。

3 方法论与应用

我们旨在解决的通用问题可表述如下：给定某一物理量Qi在时间ti和位置ri的一系列测量值，其中i = 1, …, N，且N为一个“较大”的数值，需确定在时刻t该物理量Q在模型域内每一点r处的空间分布，并使该空间分布随时间演化。为了说明我们的技术方法，本文展示了一个应用实例，其中选取的物理量Qi为等离子体密度Ne，该密度是根据三颗THEMIS探测器（A、D和E）的航天器电位推断得出的（Angelopoulos, 2008），所用方法来自李等人（2010）。该数据集的时间范围从2008年6月1日持续到2014年10月31日，并被处理为5分钟平均值，在进行一些基本的数据清理（例如剔除探测器处于地球阴影中时的异常数据点）后，共得到 ∼106个数据点。

为了将数据组织成一个动态模型，我们必须选择一个或多个输入参数的时间序列来对数据进行回归，这些时间序列将作为合适的预测因子并包含足够的信息，以解释数据的各种行为。例如，我们可以仅使用前5小时的SYM‐H指数（同样为5分钟采样间隔，共60个数据点）作为唯一的预测因子，因为该指数简单，可通过OMNI数据库（ftp://spdf.gsfc.nasa.gov/pub/data/omni/high_res_omni/）轻松获取，并且已被先前的研究人员用于驱动更复杂的等离子体层‐电离层模型（例如，Huba 和 Sazykin，2014），也就是说，它应包含足够的信息，可作为冷等离子体密度的预测因子。我们对SYM‐H的选择并非唯一，也可以同样使用其他地磁指数，如AE或Kp（适当下采样至5分钟采样间隔），或太阳风参数。然而，由于不同的地磁指数彼此之间高度相关（Borovsky，2014），并且已经反映了太阳风中的驱动条件（例如，参见关于耦合函数的文献，总结于Newell 等人（2007）和 McPherron 等人（2015）），因此SYM‐H指数的时间序列包含了作为预测因子所需的信息，可用于纳入磁暴效应对等离子体层的影响。此外，太阳风数据往往存在大量数据缺失，这会导致我们丢失许多数据点，而SYM‐H则可在长时间段内获得且无数据间隙。

所得设计矩阵 X 和目标矩阵 T 可表示为：

$$
X = \begin{bmatrix}
SYM-H_{i-60} & \cdots & SYM-H_i & L_i & \cos\varphi_i & \sin \varphi_i \
\vdots & \ddots & \vdots & \vdots & \vdots & \vdots \
SYM-H_{N-60} & \cdots & SYM-H_N & L_N & \cos\varphi_N & \sin \varphi_N
\end{bmatrix}, \quad T = \begin{bmatrix}
Q_i \
\vdots \
Q_N
\end{bmatrix}
$$

其中，角度 φi 表示磁地方时角（MLT/24×2π)，Li 表示卫星在时刻 ti 的 L壳，以及航天器在该时刻观测到的相应电子密度 Qi，以及 i= 1… N，使得 X 和 T 均具有 ∼106 行和 63 列。我们使用正弦和余弦函数以确保在子夜边界处的连续性。为了说明目的，我们仅考虑磁赤道面内的电子密度，但可通过在设计矩阵 X 中增加一列表示卫星在时刻 ti 的纬度 λi，将模型直接扩展到三维（如下一节所示）。

现在的问题是如何创建一个模型，以给定的设计矩阵 T来预测X。这个问题可以通过多种技术来解决，基本上所有处理回归的机器学习技术都是为了解决此类问题而设计的（例如，Marsland，2009年）。最简单的方法是通过创建一组权重A=[a1… am]T来建立一个线性模型，使得XA= T，并获得普通最小二乘解，即：A=(X TX) −1XTT，但不能保证我们目标量（电子密度）的响应一定是线性的，实际上，它很可能是输入的非线性函数。

本章介绍的技术基于前一节所述的人工神经网络，是一种对复杂非线性函数进行建模的强大且通用的方法。例如，Bortnik etal.（2016）所使用的人工神经网络架构包含一个具有 63个特征的输入层（如前一节所示）、两个隐藏层，第一层和第二层分别包含10个和20个神经元，每层均采用相同的S型激活函数，以及一个输出层。我们采用具有两个隐藏层的人工神经网络，因为这是最浅的“深度”网络，即从意义上讲，其隐藏层数量超过一层。

层。每个隐藏层中的神经元数量是随意选择的，既没有尝试优化性能，也没有力求构建出最简化的网络。

通常情况下，第一层将输入参数重构为其自身的最优特征集，通过在此层中选择10个神经元，我们实现了数据压缩，即将系统的维度从63减少到10。这一点在直觉上是合理的，因为63个输入参数并非全部独立，特别是SYM‐H的60点、5小时时间历史可以通过仅提取相关信息显著降低维度；例如，可以寻找SYM‐H下降的范围和强度、持续时间等特征。以我们的密度预测示例而言，人们可能会猜测最重要的特征，并直接将这些特征作为输入提供给人工神经网络，但在一般情况下，我们未必知道输入时间序列的哪些方面包含最相关的信息，因此最好让人工神经网络在前几层中自行构建其最优特征集。我们的人工神经网络第二层包含20个神经元，在这一层中，最优特征被重新组合以捕捉系统的物理行为。原则上，“深度”人工神经网络通常不需要超过两个隐藏层，因为这种架构应能够逼近任何平滑的函数映射（参见 Marsland，2009年，第3节3.3.3）。

为了训练神经网络，数据被分为三组：包含70%样本的训练集、包含15%样本的验证集以及包含剩余15%样本的测试集。训练集的数据点与每个数据点对应的SYM‐H时间序列一起用于训练人工神经网络（Bortnik et al.，2016），其中使用缩放共轭算法进行训练（Marsland，2009）。人工神经网络的训练持续进行，并在每个时间步计算预测值与观测值之间的均方根误差，针对所有三个数据集分别计算。判断神经网络“优劣”的方法有多种，但本文采用的方法是关注网络的泛化能力，因此我们持续训练，直到验证集的均方根误差在连续多个时间步内不再改善为止（此处我们任意选择六个时间步）。需要注意的是，验证集本身不直接参与训练，因此是独立的（除了用于决定训练停止的时机）。测试集则是一组完全独立的样本，用于检验人工神经网络的泛化能力和性能表现。通常情况下，必须注意数据在训练集、验证集和测试集之间的划分方式，因为这可能会影响模型的整体性能。数据可以逐个样本随机分配到三个集合之一，也可以先划分为较大的块（例如天或周），再将这些块随机分配到各集合中，或者将整个数据集划分为三个互不重叠且时间上连续的块，以避免样本间出现任何形式的交叉相关性。在Bortniket al.（2016）的研究中，数据被划分为连续的时间段，而在Chu et al.（2017a，b）中则是随机分配的。在实际操作中，训练人工神经网络模型时，我们通常会同时使用这三种数据划分方法及其各种混合形式来训练多个模型，从而更准确地评估模型的真实性。迄今为止，我们发现无论采用哪种数据划分方法，模型性能都相似，因此本章展示的结果为简化和清晰起见采用了随机样本划分方式，但总体而言，我们建议实践者在训练其人工神经网络模型时尝试多种数据划分方法，以获得更准确的性能估计。

3.1 DEN2D模型

上一节中描述并由Bortniket al.（2016）提出的基线人工神经网络模型主要考虑了由 SYM‐H指数衡量的磁暴效应所主导的等离子体层动力学。然而，等离子体层动力学的整体范围比预期更为复杂，因为它还与电离层和磁层相互作用。等离子体层的下部通常与上层电离层处于扩散平衡状态；而等离子体层的上部或等离子体层顶则受磁层对流强度和变化性的控制。

为了研究来自不同过程的贡献，通过引入更多代表这些过程的地磁指数，显著扩展了赤道面上二维等离子体密度（DEN2D）的人工神经网络模型（Chu etal.，2017b）。因此，DEN2D模型不仅包含了由SYM‐H指数衡量的磁暴效应，还包括了由F10.7（太阳极紫外）指数衡量的电离层效应，以及由AL指数（即AE地磁扰动的下包络线）衡量的磁层效应。有关DEN2D模型的详细描述，请参见Chu et al. （2017b）。我们注意到，此处我们试图通过对等离子体密度特定的适当输入进行极致优化，以捕捉仅使用SYM‐H作为输入的简单模型未能解释的最后几个百分点的方差。

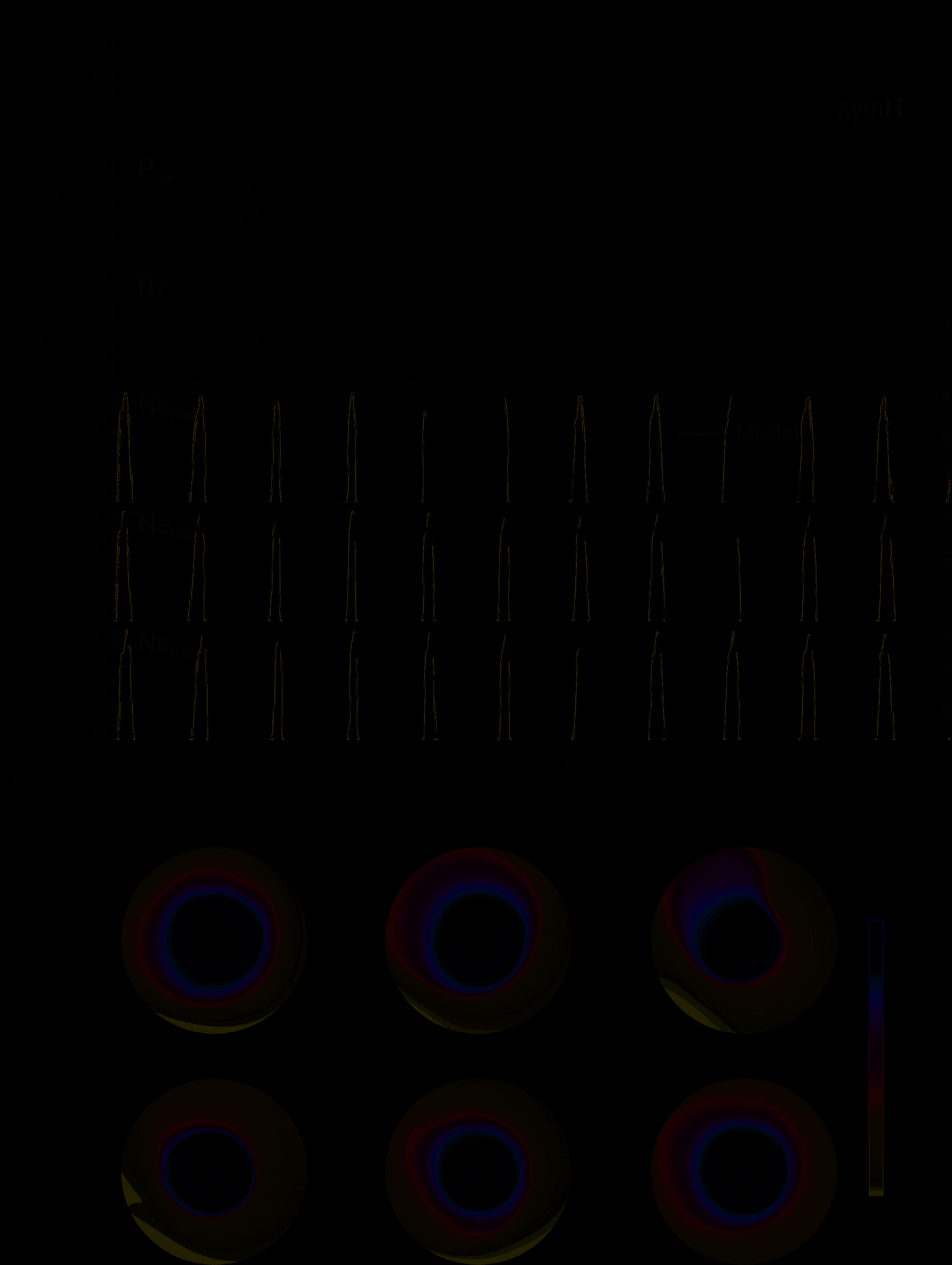
为了说明其功能范围，将DEN2D模型应用于2011年2月4日发生的一次中等强度风暴事件，如图2所示。太阳风动压的突然增加表明约在03世界时到达了行星际激波。随后，磁暴约在 17世界时开始，这由SYM‐H指数的变化体现，该指数达到最低值−66 nT，然后在接下来的几天内缓慢恢复。底部三个面板显示了THEMIS探针A、D和E的观测（黑色）与模拟（蓝色）电子密度剖面之间的对比。总体而言，在整个时间区间内均发现了良好的一致性，表明 DEN2D模型能够捕捉到等离子体层时空动力学的基本行为。如果这些等离子体层动力学确实被人工神经网络的内部权重正确捕获并再现，那么等离子体层电子数密度应在整个空间域内表现正确，并随时间真实演化，实际情况确实如此。为了展示这一能力，我们重建了同一风暴事件期间赤道面上的电子密度分布，其中图2g–l展示了全球演化的几个快照。在磁暴开始前的平静期，等离子体层最初较大且向外延伸。随着磁暴主相内地磁活动增强，尤其是在晨侧和夜侧区域，等离子体层受到侵蚀，导致等离子体层顶向地球靠近。相反，等离子体层在午后区域变得延伸，并且在SYM‐H指数达到最低值前后出现了等离子体层羽流。在随后的恢复相期间，等离子体层羽流消失。由于电离层外流，等离子体层开始恢复，等离子体层顶逐渐向较高的 L壳移动。总之，DEN2D模型成功地捕捉到了磁暴不同阶段（至少在我们当前理解的水平上）等离子体层的动态演化；即平静期的等离子体层、等离子体层的侵蚀与重新填充，以及羽流的形成。

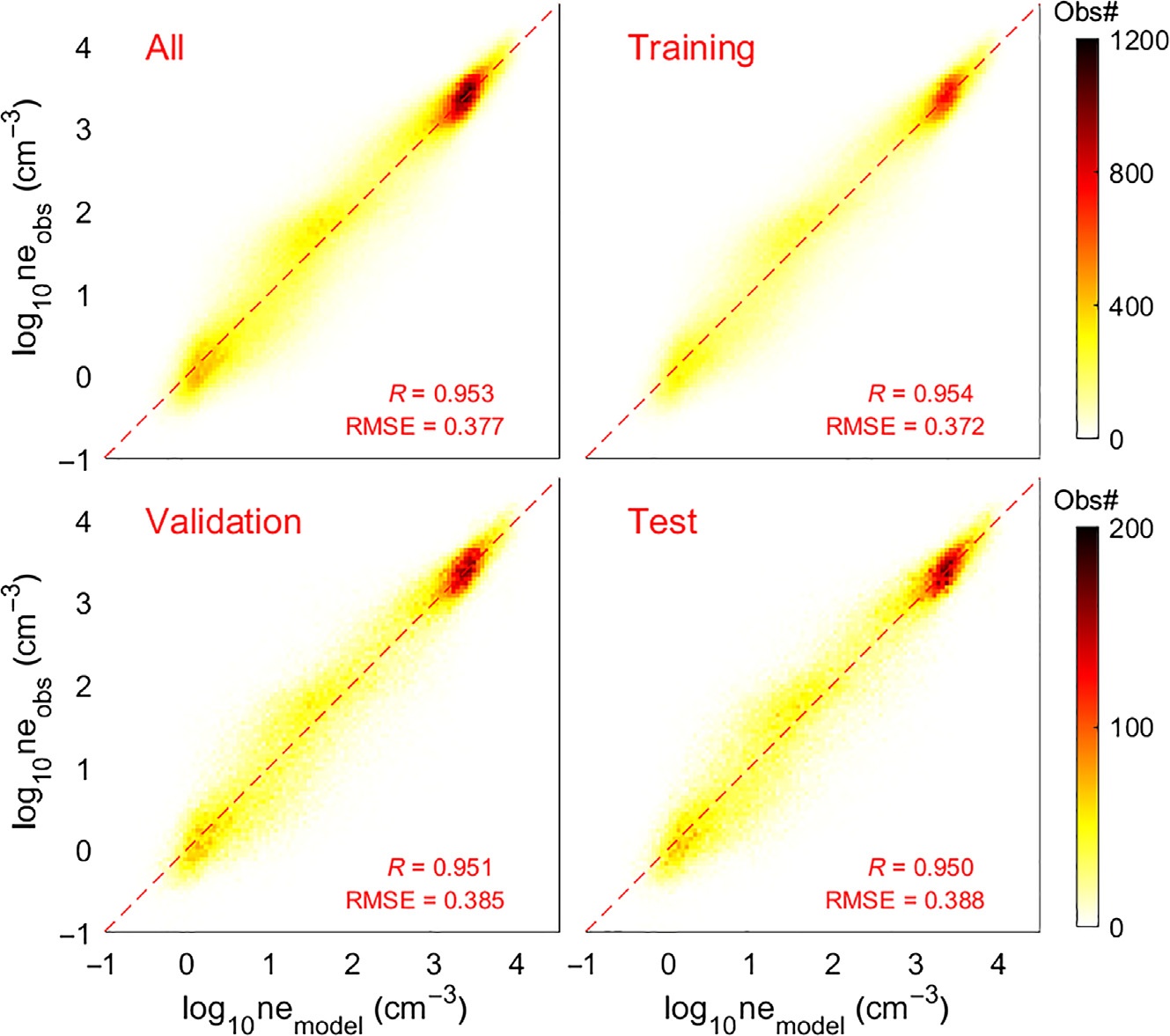
DEN2D模型的性能可以通过多个相关系数（r）和均方根误差（RMSE）来表示。图3 显示了整个数据集、训练集、验证集和测试数据集中模拟的（x轴）与观测的（y轴）密度之间的互相关系数，颜色表示每个区间内观测‐模型配对的数量。大多数观测‐模型配对集中在对角线（y= x）附近，表明大多数观测值可以被准确模拟。所有数据集的皮尔逊相关系数均大于且接近0.95，这意味着r2= ∼90.8%的观测到的变异性被捕捉到。由于测试数据集未参与训练过程，因此可用于评估DEN2D模型对样本外观测的预测能力。电子密度测试数据集上的均方根误差（log10 ne)为0.388，可转换为 100.388= 2.44倍因子。这表明DEN2D模型预测样本外观测值的误差约为2倍因子，非常接近从航天器电位获取电子密度方法本身固有的∼2误差因子（Li et al., 2010年）。该误差远小于典型密度变化在地磁暴（例如，图2g–l）的量级相差几个数量级。因此，人工神经网络预测效率的进一步提升变得不那么显著，因为模型受到观测误差的限制。

4 高级应用

我们在第3节中通过提出在扩展时间（和空间）内重建稀疏测量量Q的问题开始讨论，将其重构为仅在一个时间快照下覆盖扩展空间的该量的快照，并以二维电子数密度为例说明了人工神经网络技术的应用。现在我们回到使用相同技术复现任意量的一般问题，并简要探讨其一系列应用。首先，我们展示等离子体层密度DEN2D模型向三维的简单扩展，然后讨论哨声波和嘶嘶声波，最后深入探讨辐射带通量预测这一重要问题。

4.1 DEN3D模型

DEN2D模型可以很容易地扩展为研究三维（Chu 等人，2017a）等离子体层动力学，方法是将卫星的地磁纬度作为设计矩阵 X中的一个输入参数，并扩展卫星数据集，使其包含足够多的非赤道样本。三维动态电子密度（DEN3D）模型利用四颗卫星上搭载的波动仪器通过上混杂共振频率识别出的电子密度，这些卫星包括赤道卫星ISEE（Gurnett 等人，1978）和 CRRES（Anderson 等人，1992），以及极轨卫星POLAR（Gurnett 等人，1995）和 IMAGE（Reinisch 等人，2000）。DEN3D模型的架构和训练过程在Chu 等人（2017a）中有详细描述，采用5分钟平均值（类似于DEN2D模型），共获得217,500个数据点，覆盖所有 L壳至L ∼ 11、地磁纬度在 −50到50度之间以及所有地磁地方时。DEN3D模型对测试数据集的三维等离子体密度数据集变化预测的相关系数达到0.954，并能以约2倍因子的误差预测样本外观测结果。

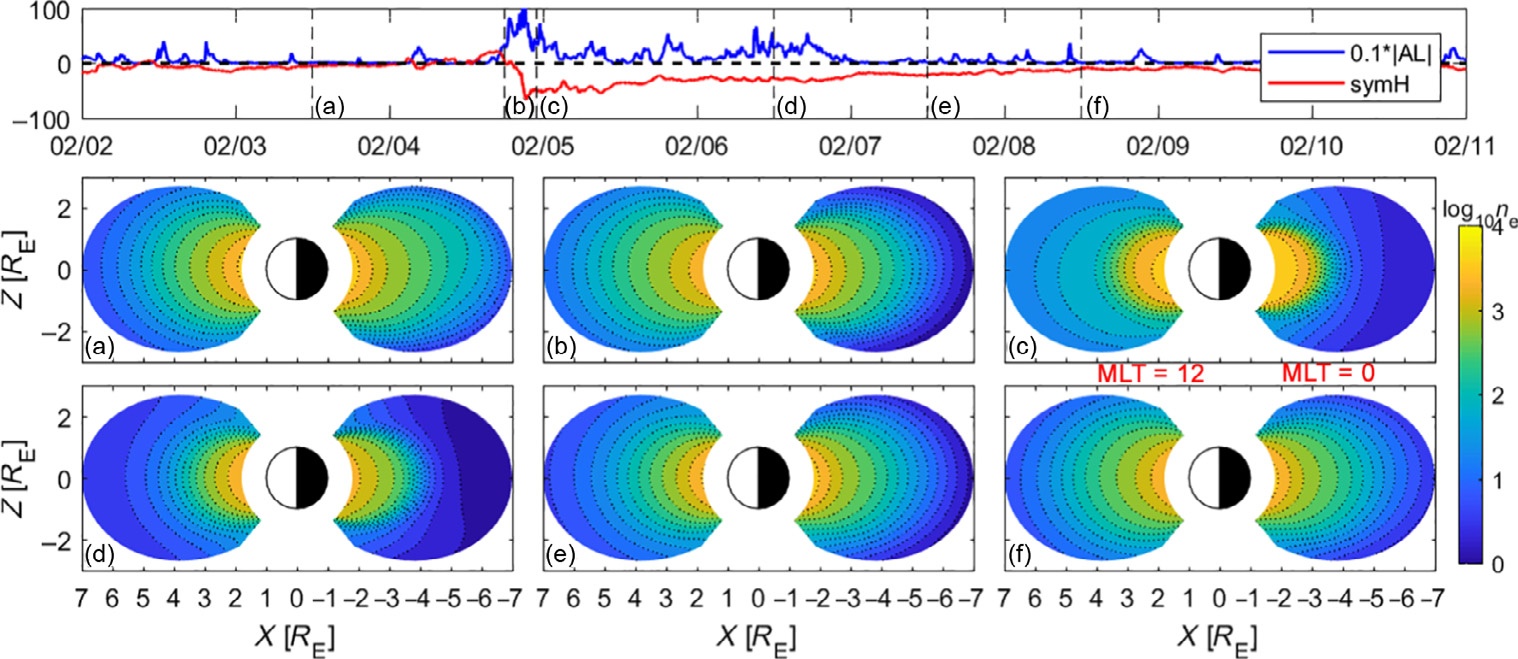
DEN3D模型已应用于2011年2月4日发生的同一风暴事件，以研究沿磁场线的电子密度变化。我们注意到数据集覆盖1977年至2005年，因此2011年事件完全属于样本外。例如，图4显示了在不同时间（由垂直虚线标示）正午‐子夜子午面内的电子密度剖面。在平静时期（图a），等离子体层较大且向外延伸。在主相开始时（图b），夜侧等离子体密度变得耗尽，随着等离子体层顶向地球收缩，这种耗尽进一步发展（图c）。另一方面，由于等离子体层羽流的形成，昼侧等离子体密度增加，等离子体层顶移动到更高的L壳（图c）。在恢复相期间，羽流消失，电子密度因电离层外流而开始增加，导致等离子体层顶缓慢向外移动（图d–f）。总之，DEN3D模型成功地在三维空间中重现了该风暴事件中的多种已知动态特征，如等离子体层侵蚀与恢复以及羽流的形成。

4.2 合声与嘶嘶声波模型

我们现在展示人工神经网络技术在内磁层波动环境中的应用，特别是用于重建两种已知在驱动辐射带粒子动力学中起关键作用的波，即哨声模合唱波和等离子体层嘶嘶声（Horne等人，2003；Thorne，2010年，以及其中的参考文献）。

设计矩阵和目标矩阵的构建方式与第3节中所示相同，但保留了卫星的纬度位置，以生成一个三维模型。对于哨声波，将低频段波磁场强度在0.1–0.5 fce（其中fce为赤道映射电子回旋频率）范围内进行积分，并降采样为5分钟平均强度值。数据来自两个任务：（1）范艾伦探测器A和探测器B上搭载的EMFISIS仪器（克莱齐格等人，2013年），时间范围为2012年10月1日至2014年7月1日；（2）THEMIS任务中探针A、D和E上搭载的搜索线圈磁力计仪器（勒孔特尔等人，2008年；鲁等人，2008年），以FFF模式采集，时间范围为2010年5月1日至2014年7月1日。最终的数据集包含∼372,000个值，采样区域从 ∼600km高度到L壳= 10（我们人为剔除了L壳>10的数据样本，因为我们的关注重点是L壳< 10的内磁层，但 THEMIS的绝大多数样本是在远地点或接近远地点处采集的，即L壳> 10）。由于哨声波通常与亚暴的关系比与磁暴更密切，因此我们选择使用AE指数作为预测因子（而非常用的 SYM‐H），并采用前5小时间隔内以5分钟采样间隔的数据。

我们训练的ANN合声模型的结果如图5所示，时间段为2012年3月10日，这是一个地磁活跃期。图5A显示了在我们的快照时刻02:15前后发生的一系列亚暴，而B–D面板展示了合声波作为L和磁地方时的函数，在三个地磁纬度值上的分布：分别为 λ= 0度（赤道）、λ= 15度（中纬度）和 λ= 30度（高纬度）。与以往研究一致，合声波在赤道附近的分布倾向于保持在等离子体层外的低密度区域，并在黎明扇区达到最大功率，且随着纬度升高，功率最大值随磁地方时增加并向更低的L壳移动（例如，Bortnik 等人，2007；Li 等人，2009；Meredith 等人，2003，2013）。该事件的动态模拟（未显示）表明，AE指数上升后不久，波功率往往增强并进入较低的L壳，这与地磁对合声波的控制一致。我们还构建了一个类似的高频段合唱波模型，其趋势是跟随低频段合声波的主要赤道功率分布，但在纬度上传播得不高，基本局限于 λ ∼ 10至15度范围内（未显示）。我们还注意到，图B中地球昏侧低L壳处的波功率很可能是泄漏到合声频率波段的甚低频发射器功率，但我们选择在模型中保留它，以说明人工神经网络模型能够捕捉来自多种源的波功率。

采用非常相似的方法，但使用2012年10月1日至2014年10月1日期间仅来自范艾伦探测器A和B卫星的数据，我们构建了一个模型利用SYM‐H指数过去10小时的值（这是等离子片电子从夜侧漂移到日侧并激发/放大嘶嘶声的合适时间尺度），以5分钟采样间隔对内磁层中的等离子体层嘶嘶声强度进行研究。生成的数据集包含 ∼290,000个样本，覆盖从 ∼600 km高度到L ∼ 6的所有磁地方时区域。图6 展示了我们的人工神经网络模型的结果，其中等离子体层嘶嘶声在与图5相同的暴期间（2012年3月10日）重建，处于一次强地磁暴的恢复相（最小Dst ∼ −150 nT）。与以往的研究一致，嘶嘶声被发现局限于等离子体层，并在昼侧达到最大强度，在较高纬度处强度更高（例如，Li等人，2015年；Meredith等人，2013年）。尽管尚未对这些初始的哨声和嘶嘶声模型进行优化，且数据样本数量相对较少，但互相关系数仍然合理，哨声和嘶嘶声分别为 ∼0.73 和 ∼0.62，误差因子为 ∼2（均方根误差 ∼ 0.3，两种情况均为如此）。

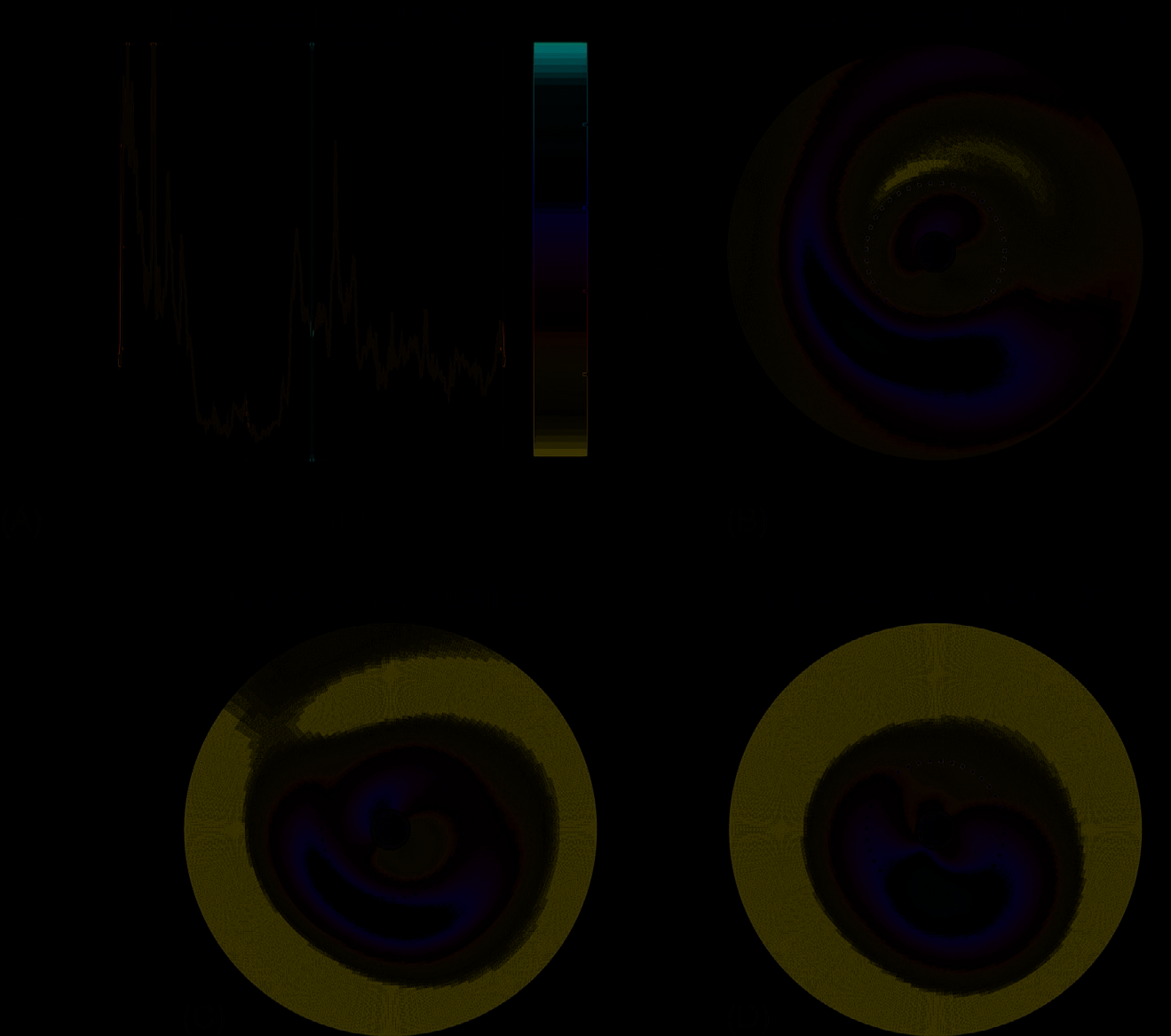
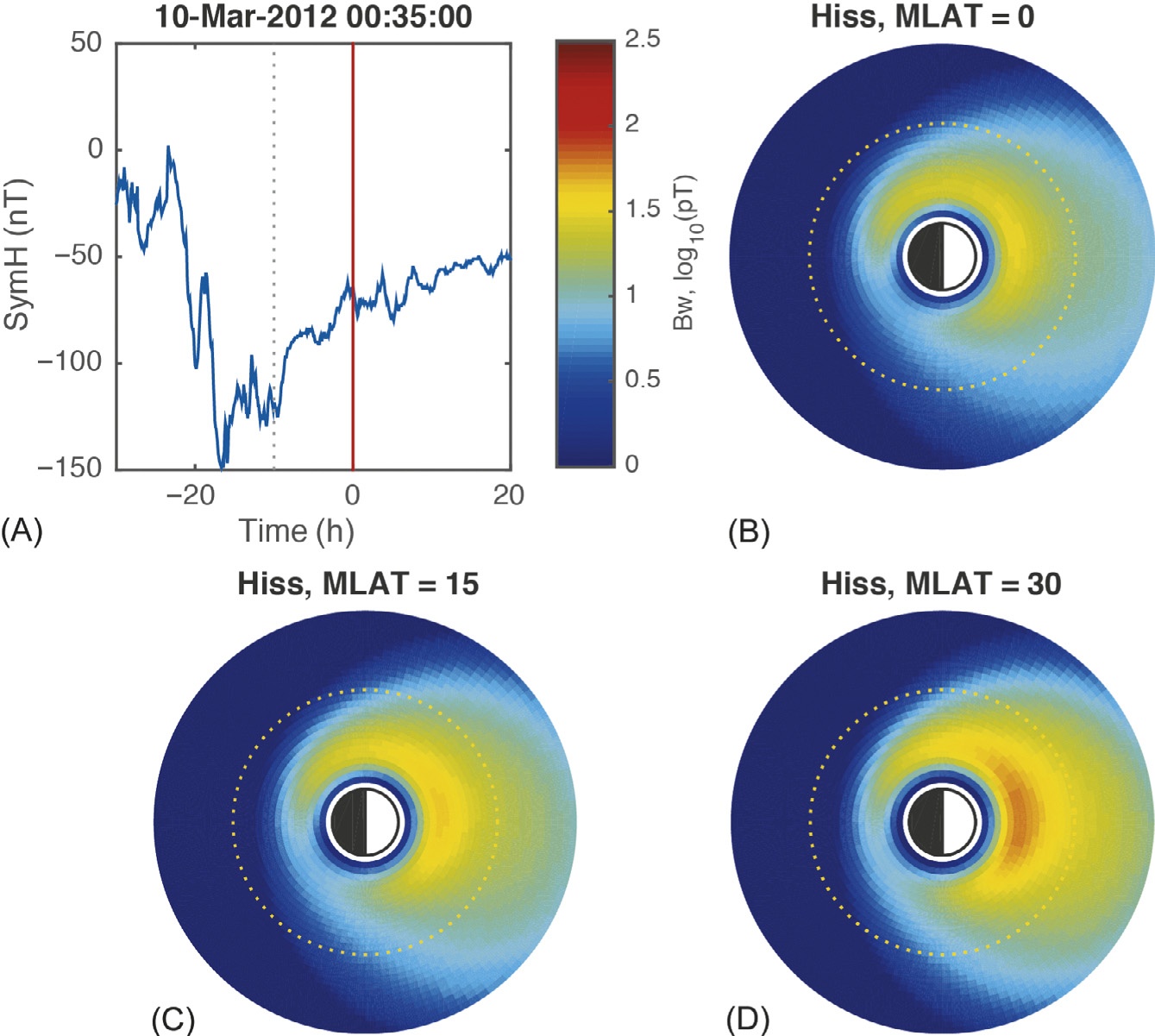
需要注意的是，图5 和 6都是以5分钟采样间隔生成的动态时空演化哨声波和嘶嘶声波序列快照中的单个快照。这类动态图像包含大量信息，既可用作研究哨声波/嘶嘶声波自身动力学特性的工具，也可将波的强度用于其他应用，例如辐射带通量的预测，我们接下来将讨论这一点。

4.3 辐射带通量建模

地球电子辐射带由被地球磁场捕获的高能电子（∼兆电子伏特）组成，包括两个区域：内带（L< 2.5）和外带（L> 3），两者之间被一个缝隙区隔开（Lyons 和 Thorne，1973年）。外带尤其具有高度可变性（Thorne，2010年），由于内部充电、单粒子翻转和总辐射剂量等原因，对外层空间中的各种航天器系统构成空间天气危害（例如，美国国家研究委员会，2013年；Cho 等人，2015年；Baker 和 Lanzerotti，2016年以及其中引用的大量参考文献）。预测和确定辐射带通量强度一直是空间天气研究人员的长期目标，本文将讨论实现这一目标的一些潜在策略。

我们首先将人工神经网络技术直接应用于范艾伦探测器A和B卫星上搭载的相对论性电子质子望远镜（Baker et al.，2012）测量的高能通量预测。此处使用的数据时间区间为2012年10月1日至2014年11月1日，涵盖E= 1.8 兆电子伏特至E= 7.7 兆电子伏特之间的八个能量通道，在L< 6处。作为回归变量，我们使用前10小时区间内以5分钟采样间隔采集的SYM‐H指数，共得到∼188,000个独立的数据样本。我们注意到，10小时是我们根据等离子体片电子从夜侧到日侧的漂移周期估算出的人工神经网络模型合适的时间尺度，但极端相对论性电子的加速可能需要更长的时间。模型与数据之间的典型互相关系数范围在∼0.73–0.84之间，通常随能量增加而逐渐降低。

我们的人工神经网络模型的一个示例如图7所示，其中重建了同一地磁暴时段（2012年3月10日）恢复相中的极端相对论性辐射带通量，该时段在图5和图6中已研究过。有几点需要注意：虽然1.8 兆电子伏特通量显示出某种程度上合理的内带和外带，并且其强度随SYM‐H指数变化，但随着电子能量的增加，行为变得越来越不真实。在E ∼5–6 兆电子伏特范围（G–H面板），人工神经网络模型突出了遇到高强度通量的单个卫星轨迹，这对于人工神经网络而言是“正确”的行为，因为它不了解控制高能电子漂移的基本物理。这种行为可以通 过进一步检查例如Baker et al.（2014）的图1来理解，该图显示在2012年9月1日至2014年5月1日的整个时段内，8.8 兆电子伏特通道中实际上只有1次增强事件，而在5–6 兆电子伏特范围内也只有少量事件。本质上，极端相对论性电子通量呈现出一种“数据匮乏”环境，这意味着诸如我们的人工神经网络模型之类的技术不应直接使用。

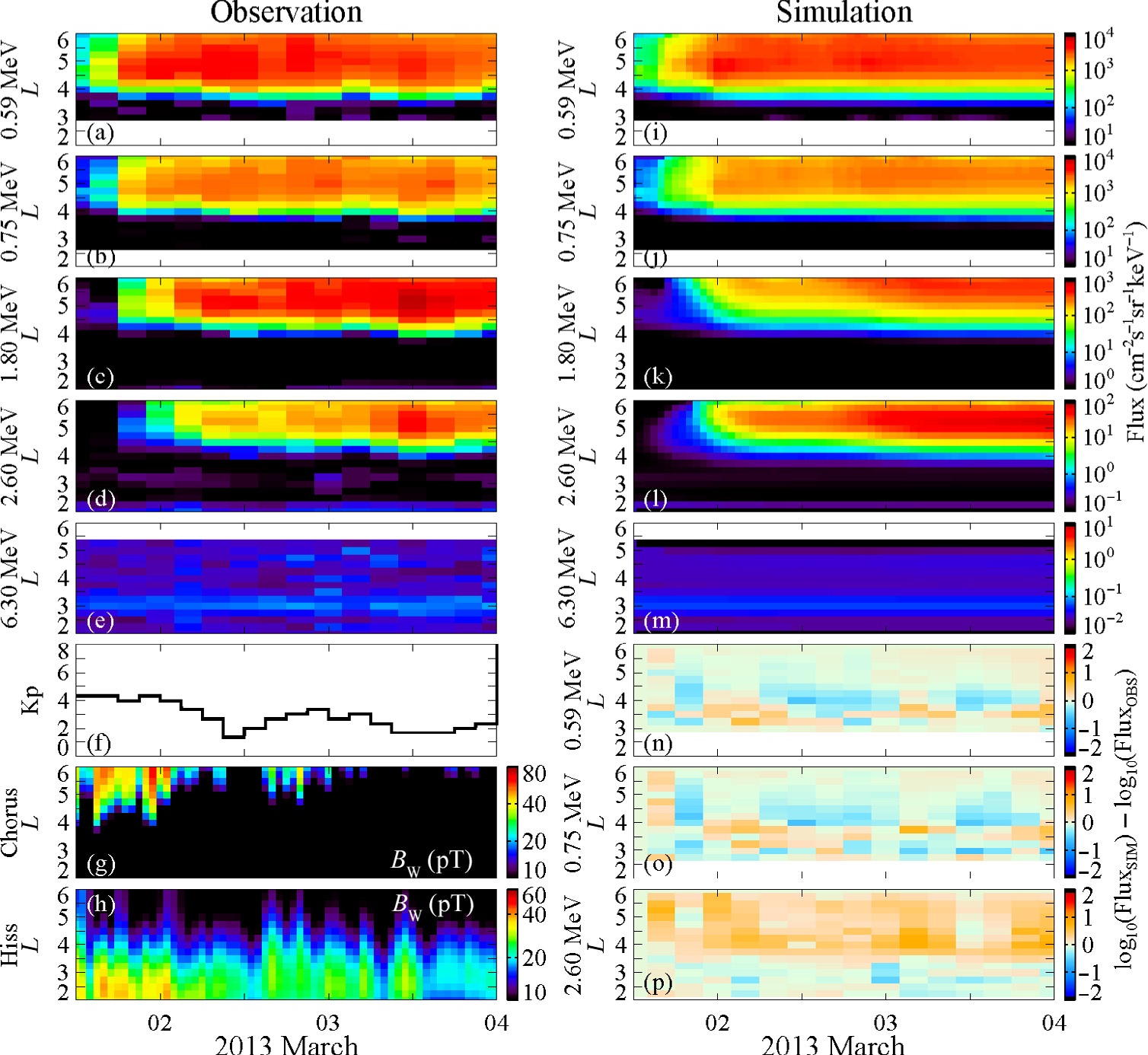
相反，我们建议采用一种方法，在“数据丰富”的环境中利用人工神经网络模型的优势，并借助基于物理的模型将这些信息进行投影到“数据匮乏”环境。这种方法的一个示例如图8所示，我们使用了福克‐普朗克扩散模型（Ma 等人，2015年），该模型由我们的基于人工神经网络的哨声和嘶嘶声模型（见图5 和 图6）以及总电子密度模型驱动，用于计算随时间变化的、弹跳和漂移平均扩散系数。径向扩散的影响通过经验拟合的方式引入，即对DLL与Kp指数及L壳的关系进行拟合，参见Ozeke 等人（2014）。

我们将该技术应用于2013年3月1日至4日发生的一次中等强度地磁暴（最小Dst ∼−55 nT），如图8所示。Reeves et al. （2016）详细报道了同一时期能量依赖性电子衰减及相应的辐射带结构。此次事件中的高能电子加速和衰减过程随后由Ma et al. （2016）利用基于物理的模型结合可用测量值输入进行了模拟。图8显示，尽管我们的模型以较为粗略的方式仅包含了少数几个物理过程，但结果相当真实，大致给出了所有能量下高能电子量化所需的时间尺度、量化发生的L壳正确范围，以及近似正确的最大通量强度和被量化的电子能量（例如，2.6兆电子伏特通量增强而6.3兆电子伏特通量未增强）。对于数百千电子伏特能量的电子通量演化，在误差较小的情况下基本得以重现，特别是在具有重要外带粒子群的L壳（L ≥ 4）上表现良好。模拟中2.6兆电子伏特电子通量被高估，但电磁离子回旋波的可能存在的影响可能导致2.6兆电子伏特电子进一步损失。能量依赖性的加速与衰减特征以及电磁离子回旋波的潜在作用，与利用可用卫星测量数据提供的等离子体波动输入进行的基于物理模型的模拟结果一致（Ma et al.，2016）。因此，我们认为人工神经网络建模技术不仅可作为独立模型使用，还可作为基于物理模型的输入模型，如图8所示。

5 总结与讨论

本章旨在解决的基本问题是，寻找一种方法来重构某个物理量Q的全局、随时间变化的分布，该物理量已在磁层内不同位置和不同时刻进行了稀疏采样。我们所采用的方法基于人工神经网络（ANN），在第2节中对此进行了简要回顾，然后通过电子数密度数据集进行示例说明，其中我们仅基于THEMIS数据构建了内磁层的二维（赤道面）模型，并仅使用5小时SYM‐H指数作为输入。令人惊讶的是，即使这个简单的模型也能够捕捉到等离子体层和等离子体槽的主要动力学行为，并对样本外数据解释了>90%的方差。

随后，我们展示了人工神经网络技术的更高级应用，首先将简单的二维模型扩展为完整的三维模型（DEN3D），然后通过建模哨声模合唱波和等离子体层嘶嘶声波，说明其在内磁层波动环境中的应用。最后，我们探讨了辐射带通量预测/确定的问题，并指出直接应用人工神经网络方法实际上并不适用于极端相对论性电子通量，因为这是一个数据匮乏环境。这一困难可以通过采用基于物理的福克‐普朗克扩散模型来克服，该模型由人工神经网络模型驱动，用于描述哨声波和嘶嘶声波；通过这种方式，我们将信息从数据丰富（波动）环境传递到数据匮乏（极端相对论性电子通量）环境。

图第4节中所示的波和粒子数据示例具有说明性，仅代表了一系列应用中的冰山一角。本章讨论的人工神经网络技术非常通用，可以设想在不久的将来，来自当前和以往的仪器与任务的大量存档数据都可以被类似地“学习”。例如，目前在空间物理数据设施、国家空间科学数据中心、协调数据分析网站等数据档案馆中存储了多太字节数据，由于这些仪器早已退役，无法用于研究当前正在发生的地磁事件，因此这些数据大部分仍未被使用。但如果能够基于人工神经网络技术开发出这些仪器的“虚拟”版本，以重现特定地磁驱动条件下某台仪器或数据集通常会产生结果，情况会如何？尽管每个虚拟重建的仪器单独来看都不完美，但拥有大量此类虚拟仪器将开启目前难以想象的探索领域，而利用现有的数据、计算资源和建模技术，这一目标完全可以实现。这样的虚拟空间环境可能是本文所讨论的人工神经网络技术的自然终点。

最后需要指出的是，统计预测技术（如人工神经网络模型）并非也不可能是物理建模/理解的替代品，尽管近期一些报告提出了这种建议（安德森，2008）。像人工神经网络这样的模型在密集采样的区域表现良好，但在进行外推时通常表现不佳（例如，图7）。而基于物理的模型，假设所有物理过程都已正确表示，则应能在其典型运行范围内实现良好的外推性能。作者认为，机器学习技术一个特别富有成效的应用在于所谓的“洞察发现”，即发现可能未被包含在基于物理的模型中的潜在重要物理过程，从而使得基于物理的建模能够用于预测和描述此前未遇到的情况。