数据结构和算法 二十一、贪心算法

1、贪心算法概述

        求解最优化问题的算法通常需要一系列的步骤，每个步骤面临很多选择。对于许多最优化问题，可以使用更简单、高效的算法。

        贪心算法（greedy algorithm）就是这样的算法，每一步都做出当时看起来最佳的选择。 贪心算法并不保证得到最优解。但是对于很多问题确实可以求得最优解。

为了达到最大和的目标，在每一步，贪心算法都会选择看起来是最优的直接选择，所以它会在第二步选择 12 而不是 3，并且不会达到包含 99 的最佳解决方案.

 

Dijkstra 算法，用于查找a和b之间的最短路径。它选择距离最短的未访问顶点，计算通过它到每个未访问邻居的距离，如果更小，则更新邻居的距离。与邻居完成后，标记已访问（设置为红色）。

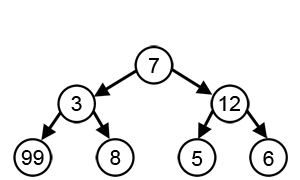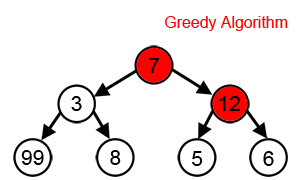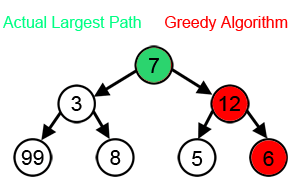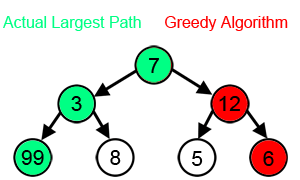
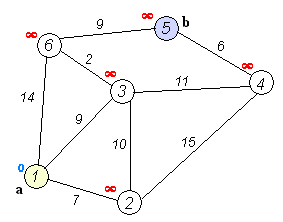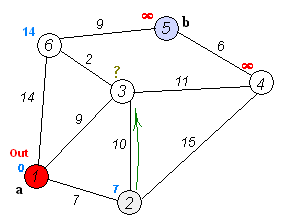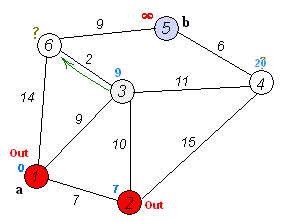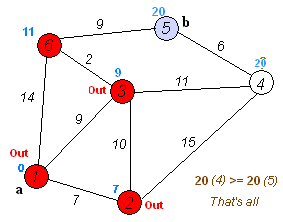
2、活动选择问题

        考虑以下 6 个活动按完成时间排序。

        开始[] = {1, 3, 0, 5, 8, 5}; 完成[] = {2, 4, 6, 7, 9, 9};

        一个人最多可以进行四项活动。 这可以执行的最大活动集是 {0, 1, 3, 4} (这些是 start[] 中的索引和结束[] )

        贪心的选择是总是选择剩余活动中完成时间最短且开始时间大于或等于先前选择的活动的完成时间的下一个活动。我们可以根据完成时间对活动进行排序，以便我们始终将下一个活动视为最短完成时间的活动。

        1) 根据完成时间对活动进行排序。

        2) 从排序后的数组中选择第一个活动并打印。

        3) 对排序数组中的剩余活动执行以下操作。 

#include <bits/stdc++.h>
using namespace std;

// 打印最多可以由一个人完成的活动，一次一个。
// n --> 活动数量
// s[] --> 包含所有活动开始时间的数组
// f[] --> 包含所有活动完成时间的数组
void printMaxActivities(int s[], int f[], int n)
{
	int i, j;

	cout <<"Following activities are selected "<< endl;

	// The first activity always gets selected
	i = 0;
	cout <<" "<< i;

	// Consider rest of the activities
	for (j = 1; j < n; j++)
	{
	    // 如果此活动的开始时间大于或等于之前选择的活动的结束时间，则选择它
	    if (s[j] >= f[i])
	    {
		    cout <<" " << j;
		    i = j;
	    }
	}
}

int main()
{
	int s[] = {1, 3, 0, 5, 8, 5};
	int f[] = {2, 4, 6, 7, 9, 9};
	int n = sizeof(s)/sizeof(s[0]);
	printMaxActivities(s, f, n);
	return 0;
}

3、Kruskal最小生成树

        给定一个连通无向图，该图的生成树是一个子图，它是一棵树，将所有顶点连接在一起。一个图可以有许多不同的生成树。加权、连通、无向图的最小生成树 (MST)或最小权重生成树是权重小于或等于所有其他生成树的权重的生成树。

        算法步骤

        1、按权重的递增顺序对所有边进行排序。 

        2、选择最小的边。检查它是否与到目前为止形成的生成树形成一个循环。如果没有形成循环，则包括该边。否则，丢弃它。 

        3、重复步骤#2，直到生成树中有 (V-1) 条边。

#include <bits/stdc++.h>
using namespace std;


class DSU {
	int* parent;
	int* rank;

public:
	DSU(int n)
	{
		parent = new int[n];
		rank = new int[n];

		for (int i = 0; i < n; i++) {
			parent[i] = -1;
			rank[i] = 1;
		}
	}

	// 查找方法
	int find(int i)
	{
		if (parent[i] == -1)
			return i;

		return parent[i] = find(parent[i]);
	}
	// union方法
	void unite(int x, int y)
	{
		int s1 = find(x);
		int s2 = find(y);

		if (s1 != s2) {
			if (rank[s1] < rank[s2]) {
				parent[s1] = s2;
				rank[s2] += rank[s1];
			}
			else {
				parent[s2] = s1;
				rank[s1] += rank[s2];
			}
		}
	}
};

class Graph {
	vector<vector<int> > edgelist;
	int V;

public:
	Graph(int V) { this->V = V; }

	void addEdge(int x, int y, int w)
	{
		edgelist.push_back({ w, x, y });
	}

	void kruskals_mst()
	{
		// 1. 排序所有边
		sort(edgelist.begin(), edgelist.end());

		// 初始化
		DSU s(V);
		int ans = 0;
		cout << "Following are the edges in the "
				"constructed MST"
			<< endl;
		for (auto edge : edgelist) {
			int w = edge[0];
			int x = edge[1];
			int y = edge[2];

			// 如果它确实形成一个循环，则在 MST 中占据优势
			if (s.find(x) != s.find(y)) {
				s.unite(x, y);
				ans += w;
				cout << x << " -- " << y << " == " << w
					<< endl;
			}
		}
		cout << "Minimum Cost Spanning Tree: " << ans;
	}
};

int main()
{
	/* 创建一个如下的图
				10
			0--------1
			| \	 |
			6| 5\ |15
			|	 \ |
			2--------3
				4	 */
	Graph g(4);
	g.addEdge(0, 1, 10);
	g.addEdge(1, 3, 15);
	g.addEdge(2, 3, 4);
	g.addEdge(2, 0, 6);
	g.addEdge(0, 3, 5);

	g.kruskals_mst();
	return 0;
}