机器学习笔记 - 支持向量机(SVM)背后的数学一

一、支持向量机概述

        SVM 是一种监督学习模型，就是说需要一个已标记的数据集。

        SVM学习到了什么？它学习一个线性模型。什么是线性模型？对简单的平面来说：它是一条线（复杂的话它是一个超平面）。如果您的数据非常简单并且只有两个维度，那么 SVM 将学习一条能够分离数据的线。

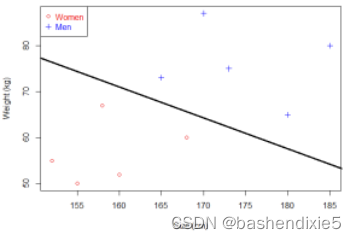
        如果只是学一条线。就不会需要线性模型了，所以大概是以下流程：

        1）我们假设我们要分类的数据可以用一条线隔开

        2）我们知道一条线可以用等式表示是（这就是平面条件下的模型）

        3) 我们