算法通关村—如何使用中序和后序来恢复一颗二叉树

二叉树

基本概念

1. 节点的度：一个节点含有的子节点的个数称为该节点的度
2. 树的度：一棵树中，最大的节点的度称为树的度，注意与节点度的区别；
3. 叶节点或终端节点：度为O的节点称为叶节点：
4. 非终端节点或分支节点：度不为0的节点：
5. 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点：
6. 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点：
7. 兄弟节点：具有相同父节点的节点互称为兄弟节点：
8. 节点的祖先：从根到该节点所经分支上的所有节点
9. 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
10. 森林：由m(m>=0)棵互不相交的树的集合称为森林：
11. 无序树树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树：
12. 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树：
13. 二叉树：每个节点最多含有两个子树的树称为二叉树
14. 从根节点到看叶节点（从顶看底）是深度，从叶节点看根节点（从底看顶）是高度

请注意，我们通常将「高度」和「深度」定义为「走过边的数量」，但有些题目或教材可能会将其定义为「走过节点的数量」。在这种情况下，高度和深度都需要加 1 。

树的遍历方式

树的遍历有两种：

• 深度优先遍历: 先往深走，遇到叶子节点再往回走。
• 广度优先遍历: 一层一层的去遍历，一层访问完再访问下一层。

深度优先又有前中后序三种，而且这个前是相对于中间父节点来说的
看如下中间节点的顺序，就可以发现，访问中间节点的顺序就是所谓的遍历方式

前序遍历: 中左右
中序遍历: 左中右
后序遍历: 左右中

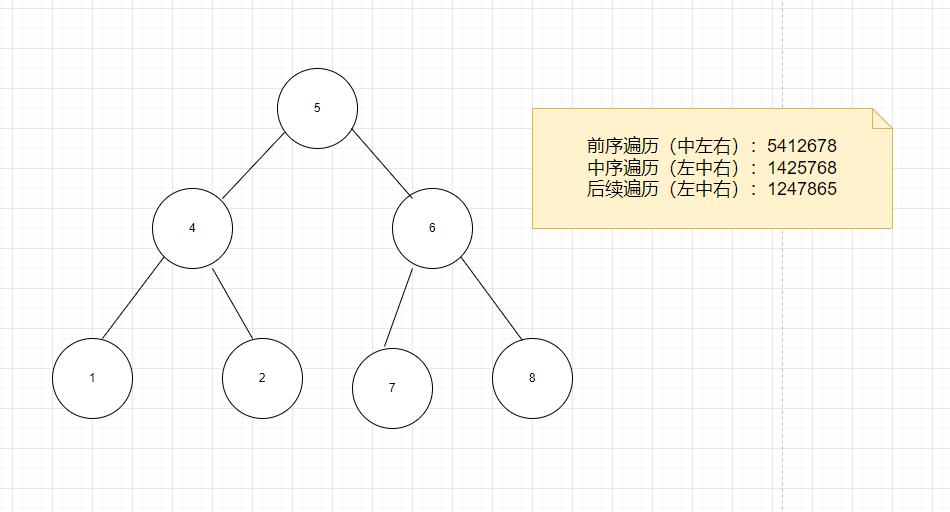
使用中序和后序来恢复一颗二叉树

看三个序列排序后的结果

1. 前序排序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
2. 中序排序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
3. 后序拍戏：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

目的是把 ta 恢复成二叉树

我们从后序结果中就可以得知 中间父节点是 1
所以我们的中序可以分为以下三个部分

[3 4 8 6 7 5 2 ] 1 [ 10 9 11 15 13 14 12]

同时后序节点也可以分为

[8 7 6 5 4 3 2 10 15 14 13 12 11 9] 1

中间父节点左边是左子树，右边是右子树

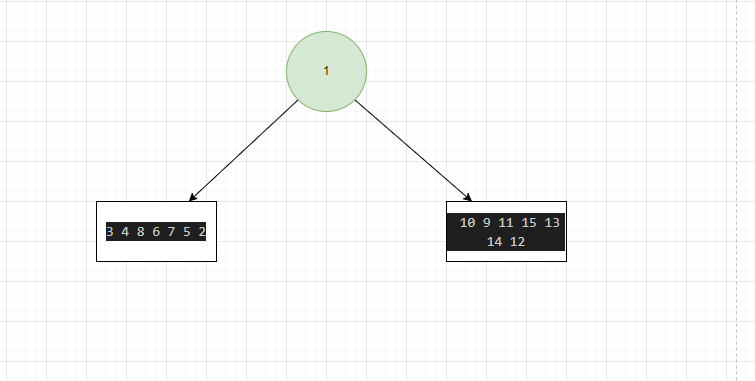
我们接着往下找，我从前中后对应的实例图示发现（第一张图片），发现 9 依然是一个节点

我们可以把 后续节点 和 中序节点分别进行分割

• 后续节点：[8 7 6 5 4 3 2 10 15 14 13 12 11] 9
• 中序节点：[10] 9 [11 15 13 14 12]

于是二叉树就变成了这样

继续

我们们把 后续节点 和 中序接再进行分割

• 后续节点：[8 7 6 5 4 3 2 10 15 14 13 12] 11
• 中序节点： 11 [15 13 14 12]

继续分割

• 后续节点：[8 7 6 5 4 3 2 10 15 14 13 ] 12
• 中序节点： [15 13 14 ] 12

最终变成

另一侧同理

最终去掉 null 得到