图-最短路径-Dijkstra算法

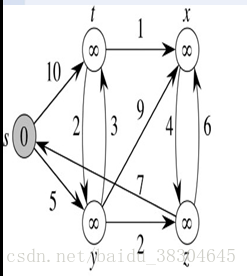
假若要在计算机上建立一个交通咨询系统则可以用图的结构来表示实际的交通网络。图中顶点表示城市，边表示城市间的交通联系。从A城到B城,旅客更关心节省交通费用，司机则对里程与速度更感兴趣。可以对边赋以权，权的值表示两城市间的距离，或途中所需时间。我们需要求出最短路径，即权值最小的路径。

首先介绍一种从某个源点到其余各顶点的最短路径的算法：Dijkstra算法。

输入：创建图。（此处设s为源点）

输出：源点到其他点的最短距离以及路径。

运行结果：

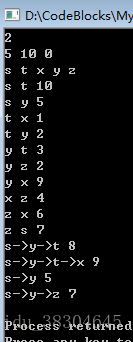
算法思想：

1、设置集合S存放已经找到最短路的点的集合。

2、将源点并入S，初始化源到V-S中各点的当前最短路径。

3、在V-S中找当前路径最短的顶点并入S，每并入一个新顶点都要据此更新源到其他点的距离。

重复步骤三，找最短路并更新，共重复n-1轮。

实现：

设辅助数组D，D[k]存储源到顶点k的当前最短路长度

final[k]标记k号顶点是否并入S

p[v]记录源到v的当前最短路径。

算法复杂度：O(G.vernum^2)

邻接矩阵存储：

typedef char   PathArray[50];
typedef int    DistancArray[MVNUM];

void ShortestPath_DIJ(MGraph G,int v0,PathArray P[MVNUM],DistancArray &D){
    /*用Dijkstra算法求有向网的v0顶点到其余顶点v的最短路径P[v]及其带权长度D[v]
    设置一集合S存放已经找到最短路的点的集合，将源点并入S，初始化V-S各点的当
    前最短路径 重复以下步骤n-1次 在V-S中找当前路径最短的顶点，并入S，据此更
    新源到其他点的距离
    final[v]为TRUE当且v属于S 即已经求得v0到v的最短路径 D[k]存储到顶点k的当
    前最短路距离 P[v]记录源到v的当前最短路径*/
    bool final[MVNUM];
    int v,w,i,min;
    char s[5],s1[4],s2[50];
    //初始化 并入源点并更新
    final[v0]=TRUE;
    D[v0]=0;
    for(v=0;v<G.vexnum;v++){
        if(v!=v0){
	    final[v]=FALSE;
	    D[v]=G.arcs[v0][v].adj;
            if(D[v]<INFINITY){
                s[0]=G.vexs[v0];
	        s[1]='-';
                s[2]='>';
                s[3]=G.vexs[v];
	        s[4]='\0';
  		strcpy(P[v],s);
	    }
	 }
    }
    for(i=0;i<G.vexnum-1;i++){
        //找当前路径最短的顶点 
        min=INFINITY;
        v=i;
        for(w=0;w<G.vexnum;w++)
            if(!final[w]&&min>D[w]){
                min=D[w];
	        v=w;
            }
        final[v]=TRUE;
	for(w=0;w<G.vexnum;w++){
            if(!final[w]&&(min+G.arcs[v][w].adj<D[w])){
	         D[w]=min+G.arcs[v][w].adj;
	         s1[0]='-';
                 s1[1]='>';
	         s1[2]=G.vexs[w];
		 s1[3]='\0';
		 strcpy(s2,P[v]);
		 strcpy(P[w],strcat(s2,s1)); //strcat 会改变左参数的值
	    }
	}
    }
    for(i=1;i<G.vexnum;i++)
        printf("%s %d\n",P[i],D[i]);
}

邻接表存储：

void ShortestPath_DIJ(ALGraph G,int v0,PathArray P[MVNUM],DistancArray &D){
    /*用Dijkstra算法求有向网的v0顶点到其余顶点v的最短路径P[v]及其带权长度D[v]
    设置一集合S存放已经找到最短路的点的集合，将源点并入S，初始化V-S各点的当
    前最短路径 重复以下步骤n-1次 在V-S中找当前路径最短的顶点，并入S，据此更
    新源到其他点的距离
    final[v]为TRUE当且v属于S 即已经求得v0到v的最短路径 D[k]存储到顶点k的当
    前最短路距离 P[v]记录源到v的当前最短路径*/
    bool final[MVNUM];
    int v,w,i,min,k;
    char s[5],s1[4],s2[50];
    ArcNode *p;
    //初始化 并入源点并更新
    final[v0]=TRUE;
    D[v0]=0;
    for(v=0;v<G.vexnum;v++){
        if(v!=v0)
        {
            D[v]=INFINITY;
            final[v]=FALSE;
        }
    }
    for(p=G.vertices[v0].firstarc;p!=NULL;p=p->nextarc){
        k=p->adjvex;
        D[k]=p->adj;
	s[0]=G.vertices[v0].data;
	s[1]='-';
        s[2]='>';
        s[3]=G.vertices[k].data;
	s[4]='\0';
	strcpy(P[k],s); 
    }
    for(i=1;i<G.vexnum;i++){
        //找当前路径最短的顶点
	min=INFINITY;
	v=i;
	for(w=0;w<G.vexnum;w++){
            if(!final[w]&&min>D[w]) {
	        min=D[w];
	        v=w;
	    }
	}
	final[v]=TRUE;
	for(p=G.vertices[v].firstarc;p!=NULL;p=p->nextarc){
	    k=p->adjvex;
	    if(!final[k]&&(min+p->adj)<D[k]){
		D[k]=min+p->adj;
		s1[0]='-';
                s1[1]='>';
		s1[2]=G.vertices[k].data;
		s1[3]='\0';
		strcpy(s2,P[v]);
		strcpy(P[k],strcat(s2,s1));
	    }
	}
    }
    for(i=1;i<G.vexnum;i++)
	printf("%s %d\n",P[i],D[i]);
}