混合交通中自动驾驶控制综述

最新推荐文章于 2025-12-12 20:30:00 发布

原创最新推荐文章于 2025-12-12 20:30:00 发布 · 826 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#自动驾驶 # 混合交通 # 人工智能 # 强化学习 # 博弈论

混合自主性时代的自动驾驶车辆控制综述：从基于物理的到人工智能引导的驾驶策略学习

摘要

本文旨在介绍和概述从人工智能（AI）领域中可能对混合自主时代自动驾驶车辆（AV）控制具有应用价值的模型与方法，特别是在自动驾驶车辆与人工驾驶车辆（HV）共同行驶的交通环境中。
这是首篇全面回顾交通工程与人工智能领域在混合交通建模方面文献的综述论文。我们将讨论人工智能引导的方法的最新进展，识别其中的机遇与挑战，并提出若干开放性问题。我们将自动驾驶汽车部署阶段划分为四个阶段：纯人工驾驶车辆阶段、人工驾驶车辆主导阶段、自动驾驶车辆主导阶段以及纯自动驾驶车辆阶段。本文主要关注后三个阶段。文中总结了各阶段所采用的模型，涵盖博弈论、深度（强化）学习以及模仿学习。在回顾相关方法时，我们重点关注以下研究问题：（1）在包含人类驾驶员和不可控自动驾驶车辆的混合交通中，应如何制定可扩展的驾驶策略以控制大量自动驾驶车辆？（2）如何估计人类驾驶员行为？（3）在环境中应如何建模不可控自动驾驶车辆的驾驶行为？（4）人类驾驶员与自动驾驶车辆之间的交互如何表征？此外，我们还提供了一系列与自动驾驶车辆相关的公开数据集和仿真软件。希望本文不仅能激励交通领域研究人员重新思考在数据短缺时代所建立的传统模型，还能促进与其他学科（特别是机器人学和机器学习）展开对话，携手共建安全高效的混合交通生态系统。

1. 引言

我们正得益于无处不在的传感器（如全球定位系统（Di¨等人，2017；Liao等人，2018；Shou和Di，2018；Meinrenken等人， 2020）、蓝牙（Allstrom等人，2014）和智能手机（Herrera等人，2010；寿等人，2020a）的普及，从数据短缺时代过渡到大数据时代。配备摄像头和激光雷达等传感器的自动驾驶车辆（AV）或5级自动驾驶汽车，有望提供激增的交通数据量（SAS，2015）。
随着从数据稀疏时代向数据丰富时代的转变，我们交通领域迫切需要一种方法论范式的转变，即从基于物理的模型转向人工智能（ AI）引导的方法，以预测由自动驾驶车辆与人工驾驶车辆共存所构成的未来交通动态
*通讯作者地址：美国哥伦比亚大学土木工程与工程力学系。电子邮件地址：sharon.di@columbia.edu(X.迪)。
目录列表请见ScienceDirect交通运输研
究C部分期刊主页：
www.elsevier.com/locate/trc
https://doi.org/10.1016/j.trc.2021.1030082020年7月8日收到；2020年12月25日修订后收到；2021年2月 1日接受
本文档由funstory.ai的开源PDF翻译库BabelDOCv0.5.10(http://yadt.io)翻译，本仓库正在积极的建设当中，欢迎star和关注。

1.1. 建模复杂性

迄今为止，大多数现有研究——或许并不意外——集中在两种极端情景上：一种是单个自动驾驶车辆在由大量人类驾驶员构成的生态系统中行驶，另一种是自动驾驶汽车车队在高速公路上行驶，且与人工控制的对应车辆几乎无交互。而对于更为现实却更具挑战性的过渡路径，关注则少得多。
示意图0

我们将自动驾驶汽车部署阶段划分为四个阶段：纯人工驾驶车辆、人工驾驶车辆主导、自动驾驶车辆主导和纯自动驾驶车辆。本论文重点关注后三个阶段。图1展示了每个阶段的建模复杂性。其中，对人工驾驶车辆主导和自动驾驶车辆主导阶段的建模最具挑战性，即混合自主。由于不同类型车辆之间存在未知且复杂的交互，这一阶段目前研究不足。我们进一步根据自动驾驶车辆与人工驾驶车辆的相对比例，通过以下概念对混合自主进行划分（如图1)中的红色框所示：
- 1自动驾驶车辆+ 1人类驾驶车辆：一辆自动驾驶车辆与一辆人类驾驶车辆交互；
- 1自动驾驶车辆+m人工驾驶车辆：一辆自动驾驶车辆在以人工驾驶车辆为主的交通环境中行驶；
- n辆自动驾驶车辆和m辆人工驾驶车辆：多辆自动驾驶汽车在以人工驾驶车辆为主的交通环境中行驶；
- n辆自动驾驶车辆与1辆人工驾驶车辆：多辆自动驾驶车辆在自动驾驶车辆主导的交通环境中与一辆人工驾驶车辆交互；它是n辆自动驾驶车辆与m辆人工驾驶车辆的一种特殊情况。
- n辆自动驾驶车辆：纯自动驾驶汽车市场，其中所有车辆都被自动驾驶车辆取代。因此，自动驾驶车辆之间相互作用。

备注1.1。 在撰写本论文的过程中，我们发现了另一篇关于自动驾驶车辆纵向控制及其对交通拥堵影响的综述论文（周和拉瓦尔， 2019）。主要区别在于，周和拉瓦尔（2019）专注于在空旷高速公路或仅有少数人工驾驶车辆环绕的情况下训练单个自动驾驶车辆（对应于1辆自动驾驶车辆+ m辆人工驾驶车辆），而本文回顾了混合自主环境下的更广泛文献。
在图1中，每个阶段相关的社区被绿色虚线框包围。交通领域主要关注纯人工驾驶车辆、自动驾驶车辆主导以及纯自动驾驶车辆的建模，而人工智能与控制领域则更关注人工驾驶车辆主导阶段，即单个自动驾驶车辆或有限数量的自动驾驶车辆在交通环境中行驶的情况。我们还在图的上部标明了关于自动化等级和车辆互联互通的建模假设。人工智能领域为人工驾驶车辆主导阶段开发的模型通常假设为4级或5级自动化且无联网，而为自动驾驶车辆主导和纯自动驾驶车辆阶段开发的模型，以及人工驾驶车辆主导阶段中的特定车队编队场景，通常采用1级或2级自动化并具备联网能力。接下来我们将进一步阐述这些社区在自主控制建模方面的差异。

1.2 学术界的分歧

交通领域和机器人学界的研究人员使用不同的术语来指代相同的量（费尔南德斯·菲萨克，2019）。本文在表1中列出了这两个社区的所有相关术语。
在自动驾驶控制器设计方面，这两个领域采取了两种不同的路径。首先，这两个领域的目标不同。交通研究人员旨在理解自动驾驶车辆对交通系统性能（从系统角度）的影响，例如交通拥堵（周和拉瓦尔，2019），而机器人学研究人员则主要关注为自动驾驶车辆开发最优驾驶策略，使其能够在随机环境中学习和适应（从车辆角度）。因此，这些领域在不同尺度上研究问题。
机器人学界旨在设计具有人在回路的自动驾驶车辆控制器。特别是，人‐信息‐物理系统领域的研究人员设计能够通过相互交互主动影响人类驾驶员的自动驾驶车辆，以实现高效驾驶。然而，其对系统级性能的影响仍不明确。交通系统领域则致力于理解自动驾驶车辆对交通系统性能的影响，包括出行时间、交通延误、交通安全和排放。由于多类别微观模型难以适应混合车辆类型的动态拓扑结构，研究人员更倾向于在宏观尺度上采用多类别方法对混合交通进行建模（塔勒布普尔和马赫马萨尼，2016；莱文和博伊尔斯， 2016；梅尔森等，2018年；陈等，2016；陈等，2017；科克尔曼，2017）。在道路网络中，研究主要集中在静态（陈等，2016；陈等，2017）或动态（德雷斯纳和斯通，2007；莱文和博伊尔斯，2015；莱文和博伊尔斯，2016；帕特尔等，2016；梅尔森等，2018 年）

表1 跨领域的术语（部分改编自Fernandez Fisac(2019)）。

交通	控制	AI	博弈论	交通	系统	环境	Game
交通演化	动态	转换	动态	交通状态	状态空间	状态	状态
CAV	CACC	AV	AV	车辆‐驾驶员单元	控制器	智能体	玩家
车辆控制	控制	动作	Play	车辆控制	控制	动作	Play
车辆控制律	控制律	策略	战略	车辆控制目标	Cost	奖励	收益
跟车	纵向控制	–		变道	横向控制	–
驾驶行为	驾驶员模型	驾驶员意图	理性	交通结果	最优控制	最优策略	均衡

交通分配模型被开发用于捕捉自动驾驶车辆的交叉口协调和路径选择行为。这些在宏观尺度上的模型可能缺乏对不同类型车辆在微观尺度上如何交互的详细解释。
其次，由于目标不同，人们采用了不同的自动驾驶车辆决策框架。学术研究人员不得不在模型或仿真中对自动驾驶车辆组件做出各种假设，因为现实世界中的自动驾驶汽车主要由私营公司开发和测试，而这些公司不愿意透露当前在公共道路上测试的自动驾驶车辆车队实际是如何编程来驾驶以及与其他道路使用者进行交互的。因此，不同的驾驶模型导致了不同的驾驶行为和交通模式。
交通和控制领域的研究通常将自动驾驶车辆（AV）视为遵循基于物理的模型的粒子或流体，这些模型包括最初为人类驾驶员开发的微观和宏观交通模型，并将自动驾驶车辆的行为设计为与人类驾驶车辆（HV）类似，只是自动驾驶车辆作为本质上的人类驾驶员能够反应更快、 “看得更远”以及“更了解”道路环境。例如，大多数研究将自动驾驶车辆等同于高级驾驶辅助系统（ADAS）或商用半自动驾驶功能（例如特斯拉’的Autopilot）。因此，这些系统的动态响应模型被用作自动驾驶车辆的驾驶模型（Naus等，2010；秦和Orosz，2013；Shladover 等，2015；Delis等，2016；周等，2020）。否则，自动驾驶车辆被视为具有修改参数的人类驾驶员（Schakel等，2010；Naus等， 2010；Ploeg等，2011；Milan´es等人，2014；Milan´es和Shladover，2014；金和Orosz，2014）。此外，由于这些自动驾驶系统仅在指定交通场景（如车队编组）中启用，因此控制模型也仅限于这些场景，无法适用于通用交通环境。
机器人学界则将自动驾驶车辆视为人工智能机器人或智能体，能够持续探索环境并利用最优动作（Sadigh等，2016b；刘和 Tomizuka，2016）。当环境可观测时，自动驾驶车辆根据预定义奖励函数在合作或非合作博弈中选择最优策略。强化学习作为一种前沿的学习范式，最初为机器人最优控制而开发，现已自然地应用于自动驾驶车辆。在此框架中，人类驾驶员被建模为自动驾驶车辆所处并进行移动和探索的环境的一部分，该过程采用马尔可夫决策过程（Mukadam等，2017）或模拟的无模型环境（吴等人， 2017b；吴等人，2017d；吴等，2017a；吴等人，2018；Kreidieh等，2018b）实现。
上述建模差异源于对车辆自动化等级的根本性不同假设。交通与控制学界主要关注1级或2级自动化（国际标准J3016，2016），并且通常结合车载联网功能。最受关注的场景是高速公路协同编队行驶，其中联网和自动驾驶车辆（CAVs）以车队形式行驶，以优化某些系统性能指标。相比之下，机器人学与人工智能社区主要关注5级自动驾驶车辆，这些车辆大多不依赖与邻近车辆的通信，运行于各种通用交通场景中，例如车道保持、变道、汇入和交叉通行。这种跨社区的差异源于两者对可行技术路径的截然不同信念：前者采取从1级到2级逐步、渐进的自动化进程，并通过车联网技术增强自动化水平，这一路径持续受到美国交通部（USDOT）推动；而以Waymo有限责任公司为代表的自动驾驶技术公司则选择从0级直接跃迁至完全自主驾驶，且不依赖任何通信基础设施。

备注1.2。 需要指出的是，自动化和联网是两种不同的技术。自动驾驶车辆可能具备也可能不具备联网功能，而联网车辆可能具备也可能不具备自动化功能。联网车辆指的是能够在地面交通生态系统中实现用户之间相互通信的车辆技术（美国交通部,2019年）。车对车（V2V）（或通信领域所使用的车载自组织网络（VANETs））和车对基础设施（V2I）通信是最受关注的研究场景。其使能机制包括专用短程通信（DSRC）和如5G的蜂窝通信。DSRC基础设施主要由美国交通部在试点测试平台上建立（美国交通部,2020年），而非大规模实际应用；而蜂窝网络则主要由私营公司部署。现有的自适应巡航控制系统（ACC）（即1级）不具备通信能力，但已有大量研究聚焦于具备通信功能的ACC，即协同自适应巡航控制（CACC）。此外，针对4级或5级自动化技术的研究通常并不假设具备联网能力。
第三，人类驾驶车辆与自动驾驶车辆的行为建模有所不同。交通领域使用不同的模型来区分人类驾驶车辆与自动驾驶车辆：人类驾驶车辆往往表现出不稳定、随机的行为，而自动驾驶车辆则可以通过稳定的控制器设计克服交通不稳定性。相比之下，由于机器人学界未考虑集体交通模式，他们认为人类驾驶员是自动驾驶车辆应模仿的智能体。因此，这些研究通常不区分人类驾驶车辆与自动驾驶车辆，而是将两者均建模为人工智能代理。
第四，关于自动驾驶车辆与人类驾驶车辆之间的交互建模存在差异。交通领域并未对自动驾驶车辆在驾驶过程中如何与人工驾驶车辆交互进行形式化描述。在微观层面，采用跟驰模型（CFM），隐式地编码了车辆如何跟随其直接或远距离前车的行为；在宏观层面，通常采用多类别交通模型，这些模型并未详细定义微观层面的交互。机器人学界则试图显式地设计一辆或多辆自动驾驶车辆与一辆或多辆人工驾驶车辆之间的微观交互。
总之，这两个领域以不同的目标、模型、算法和数据集来构建自动驾驶控制问题。

1.3. 基于物理的与基于人工智能的交通模型

基于物理的模型研究可追溯到20世纪30年代（格林希尔茨等人，1935），并在真实世界交通现象的建模与预测方面取得了突破（周和拉瓦尔，2019）。因此，即使本文的重点是基于人工智能的模型，也不应低估基于物理的模型的价值。由于参数数量较少，基于物理的模型易于标定；由于所有物理术语清晰明确，易于解释；并且在数学上通常易于处理稳定性

1.4 驾驶策略映射：概述

为了进一步说明两个领域的差异，我们提供了一个驾驶策略映射的通用数学形式。设S ⊆R m +和 A ⊆R n +分别为状态和动作空间，其中m ∈ N+和n ∈ N+分别为状态和动作向量的维度。驾驶行为模型，即驾驶控制或策略，是由θ参数化的数学映射，记为πθ，它将状态s ∈ S （即交通环境的观测）映射到动作a ∈ A （即加速度和转向角）：
πθ:s→ a (1.1)
映射πθ可以通过第一性原理（基于物理）或从数据中获得。我们在表2中总结了纵向控制策略的各种映射形式。我们在此选择纵向控制的原因是，这类模型被研究得最为广泛，并且近年来在将机器学习引入此类行为建模方面付出了大量努力。驾驶策略映射可分为基于物理的和基于人工智能的两类。基于物理的映射可以通过数学公式来描述，而基于人工智能的映射通常由各种机器学习模型表示。
在每种映射类型中，我们还比较了人类驾驶车辆与自动驾驶车辆建模方式的不同。如前所述，当人类驾驶车辆与自动驾驶车辆均采用基于物理的映射时，两者的主要区别在于参数，这反映了自动驾驶车辆具有更好的“感知”能力、“看得更远”，以及“反应更快”。
基于人工智能的映射假设存在一个从驾驶感知到机器执行的复杂且高度非线性的映射。在这些映射中，人类驾驶车辆与自动驾驶车辆之间的差异可能并不显著，因为其目标是训练自动驾驶车辆表现出类人性能。在倒数第二列中，我们列出了每个映射类别的相关领域及部分参考文献。文中列出的大多数参考文献将在后续章节中再次提及。在最后一列中，我们强调了每类模型的优点以及模型选择的推荐标准，总结于子章节（1.3）。
基于物理的驾驶模型被交通与控制领域广泛使用，假设每个单元的行为类似于自动粒子或自动机，其中人类认知过程和机器的机械动力学被高度简化。跟车是最受关注的驾驶行为，可分为三类：微观驾驶模型、中观交通流模型和宏观交通流模型。
微观模型通过单个车辆的位置、速度和加速度来描述其运动，假设车辆根据与直接前车的跟车距离、速度差和其他特征动态选择行驶速度和加速度。所使用的数学工具是常微分方程。一些广泛使用的微观跟车模型包括Newell（Newell, 1961）、Gipps模型（ Gipps, 1981）、IDM（智能驾驶员模型）（Treiber等人，2000；Kesting等人，2010）以及OVM（奥罗斯等人，2010；金和奥罗斯，2014；秦和奥罗斯，2017）。
宏观模型将交通视为连续流，其特征是总体交通密度和速度。交通密度和速度的演变通过偏微分方程来确定。流行的交通流模型包括LWR（Lighthill和Whitham，1955；Richards，1956）、PW（Payne，1971）和ARZ模型（Aw和Rascle，2000）。
微观模型连接微观与宏观模型，使用车辆速度的概率分布函数来表征交通流（vanWageningen‐Kessels等，2015）。最流行的微观模型是气体动力学模型（Hoo‐gendoorn，1999；Hoogendoorn和Bovy，2001；Hoogendoorn和HLBovy，2003）。由于微观模型缺乏明确的物理意义，并且无法直接应用于仿真，因此在交通领域中的研究不如其他模型深入。迄今为止，它们主要作为从相应的微观驾驶行为推导宏观模型的数学工具

1.5. 人工智能在自动驾驶车辆决策中的应用

与其明确假设自动驾驶车辆将如何驾驶，我们更认为未来的自动驾驶车辆应被设计为理性的、以效用最大化为目标的智能体，能够在各个驾驶选择层面采取最佳策略。通过这种方式，自动驾驶车辆能够根据即将发生的交通状况做出反应，并紧密模仿人类驾驶员的智能。然而，自动驾驶车辆相较于人类驾驶员的主要优势在于其能够更快地获取更全面的信息，从而比人类驾驶员以更优的方式做出反应。然而，真实交通实验成本高昂且风险极高。因此，我们寻求一种创新的AI-guided方法论框架，用于实现复杂的多智能体学习与适应。
尽管在计算机视觉方面投入了大量的机器学习努力，但自动驾驶车辆的智能体现在运动规划阶段的最优决策上。我们认为，赋予自动驾驶车辆驾驶智能的关键在于人工智能，甚至更广泛的“通用人工智能”（AGI）（拉马穆尔蒂和扬波尔斯基，2018）。我们正看到越来越多的研究采用人工智能方法来探索人类的驾驶行为，包括深度学习（田中，2013；科洛姆巴博尼和弗斯科，2014；周等， 2017a；王等，2018；朱等，2018a）、强化学习（范德韦尔夫等，2001）以及模仿学习（克弗勒等，2017；巴塔查里亚等，2018）。
最近，许多研究还集中于人类行为预测，例如换道（库马尔等，2013；吴等，2017；魏等，2019年；寿等，2020c）、汇入（里奥斯‐ 托雷斯和马利科波洛斯，2016；贝夫利等，2016）和停车行为（熊谷和赤松，2006），以高置信度预测人类何时会进行换道。然而，人工智能在自动驾驶汽车决策过程中的应用仍处于新兴阶段，且研究不足。
博弈论是建模理性参与者策略性交互的一个成熟领域，它增强了多个交互机器的智能，并正在变革人工智能领域（滕恩赫尔茨， 2002）。幸运的是，我们已经看到控制、交通和人工智能领域之间逐渐融合，这些领域已采用博弈论模型来为自动驾驶车辆设计算法决策过程（Yoo和Langari，2012；Yoo和Langari，2013；Kim和Langari，2014；Talebpour等，2015；Yu等，2018；黄等， 2019；黄等，2020a；黄等，2020b）。我们也相信，博弈式交通将成为未来自动驾驶车辆的一项关键特征，以在复杂交通环境中实现战略性交互并导航。

1.6. 论文结构

本文其余部分的组织如下：在第2节中，我们将提供混合交通中自动驾驶车辆控制的一般问题陈述，以及现有的知识空白。随后，我们将在第3–6节中分别考察现有的自动驾驶车辆控制模型与方法。第7节分别介绍人类与自动驾驶策略学习的方法与模型。第9节总结了所有已回顾的模型。在第10节中，我们提出使用人工智能方法进行混合交通建模所面临的挑战与见解，并指出了潜在的研究领域。

2. 面向自动驾驶车辆的人工智能引导驾驶策略学习

2.1. 具有混合自主性的多车系统（MVS）

混合交通系统由大量网络化智能体组成，包括自动驾驶车辆、人类驾驶员以及其他道路使用者（如行人和骑行者）。这些智能体在与交通环境交互的同时动态地选择驾驶行为。他们的行为是相互依赖的，即某一智能体的驾驶行为会通过耦合奖励函数、共同交通环境状态或动作约束而依赖于其他智能体的行为。由于这种智能体间耦合关系，混合交通系统构成一个多智能体系统（MAS）——这是控制与机器人学界广泛使用的术语。具体而言，我们将其称为“多车系统（MVS）”。接下来，我们将以抽象的方式阐述MVS的高层级自动驾驶车辆控制问题。
定义2.1（混合自主性多车系统的自动驾驶车辆控制问题陈述）。 在混合交通的多车系统中，有N个可控自动驾驶车辆（AV），其索引
为n ∈{1,2,…,N}，沿一段道路行驶，初始状态为s(1) 0 ,…,s(N) 0 。第nth辆车的目标是在预定义的规划时域[0,T]内，在离散时间间隔（即
a(n) 1 ,…,a(n) T）或连续时间（即a(n)(t),t ∈[0,T]）中选择一系列最优驾驶控制（包括加速度和/或转向角）。在此通用设定下，我们可
以定义自动驾驶车辆控制问题的建模方式以及每辆车的状态更新方式。本文将主要介绍离散时间版本，但该模型可轻松推广至连续时间版本。
控制优化: MVS的自动驾驶车辆控制问题是从状态s={s (n) t}n=1, … ,N t∈[0,T] 到动作a={a (n) t}n=1, … ,N t∈[0,T] 建立一个由θ 参数化的驾驶
策略映射πθ( ⋅)。
根据控制模型的选择，这种映射可以被定义为动力系统、最优控制问题或模型预测控制（MPC）（由交通与控制学界提出）、博弈论模型（由机器人学界提出），或基于人工智能的模型（由机器人与控制领域提出）。

2.2. 研究问题

根据上述定义的问题组成部分，我们希望明确四个主要研究问题，这些问题将指导本文后续方法论综述的展开。
问题1 在由人类驾驶员和非自动驾驶车辆组成的混合交通中，应采用何种可扩展的驾驶策略来控制大量自动驾驶车辆 - 可控自动驾驶车辆？（第3–6节）
问题2 如何估计人类驾驶员行为？（第3–6节）
问题3 在环境中应如何建模不可控自动驾驶车辆的驾驶行为？（第3–6节）
问题4 人类驾驶员与自动驾驶车辆之间的交互如何表征？（第3–6节）

备注2.2。 （Q1）涉及如何建立驾驶控制策略的映射关系。（Q2，Q3）与状态更新动态相关，旨在对周围道路使用者行为进行准确建模和预测。（Q4）涉及所选择的驾驶控制策略如何影响其他道路使用者，反之亦然，这为自动驾驶车辆控制提供了反馈，并决定了状态更新动态。

2.3. 导航路线图：控制维度

在接下来的章节中，我们将概述现有文献如何解决这些车头间距问题。我们根据涉及的自动驾驶车辆和人工驾驶车辆的数量对这些研究进行分类，包括：一辆自动驾驶车辆与一辆人工驾驶车辆交互（1AV+ 1 HV），一辆自动驾驶车辆在以人工驾驶车辆为主的交通环境中行驶，即一辆自动驾驶车辆与多辆人工驾驶车辆交互（1AV+ mHVs），多辆自动驾驶车辆与多辆人工驾驶车辆交互（nAVs+ mHVs，n ≪m），多辆自动驾驶车辆与一辆人工驾驶车辆交互（nAVs+ 1 HV），以及纯自动驾驶汽车市场（nAVs）。
除了自动驾驶车辆（AV）和人工驾驶车辆（HVs）的数量外，我们还基于两个维度对多自动驾驶车辆控制问题进行分类：第一个维度是这些可控自动驾驶车辆（AV）是否具有合作性，第二个维度是自动驾驶车辆控制是否考虑来自外部环境的不确定性。
在接下来的第3–6节中，我们将以涉及的自动驾驶车辆和人工驾驶车辆数量作为主要分类，车辆协作作为次要分类，环境随机性作为第三级分类，对文献进行分类。
由于相关研究范围广泛，为了引导读者查阅混合交通中自动驾驶车辆控制的文献，图2提供了一个路线图，指向各个（子）节。
示意图1

彩色矩形代表分类标准，红色圆角矩形（作为终端节点）代表用于控制自动驾驶车辆的方法。

备注2.3。
1. 当仅存在单个需要被控制的自动驾驶车辆时，自动驾驶车辆之间的合作或竞争不存在。因此该类别将在第3 （“1辆自动驾驶汽车+ 1人类驾驶车辆”）和第4 （“1辆自动驾驶汽车+m辆人类驾驶车辆”）中跳过。
2. 在第5节（“n辆自动驾驶车辆”）所讨论的纯自动驾驶汽车市场中，大多数研究假设环境是确定性的，因为所有自动驾驶车辆都可控制且完全可观测（对于网联自动驾驶汽车而言），而随机性可能源于测量误差或通信延迟。在第3, 4,6节涵盖的混合市场中，由于人类驾驶行为的随机性，环境通常是随机的，但在某些场景下，如车队编组或在封闭环境中行驶，也可能会假设为确定性环境。

3.1 1辆自动驾驶车辆þ1辆人类驾驶车辆，1辆自动驾驶车辆þ1辆自动驾驶车辆

在本节中，我们将根据由一辆人类驾驶车辆（HV）或自动驾驶车辆（AV）构成的交通环境是确定性的还是随机性的，对模型进行分类。在这两种情况下，现有文献中均采用了基于博弈的控制。博弈论是建模自动驾驶车辆之间或一辆自动驾驶车辆与一辆人类驾驶车辆之间非合作性战略交互的自然方法，这些车辆通常被视为旨在优化个体目标函数的智能体。在博弈论框架中，车辆被称为“智能体”或“参与者”。

3.1. 确定性环境：一次性博弈

一次性双人博弈被用于建模两辆车的单步策略行为。驾驶（Yoo和Langari，2012）、汇入（Liu等，2007；Yoo和Langari， 2013）、变道（Talebpour等，2015；Yu等，2018；张等，2019c；Yoo和Langari，2020）以及无保护左转行为（Rahmati和 Talebpour，2017）被建模为双人非零和非合作博弈（Liu等，2007；Talebpour等，2015）、斯塔克尔伯格博弈（Yoo和 Langari，2012；Yoo和Langari，2013；Yu等，2018；张等，2019c；Yoo和Langari，2020）或混合动机博弈（Kim和 Langari，2014）。这些博弈的结果可以是基于收益双矩阵的纯策略或混合纳什均衡。特定策略的收益取决于当前行驶速度、相对位置、反应与感知时间、激进程度和碰撞避免，反映了交通安全与效率。在对人类驾驶行为进行建模时，通过收集驾驶员数据，并采用双层优化（Liu等，2007）、模拟矩方法（Talebpour等，2015）和最大似然估计（Rahmati和Talebpour，2017）来估计收益函数的参数。当博弈参与者之一为自动驾驶车辆时，需考虑周围驾驶员的激进程度，设计相应的效用或奖励（Yoo和Langari，2020）。
Zhang et al.(2019c)进一步开发了一种基于博弈论的模型预测控制器，该控制器
连续求解多个交互车辆的斯塔克尔伯格均衡。

3.2. 随机环境：动态博弈

一次性博弈无法对车辆的动态驾驶行为进行模型化。为求解时变控制，已针对自动驾驶车辆提出了动态最优控制（王等人，2015）、模型预测控制（MPC）（王等人，2016；龚等人，2016；龚和杜，2018）或滚动时域控制（Swaroop等人，1994；王等人， 2014a；王等人，2014b；周等人，2017b）。当一个智能体在求解最优控制问题的同时，其交互代理也在以冲突目标求解最优控制问题时，便形成了微分博弈（王等人，2015）。微分博弈对具有冲突目标的交互代理的动态行为进行建模，其中智能体的最优策略来源于最优控制问题。
如果自动驾驶车辆能够预测人类驾驶车辆在整个规划时域内的战略，那么它将优化自身的目标函数，该目标函数取决于其自身当前和未来的战略以及人类驾驶车辆当前和未来的战略，从而生成沿此规划时域的一系列连续控制策略并加以实施。同样的过程适用于人类驾驶车辆。由于存在动态耦合，求解这种均衡具有挑战性。因此，经典的微分博弈主要集中在两个参与者的情形，而对于超过两个参与者的均衡则变得难以处理。
为了简化，已应用了几种技术。萨迪格等人（2016b），拉扎尔等（2018a）已将原始的双玩家微分博弈简化为在离散时间步长上进行的领导者–跟随车博弈（或斯塔克尔伯格博弈）。在此博弈中，自动驾驶车辆首先采取动作。然后，人工驾驶车辆观察自动驾驶车辆所采取的动作，并基于自动驾驶车辆的历史动作预测其未来动作，最大化自身目标，并计算自身在未来一段时间内的动作。随后，自动驾驶车辆利用人工驾驶车辆的未来动作来最大化自身目标，并在每次迭代中使用模型预测控制反复重新规划。换句话说，在领导者–跟随车框架中，自动驾驶车辆直接基于对人类驾驶员行为的预测求解一个优化问题，而非基于人类’的实际策略。斯塔克尔伯格博弈的优势在于，可以通过精心设计的奖励函数预先设计自动驾驶车辆以影响不受控的人工驾驶车辆（Sadigh等，2016b）。奖励函数包含两部分：一部分控制自动驾驶车辆的驾驶效率和安全，另一部分决定自动驾驶车辆希望对相邻人工驾驶车辆施加的影响。拉扎尔等（2018a）将该框架扩展到一个自动驾驶车辆与多个人工驾驶车辆之间的斯塔克尔伯格博弈，但假设一个自动驾驶车辆仅影响一个人工驾驶车辆，而其他人工驾驶车辆的动作是固定的。
菲萨克等人（2019）进一步开发了一种分层博弈论规划方案，其中战略规划器在相对较长的规划时域（例如5秒）内求解具有近似动力学的闭环动态博弈，而战术规划器则在较短的规划时域（例如0.5秒）内基于高保真车辆动力学求解开环轨迹优化。在战略规划层面，自动驾驶车辆与人类驾驶车辆仍进行反馈斯塔克尔伯格动态博弈，其驾驶行为通过动态规划的连续应用递归求解。从战略层面求得的最优Q值随后被引入战术层面的目标函数中，作为表示最优未来奖励的引导性终端奖励。在战术规划层面，自动驾驶车辆的轨迹通过嵌套优化问题迭代优化，该问题在短期规划范围内估计人类’对每个候选方案的最佳轨迹响应。该分层博弈论模型在两种场景下进行了测试：合流与超车操作，一种是在仅存在双车交互的笔直空旷多车道高速公路上，另一种则额外包含第三辆车（即一辆速度较慢的卡车）。
在存在对抗性风险的随机环境中，已采用对抗学习博弈来建模人机交互并训练鲁棒自动驾驶控制器。假设人类驾驶车辆为对抗者，试图干扰自动驾驶车辆的动作，萨迪格等人（2019）首先利用最大熵逆强化学习方法学习人类驾驶车辆动作背后的奖励函数，然后通过嵌套优化计算序列自动驾驶控制。

4.1 自动驾驶车辆与m个人类驾驶车辆

在本节中，我们将根据由一定数量的人工驾驶车辆构成的交通环境是确定性还是随机性来划分模型。在确定性

4.1. 确定性环境

4.1.1. 基于稳定性的控制

When the environment is 确定性的，交通控制领域旨在研究一辆自动驾驶车辆如何利用线性（崔等人，2017；Wang，2018）或非线性控制器（金和 Orosz，2014；金和奥罗斯，2018）来稳定人工驾驶车辆车队，其依据是头尾串行稳定性（即车队中从第一辆车到最后一辆车的稳定性（金和Orosz，2014））。实地实验也证明了使用一辆自动驾驶车辆稳定人工驾驶车辆的可行性（斯特恩等人，2018；金和奥罗斯，2018）。以稳定性为导向的方法更广泛地应用于多辆网联自动驾驶车辆车队的场景，因此更多相关研究将在第5章（“n辆自动驾驶车辆”）和第6.1.1节（“n辆自动驾驶车辆+ m辆人工驾驶车辆”）中介绍。

4.1.2. 基于博弈的控制

Assume the HV-domin 在确定性环境中，每辆车都在博弈论框架下相互作用，自动驾驶车辆与多个人工驾驶车辆之间被建模为同时一次性博弈或微分博弈。
张等(2019c)、科斯昆等(2019)、张等(2019b)提出了一种针对自动驾驶车辆在人工驾驶车辆主导的交通流中执行强制变道的一次性斯塔克尔伯格博弈序列。目标是训练自动驾驶在间隙接受和变道方面具备类人性能。人工驾驶车辆通过IDM（Zhang等，2019c）建模，或作为博弈参与者建模（张等(2019b);Coskunetal.,2019）。设计了分层控制架构：高层控制器估计周围人工驾驶车辆的激进程度，并与自动驾驶车辆邻域内的每一辆人工驾驶车辆进行斯塔克尔伯格博弈。选择带来最高奖励的斯塔克尔伯格博弈策略（包括变道时间与行驶加速度）作为最优驾驶策略，并将其输入到底层控制器。底层控制器采用模型预测控制，根据当前和未来的奖励更新被控车辆’的位置。构建了基于MATLABSimulink的人在环仿真器（张等(2019b);Coskunetal.,2019），参与者在虚拟多车道高速公路环境中操控人工驾驶车辆。
施瓦廷等(2019)通过求解嵌入隐性协商层次的迭代最优响应，开发了一种自动驾驶控制策略。在双主体情况下，迭代最优响应可表示为a(AV)(a(HV)(a(AV)(⋯)))。在多车系统中，利用KKT条件将相互依赖的优化系统简化为单层优化。所得到的纳什均衡不仅为自动驾驶车辆提供了控制律，还预测了其他人工驾驶车辆的动作。该研究的创新之处在于将“社会价值取向(SVO)”这一术语引入人工驾驶车辆的奖励函数中，用以表征人工驾驶车辆的驾驶激进程度。在与另一车辆交互时，可调整其SVO值。该控制律已在高速公路汇入和无保护左转场景中得到验证。社会偏好学习可使自动驾驶车辆的性能提升25%。
为了解决同时建模大量人类驾驶车辆的挑战，刘和富塚（2015，2016）将多个人类驾驶车辆组合为一个有效智能体，并假设一个序贯博弈，其中人类驾驶车辆处于主导地位，自动驾驶车辆采取反应性策略。通过将基准控制律映射到一组安全控制，开发了一种在线算法，使自动驾驶车辆控制器能够将人类意图作为安全约束加以考虑。

备注 4.1。 对于“1辆自动驾驶车辆+m辆人工驾驶车辆”的场景，使用基于博弈论的控制的研究较少，部分原因是耦合博弈系统的高维性。与将每辆人工驾驶车辆视为智能体不同，大多数研究将所有这些人工驾驶车辆视为自动驾驶车辆运行的随机环境。因此，基于深度学习和强化学习的自动驾驶车辆控制被建模，这将在本节余下部分占据主要篇幅。

4.2. 随机环境

4.2.1. 基于深度学习（深度学习）的控制

Prior to the prevalence of reinforcem 在学习领域，（深度）监督学习是一种流行的工具，用于训练自动驾驶车辆的无模型和端到端控制器，它可以直接将传感器输入映射为控制指令。行为克隆（BC）将自动驾驶车辆策略学习简化为一个监督学习问题，当驾驶数据充足或驾驶任务局限于有限区域时，通常表现良好。波梅罗（1989）提出了一种从模拟道路图像中学习的多层网络，以控制车辆在真实道路上行驶。自动驾驶车辆的下一个里程碑是采用卷积神经网络（CNN）高效处理原始相机图像，使自动驾驶车辆在类似场景训练后能够通过充满障碍物的道路（穆勒等人，2006）。此后，基于卷积神经网络的自动驾驶车辆控制器被广泛研究，近期的工作包括NVIDIA’的PilotNet（博加尔斯基等人，2016；博加尔斯基等人，2017），用于在真实交通状况下控制自动驾驶车辆；劳施’的深度卷积神经网络策略（劳施等人，2017）和 DeepPicar（贝希特尔等人，2018）用于转向角控制；潘等人（2018）提出的敏捷驾驶（Agiledriving）用于激进场景下的转向角和速度控制。为了提升自动驾驶车辆控制性能，研究中已考虑驾驶数据的时间依赖性，近年来长短期记忆（LSTM）及其变体已被应用于端到端自动驾驶车辆策略学习。徐等人（2017）提出了FCN‐LSTM，即全卷积网络（FCN）与LSTM的结合，可预测未来车辆自运动数据的分布。–伊拉基等人（2017）开发了卷积LSTM（C‐LSTM），用于学习驾驶过程中的视觉与动态时间依赖性。海克尔等人（2018a）提出了Drive360，该方法结合卷积神经网络、全连接层和长短期记忆网络，融合多个传感器的信息以预测驾驶操作。班萨尔等人（2019）提出了ChauffeurNet，一种中到中驾驶策略学习框架，其中输入信息在送入循环神经网络（RNN）生成低层控制之前经过预处理。

4.2.2 基于强化学习的控制

在以人工驾驶车辆为主的交通中，单个A V的驾驶策略选择可以被视为一个序列决策过程部分或完全可观测的随机环境。需要学习驾驶策略，以利用车辆的环境信息作为输入来预测其加速度和转向角。
强化学习（Sutton and Barto, 1998）使智能体能够通过奖励驱动学习最优策略，在游戏播放领域取得了突破性进展，例如 AtariMnih et al.(2015)、围棋（Silveret al., 2016）、扑克（BrownandSandholm,2018;BrownandSandholm,2019年）、 Dota2（OpenAI, 2018）以及StarCraftII（Vinyalsetal.,2019年）。其在自动驾驶领域的应用已成为一个有前景的方向。
当在随机环境中使用强化学习控制自动驾驶车辆时，其基本思想如图3所示。我们首先讨论单智能体强化学习场景。一辆可控的自动驾驶车辆（即需要设计控制器的主车辆）感知由人类驾驶车辆、其他不可控的自动驾驶车辆以及道路使用者组成的混合交通环境的状态。根据某个预定义的奖励函数，该车辆执行一个动作（例如加速度或转向角），从而改变交通环境的状态。作为反馈，环境向该自动驾驶车辆提供一个奖励。基于接收到的奖励和新的环境状态，自动驾驶车辆进一步求解基于奖励函数的最优策略并选择动作。
此过程不断迭代，直到自动驾驶车辆完成整个控制过程。当存在多辆自动驾驶车辆需要同时做出决策时，我们需要采用多智能体强化学习（MARL）框架，这将在第6.2节中讨论。
MDP隐含地假设智能体能够完全观测到状态动态。换句话说，在智能体执行一个动作后，他知道系统将转移到下一个状态的概率。大多数交通研究假设车辆之间通过V2V或V2I实现联网。得益于这些通信技术，每位驾驶员都能获得其他驾驶员和系统状态的完整信息。而控制与机器人学研究人员则对可观测性做出了各种假设（Liu和Tomizuka,2015；Liu和Tomizuka,2016；Liu等人， 2018年；布顿等人，2017；布顿等人，2018年）。人们可以观测到其他车辆的’位置、航向，有时还包括纵向和横向速度，但无法观测到加速度。即使一名驾驶员能观测到其他驾驶员的全部状态，她也可能不知道这些驾驶员的意图。因此，自动驾驶车辆必须基于自身的观测，在所有可能的状态上维持一个信念状态空间。因此，部分可观测马尔可夫决策过程（POMDP）模型被广泛用于建模单个自动驾驶车辆’的运动规划，以及在以人工驾驶车辆为主的交通中的单车自动驾驶控制问题。
当交通动态过于复杂而无法用POMDP建模时，无模型方法如深度强化学习（DRL）被广泛采用。为了实现自动驾驶车辆的无模型训练，需要一个仿真器来提供具有因果关系的信息，例如奖励和交通状态更新，以便自动驾驶车辆从中学习。吴等人（2017b）使用深度强化学习（DRL）训练自动驾驶控制器，并采用指定的奖励函数以避免与其他智能体发生碰撞，同时应用信赖域策略优化（ TRPO）方法在SUMO仿真器中训练高斯多层感知机（MLP）策略，以提高交通效率。Lillicrap等人（2015）将深度确定性策略梯度（DDPG）强化学习算法应用于仿真环境中对车辆的控制。他们的研究设计了一种奖励函数，该函数在每一步根据车辆沿车道方向投影的速度给予正向奖励，并对碰撞施加− 1的惩罚。Sallab等人（2017）开发了一种集成深度Q网络（DQN），该网络结合注意力模型以利用局部观察，并通过动作网络引导CNN卷积核生成TORCS仿真器中的转向指令，该仿真器针对在/偏离车道的情况提供正/负奖励。Perot等人(2017)提出了一种异步优势Actor‐Critic（A3C）方法，用于在逼真游戏（如世界拉力锦标赛6和TORCS仿真器）中训练策略网络。这项工作由Jaritz等人(2018)进一步改进，获得了更好的收敛性和泛化能力。这两项研究都将奖励设计为距道路中心距离以及道路与车辆’航向之间角度的函数。除了惩罚碰撞和偏离车道等常见的奖励函数外，Landolfi和Dragan（2018）引入了一个额外的奖励项，即社会协同奖励，该奖励项学习从周围人类驾驶员提取的社会特征的均值和方差。这一额外的奖励项使自动驾驶车辆能够学习社会可接受的策略，并使其自身行为与邻近车辆保持一致。这种社会协同驾驶在不成文的驾驶规则占主导地位的场景中进行了测试，例如出现救护车以及所有人都在超速的情况下。
蒙特卡洛树搜索（MCTS）是解决在线决策问题最有效的方法之一（Browne等人，2012），近年来已被应用于自动驾驶车辆。帕克森等（2017）将MCTS与在线性时序逻辑（ITL）约束下训练的分层神经网络控制策略相结合，用于复杂道路环境中的运动与路径规划。他们设计的奖励函数由基于当前连续状态（例如位置或速度）的代价项组合、基于完成即时目标（例如在标志处停车或离开某个区域）的奖励项以及违反约束的惩罚项构成。Sunberg等人（2017）使用MCTS推断交通参与者的内部状态，以在高速公路上执行安全变道。他们的奖励机制设计对自车到达目标车道所需的平均时间以及在此期间任何车辆执行的紧急制动操作次数进行惩罚。 Hoel等人（2020）将MCTS与深度强化学习（DRL）结合以实现战术高速公路驾驶，在他们的研究中，一个深度神经网络被训练用来引导MCTS到搜索树的相关区域，同时MCTS也被用于改进神经网络的训练过程。相应的奖励是关于变道次数和与期望速度差异的代价项组合，以及高速公路出口的奖励项（即目标达成）。
基于深度强化学习的自动驾驶车辆控制还有另一个方向，即利用先验知识或经典理论驱动控制器来约束基于神经网络的驾驶模型的学习和行为。Bouton等人(2017)在奖励函数中引入计算安全因子作为惩罚项，而不是作为硬约束（布顿等人，2017），因此从马尔可夫决策过程中求解出的驾驶策略无法避免事故。Bouton等人(2018)增加了一个模型验证步骤，以对强化学习智能体训练后的驾驶策略施加概率保证，并使用简化奖励函数来惩罚动作步骤的数量并奖励目标达成。Zhang等人(2016)提出在引导策略搜索框架中将传统MPC方法与强化学习相结合，用于控制自主飞行器，其中使用由MPC生成的数据训练深度神经网络策略，以实现训练鲁棒性和可泛化控制。该强化学习训练基于一个成本函数，用于衡量策略模型生成的动作与MPC生成数据之间的分布差异。Chen等人 (2019b)提出了一个分层控制框架，其中高层

4.3. 基于人工智能的模型的对抗性攻击与网络安全

在迈向混合自主性时代的过程中，假设存在对已开发的良性自动驾驶车辆和网联自动驾驶汽车系统产生负面影响甚至故意攻击的恶意人工驾驶车辆和不可控自动驾驶车辆，并非无关紧要。若缺乏对与（网联）自动驾驶车辆相关的对手的深入理解以及有效防御方法的开发，就无法建立安全高效的混合交通生态系统。本节回顾了两类最重要的与（网联）自动驾驶车辆相关的攻击——网络攻击和深度学习攻击，并探讨了现有研究如何被用来缓解这些问题。
自动驾驶车辆容易受到对抗性网络和深度学习攻击，特别是当我们迈向网联自动驾驶汽车系统时。网联自动驾驶汽车的网络安全面临着网络攻击的挑战，包括但不限于真实性攻击（杜克尔，2002；阿穆扎德等人，2015；何等人，2015；乌卡尔等人，2017；利亚明等人， 2018）、网络层攻击（加里普等人，2015；卡尤姆等人，2020）以及系统级攻击（舒克里等人，2013）。由于这些攻击主要针对物理通信层而非网联自动驾驶车辆控制器，本文将不详细讨论这些方法。感兴趣的读者可参考拉吉巴胡尔等人（2018）以获取更多细节。
随着深度学习（DL）成为自动驾驶车辆（AV）系统的核心，对抗性攻击可能同时发生在自动驾驶车辆运行的物理世界以及需要处理信息并执行计算的数字世界中。攻击算法及其变体已被应用于目标检测、传感器融合和深度强化学习等领域。特别是图像识别与分割，直接关系到自动驾驶车辆通过摄像头处理图像信息以识别和检测交通标志、交通信号及周围物体的能力。最近已有研究展示了在此领域成功的攻击案例。宋等人采用鲁棒物理扰动算法生成被扰动的“STOP”标志，使该标志对最先进的YOLO模型保持不可见艾克霍尔特等人（2018）。昂等人研究了一种称为快速梯度符号法（FGSM）的方案（古德费洛等人，2014b），用于生成对抗性交通标志，以欺骗基于深度神经网络的交通标志识别模型（昂等人，2017）。张等人展示了仿真器如何对车辆应用伪装，以最小化检测分数并欺骗基于图像的目标检测器（张等人，2018a）。西塔瓦林等人设计了‘’有毒”标志，例如看似无害的人类观察者但能欺骗自动驾驶车辆交通标志识别机制的恶意广告和标志西塔瓦林等人（2018a），西塔瓦林等人（2018b）。
多传感器融合（MSF）被广泛认为是自动驾驶车辆更安全的感知系统，因为它结合了来自多个传感器（如激光雷达（光检测和测距）和摄像头）的感知结果，从而实现更高的整体精度和鲁棒性。然而，最近研究表明该系统也可能被欺骗。曹等人提出了一种名为 MSF‐ADV的攻击设计，用于生成能够在物理世界中同时欺骗基于激光雷达和摄像头的感知的对抗性三维物体曹等人(2020)。在演示中，他们使用3D打印机打印出设计好的三维物体，并将其放置在道路中央。这种对抗性物体能够欺骗基于深度神经网络的目标检测模型（针对激光雷达和摄像头），因此，对于采用先进的多传感器融合算法的受害自动驾驶车辆而言，该物体完全不可见。结果，受害自动驾驶车辆将忽略此物体并直接撞上它。
除了感知系统外，基于深度强化学习的自动驾驶车辆控制器也可能遭受攻击，从输入扰动到模型攻击均有可能。大多数深度强化学习攻击都基于输入扰动。Behzadan和Munir（2017年）设计了输入扰动，以在深度Q网络的训练阶段操控其策略。黄等人应用快速梯度符号法攻击使用深度Q网络、异步优势演员‐评论家（A3C）和信赖域策略优化（TRPO）训练的前馈策略（Huang et al., 2017）。林等人提出了“诱惑”攻击，通过生成一系列对抗样本及其相应的动作序列，将深度神经网络策略诱导至恶意设计的状态（ Lin et al., 2017）。
除了输入扰动之外，针对深度强化学习的基于模型的后门攻击研究也开始蓬勃发展。这些后门攻击通过微小的数据投毒（例如，仅占训练数据的0.025%）和带内奖励修改在训练阶段被植入策略中，且不会影响正常输入上的奖励。数据投毒会导致恶意行为，这些行为处于休眠状态，直到特定触发器出现才会激活，使得此类攻击极具隐蔽性。由于触发器设计不依赖于数据集，因此具有较高的灵活性。相关研究包括TrojDRL，该研究提出对策略实施后门攻击，在目标性和非目标性场景下，攻击未触发时其表现与良性策略几乎无法区分，但一旦触发则性能急剧下降Kiourti等人（2019年）。王等人（2020b）研究了基于深度强化学习的交通拥堵控制系统中的后门攻击，利用传感器数值作为触发器来激活对基于深度强化学习的自动驾驶车辆控制器的攻击，包括引发恶意的车辆减速和加速行为，从而导致走走停停的交通波产生（拥堵攻击），或导致自动驾驶车辆加速而撞上前车（保险攻击）。
针对深度学习对抗攻击的研究，提出了对抗训练范式以开发对抗性鲁棒深度学习解决方案，即对抗防御方法。正如Goodfellow 等人（Goodfellow et al., 2014b）首次提出，通过对抗样本进行学习可使深度神经网络具备抵御对抗性攻击的能力。对抗样本是一类通过对数据集中的样本施加微小但刻意设计的最坏情况扰动而形成的输入，使得扰动输入导致模型以高置信度输出错误答案。在深度学习中蓬勃发展的这些对抗防御方法，有望在（联网）自动驾驶车辆系统中实现鲁棒应用。特别是，开发对抗性鲁棒目标检测系统可以防止攻击者试图夺取（联网）自动驾驶车辆的控制权以引发事故（Qayyum et al., 2020）。萨迪格等人（2019）采用这一概念来建模一种博弈论交互：人类驾驶车辆作为自动驾驶车辆的对抗方，与自动驾驶车辆进行一场对抗性博弈。其目标是寻找一系列可能导致自动驾驶车辆出现不安全行为的人类驾驶行为。在此博弈中，自动驾驶车辆采取动作以最大化其累积奖励，而人类驾驶车辆则试图通过选择能够最小化自动驾驶车辆奖励函数的驾驶行为，来破坏自动驾驶车辆的动作。然而，设计、实现和实验验证具有对抗性鲁棒性的

5. n辆自动驾驶车辆：一个无人驾驶的世界

单个自动驾驶车辆的控制远不足以充分发挥自动驾驶车辆在混合自主时代的潜力，尤其是在越来越多自动驾驶车辆被引入公共道路的情况下。近年来，包含多辆自动驾驶汽车的系统引起了越来越多的关注。在本节及下一节中，我们将逆向讨论自动驾驶汽车部署的时间线：首先探讨被称为“n辆自动驾驶车辆”的纯无人驾驶世界，然后讨论混合市场（n AVs+ m HVs）。纯自动驾驶汽车市场先于混合市场，因为前者可以通过添加由人工驾驶车辆组成的交通背景而推广至后者。

5.1. 合作的控制

5.1.1. 确定性环境：基于稳定性的控制

A majority of research on control of multiple AVs falls 属于协同协调类别。换句话说，假设自动驾驶车辆之间相互通信以获取全局交通信息，并优化交通流改善的共同目标。协同控制在多机器人系统中已得到广泛研究。群体智能（Bogue,2008；Venayagamoorthy和Doctor,2004）、编队控制（Chen和 Wang,2005）以及一致性控制（Zegers等人，2017；Li等人，2018c）已被广泛用于具有集中式目标的机器人组协作完成任务，同样也应用于多自动驾驶车辆控制（吴等人，2018；Lazar等人，2018b）。
在协同MVS中，车辆的运动由中央控制器或规划器协调，以实现共同目标，例如集体稳定交通流并缓解交通拥堵（王等人， 2016；龚等人，2016；龚和杜，2018），优化驾驶舒适性（王等人，2014b；周等人，2017b），或提高燃油效率（王等人，2014a；姚等人，2018）。为了实现协调，需要具备完全可观测性和完全可控性，这意味着所有车辆的’状态和控制对中央控制器是已知的，并且每辆车都可以通过集中式或分布式方式进行控制。车辆编队中的通信拓扑结构决定了CAV之间合作的程度（李等人，2014）。例如，可以为车辆编队设计控制协议，通过基于一致性的方法使其达到平衡状态。相应地，车辆之间的跟车耦合被建模为一个一致性问题，并采用分布式非线性时滞依赖控制算法来求解安全速度（李等人，2018d）。
假设前车与后车之间以及车队领头车与跟随车之间具备联网能力，协同自适应巡航控制包含两个
示意图2

控制策略：恒定间距（斯瓦鲁普和赫德里克，1996；达尔巴和拉贾戈帕尔，1999；斯瓦鲁普等人，2001）和恒定时间车头时距（伊安努和钱恩，1993；拉贾马尼和什拉多弗，2001；范阿雷姆等人，2006；Naus等，2010；范德韦尔夫等，2001；周等人，2017b；阿雷菲扎德和塔勒布普尔，2018；斯特恩等人，2018）。自动驾驶车辆纵向加速度控制也可使用非线性跟驰模型进行建模，相关内容将在第1.4节中讨论。上述所有研究均旨在开发一种队列稳定的跟驰控制器，以平滑交通流并防止走走停停波动。但这些研究均未考虑控制与物理安全约束（龚和杜，2018）。换句话说，车辆之间的交互未被显式建模（李等人，2018d）。为了显式地建模车辆间的物理交互，越来越多的文献将自动驾驶车队纵向控制建模为最优控制问题。基于线性间距策略或非线性跟驰模型的控制策略是最优控制问题的特例（王等人，2014b）。
近年来，关于在纯交通或混合交通环境中设计协同驾驶策略的文献呈指数级增长，包括匝道合流（周等人，2016；陈等人， 2020a；孙等人，2020；卡里米等人，2020）、换道（拉迪诺和王，2020）、环岛驾驶（赵等人，2018）、信号交叉口编队行驶（姚和李，2020）以及道路网络交通组织（王等人，2020a；陈等人，2020b；林等人，2020）。这些研究主要集中在高层级的轨迹优化与运动规划上，并基于一个理想的基本假设，即网联自动驾驶车辆控制器能够精确且完美地实现所求解的轨迹，而不受环境不确定性或扰动的影响。
集中式控制要求中央控制器在每个时间步长为每辆车求解最优控制。这类集中式控制的求解具有挑战性，原因在于：（1）所有车辆的状态与控制通过目标函数与约束相互耦合；（2）更长的规划时域需要对未来交通动态进行预测，而这可能受到维度灾难和干扰的影响。
为了解决状态耦合的第一个问题，通常在每辆车辆上设计并实现一种分布式算法（王等人，2016；龚等人，2016；龚和杜， 2018；李等人，2018d；姚和李，2020）。基于一致性的方法也被用于设计控制协议，使车辆编队达到一致性，并设计了一种分布式的非线性时延相关控制算法以求解安全速度（李等人，2018d）。为了解决预测时域的第二个问题，原始的最优控制问题可以被近似为单步模型预测控制，并开发了一种分布式算法。当规划时域较短时，模型预测控制接近最优控制策略，但当规划时域较长时可能会偏离。模型预测控制还被用作高层控制模型来计算参考规划轨迹（王等人，2014a；王等人，2014b；龚等人，2016；龚和杜，2018；周等人，2017b）。感兴趣的读者可参考李等人（2014）获取关于基于稳定性的控制的全面综述。

5.1.2. 随机环境

The optimal control framewo rk可以通过多种方式扩展。当存在测量误差或仅具有部分可观测性时，将测量方程引入状态空间模型（王等人，2014a；王等人， 2014b；周等人，2017b）。考虑到由数据包丢失引起的随机通信延迟，提出了分解方法用于大型网联自动驾驶车辆系统的稳定性分析（秦和奥罗斯，2017；金和奥罗斯，2018；金等人，2018年）。将最优控制问题在空间域而非大多数基于最优控制的系统所采用的时间域中进行建模，张等人（2020）设计了一种针对数据包丢失和通信延迟的鲁棒CACC控制器。

5.2. 非合作控制：确定性环境

与协同控制相比，自动驾驶汽车之间的非合作交互相对研究不足。多辆自动驾驶汽车的非合作控制被建模为N人博弈论模型。据我们所知，所有关于多自动驾驶车辆竞争控制的研究均假设为一个确定性环境。
第一类研究假设在特定场景（例如车队编组）中需要控制的自动驾驶车辆数量较少，换句话说，n是一个有限数。王等人（2015）将自动驾驶车辆的离散车道变换和连续加速度选择建模为一个微分博弈，其中智能体’的最优策略通过求解最优控制问题获得。微分博弈的结果是动态均衡。当耦合智能体的数量较大时，涉及N个参与者的此类动态均衡在数学上是难以处理的。为了解决这一问题，王等人（2015）将问题分解为有限个子问题，并对每辆车应用模型预测控制。德雷弗斯和格尔茨（2018）通过汇总所有车辆的目标函数来求解广义纳什均衡，这本质上是一种协同控制。由于基于博弈的控制存在可扩展性问题，上述所有研究都不得不将其应用限制在有限数量的自动驾驶车辆上。随着越来越多的自动驾驶车辆被部署到公共道路上，亟需一种可扩展且计算高效的算法来应对大量自动驾驶车辆控制器的需求。
另一类研究假设了一个更通用的交通场景，即大量自动驾驶车辆在交通系统中相互交互，换句话说，n趋于无穷。随着自动驾驶车辆群体的增长，平均场博弈（MFG）已被证明是N车微分博弈的一种可扩展模型（黄等，2019；黄等，2020a；黄等，2020b）。
MFG是一种博弈论框架，用于建模由大量理性效用优化智能体交互所产生的复杂多智能体动力学，这些智能体的动态行为由最优控制问题刻画（拉西里和利昂斯，2007；黄等人，2006）。通过利用大量交互个体所带来的“平滑”效应，MFG假设每个智能体仅对整体群体的密度分布做出响应并为之贡献。MFG在金融领域（Gu´eant等人，2011；拉沙佩勒等人，2010）、工程学（杰哈奇等人， 2016）以及行人流（拉沙佩勒和沃尔弗拉姆，2011）中变得越来越流行。在自动驾驶车辆的纵向控制中，每辆车反向求解其最优速度，其聚合效应由哈密顿–雅可比‐贝尔曼（HJB）方程表述；而平均场近似则推导出交通密度的演化，该演化通过一个正向时间的输运方程（也称连续性方程、流量守恒方程）求解。为求解该均
场均衡，从MFE导出的分布式速度控制器被证明是N‐车微分博弈的一个∊‐均衡。
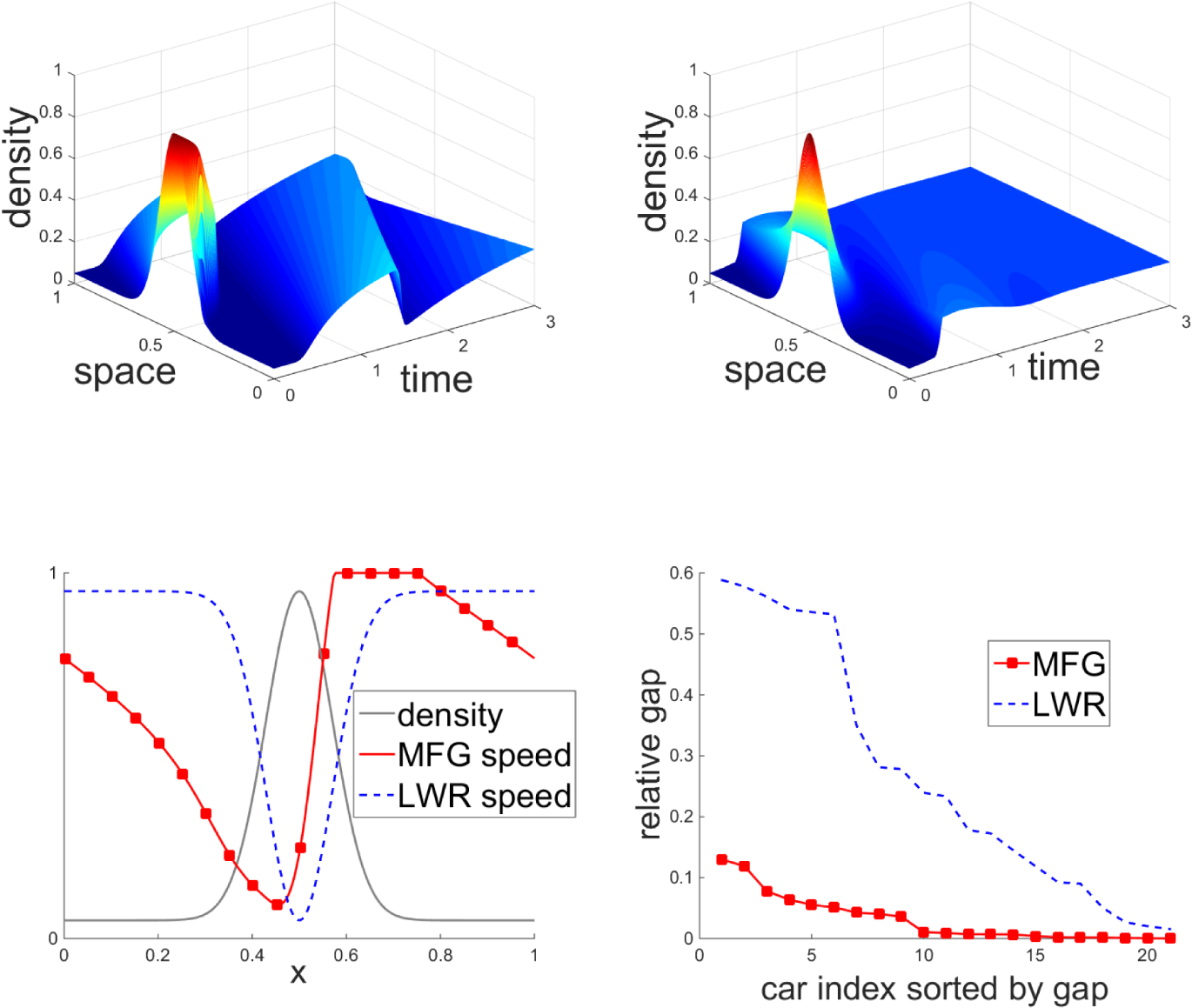
黄等人（2020a）还建立了基于均场博弈的宏观连续模型与现有交通流理论之间的联系。LWR模型隐含假设车辆按照流体动力学运动，而不对驾驶意图进行建模，已被证明是一种具有特殊设计目标函数的短视型均场博弈。综上所述，均场博弈通过行为解释体现了经典交通流模型，从而为容纳自动驾驶车辆等新型交通实体提供了灵活的行为基础和有前景的方向。在自动驾驶车辆更智能的目标函数下，LWR速度不再代表社会最优驾驶策略，如图4(d)中实际均衡偏离更大所示。图4(d)所示。图4(a‐b)表明，均场博弈控制器比 LWR控制器更快地缓解交通振荡。图4(c)揭示了某一时刻的原理。在具有对称交通密度的拥堵区域附近，由均场博弈控制器控制的车辆倾向于在进入拥堵区域前更早地在上游减速，并在离开拥堵区域后立即加速；而由LWR控制器控制的车辆在拥堵区域前后速度保持对称。这是因为LWR’的速度仅由该位置的交通密度决定，而均场博弈的速度取决于整个视野范围内的交通密度。

6. n辆自动驾驶车辆与m辆人工驾驶车辆：可控自动驾驶车辆（AV）在以人工驾驶车辆为主的交通中行驶

如前一节所述，在本节中，我们将人工驾驶车辆引入到多辆自动驾驶汽车行驶的交通环境中。同样，我们将使用车辆协作作为主要分类，环境随机性作为次要分类。

6.1. 协同控制

当多自动驾驶车辆控制是合作的时，现有文献涵盖了确定性和随机环境。

6.1.1. 确定性环境：多类别微观或中观交通模型

在第4.1.1节中，讨论了通过一辆自动驾驶车辆稳定多辆人工驾驶车辆的以稳定性为导向的控制。当自动驾驶车辆数量增加时，混合车队的稳定性在很大程度上取决于自动驾驶车辆与人工驾驶车辆的拓扑结构，包括车辆组成以及每种车辆类型的相对位置。由于从单车稳定性分析扩展到多类别交通组成的车队稳定性分析存在可扩展性问题，因此如何设计控制器以稳定混合交通车队仍属研究不足。
为了避免枚举混合车队的各种拓扑结构，大多数研究采用头尾稳定性的通用概念，其中车队的稳定性仅取决于自动驾驶车辆和人工驾驶车辆的总数，而不依赖于它们的拓扑结构（吴等人，2018）。通过仿真，塔勒布普尔和马赫马萨尼（2016）、姚等人（2019）在网联自动驾驶汽车上实现了协同自适应巡航控制，并研究了混合交通系统的串行稳定性。测试了不同的控制器参数以及网联自动驾驶汽车’的渗透率，以说明它们与稳定性的关系。
通过将整个车队分解为小型子系统，周等人（2020）提出了一种更实用的子系统头尾稳定性准则，并在新的稳定性准则下分析了包含多辆网联自动驾驶汽车和多辆人工驾驶车辆的混合交通系统。龚和杜（2018）求解了p步模型预测控制，而非单步模型预测控制，以减轻人类驾驶员轨迹的不确定性。
与实际上涉及车队瞬态行为的串行稳定性不同，控制领域常用两种更正式的稳定性概念，即李雅普诺夫稳定性和渐近稳定性（迪瓦约等人，2019；郑等人，2017；张等人，2020）。“李雅普诺夫稳定性”指的是平衡状态的小扰动仍保持在其附近，而“渐近稳定性” 指的是平衡状态的小扰动会收敛到该平衡点。在某种程度上，这两种稳定性概念比串行稳定性更通用，因为它们要求扰动车队中所有车辆的状态，而串行稳定性仅要求扰动车队领头车的速度。
为了分析多类型车队的稳定性，交通流稳定性（即随着时间增加，密度和速度分布在交通平衡状态附近的扰动幅度受到控制）（达尔巴和拉贾戈帕尔，1999；恩戈杜，2013b）被用作微观模型中串行稳定性的对应概念。已采用介观和宏观模型来表征交通流稳定性。恩戈杜等人(2009)、恩戈杜(2013b)、恩戈杜(2013a)采用气体动理学理论推导宏观网联自适应巡航控制交通流，并利用线性或非线性分析方法刻画稳定性图。波菲里等人（2015）对混合自适应巡航控制和协同自适应巡航控制车辆的宏观交通流进行建模，并分析自适应巡航控制车辆的渗透率如何影响
示意图3