微分方程杂记

微分方程的定义：

        通俗来说，就是等式中含有导数或者微分的方程，就叫做微分方程。（注意：等式中至少含有一个导数的表达式，或者微分的表达式，这样的式子才叫微分方程。）

微分方程的阶的定义：

        通俗来说，就是某个微分方程中，阶数最高的表达式的阶，就叫做微分方程的阶。

微分方程的解的定义：

        通俗来说，就是使得微分方程成立的函数，就叫做微分方程的解。

微分方程的解的分类：

        1.特解：通俗来说，特解就是确定了常数（也就是把C求出，含具体的常数）的解，叫特解。

        2.通解：通俗来说，含有任意常数（也就是C）的解，叫通解。

---

一阶微分方程：

        定义：微分方程中，导数或者微分最高为一阶。

        种类：

                       种类 1.可分离变量的微分方程：

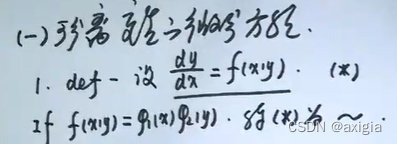
                        解法呢，通常就是把y的放一边，x的放一边，两边呢同时取积分，并且加C，然后进一步求解。

        

---

                        种类2.齐次微分方程：

                                

                                 例如：

                                解法：

---

 一阶齐次线性微分方程：

        齐次的含义：函数的最高次相同叫做齐次，齐次又叫做线性。

        形如：y'+P(x)y=0,这样的微分方程叫做一阶齐次线性微分方程。那么它的通解只需要公式代入即可了。

        公式就是：y=C(C为任意常数)

一阶非齐次线性微分方程（一阶当中最重要！）：

        形如：y'+P(x)y=Q(x),这样的微分方程叫做一阶非齐次线性微分方程。它的通解呢一阶非齐次线性微分方程的公式是另外一个。它就是：y=[+C](C为任意常数)

---

可降阶的高阶微分方程：

        种类：

                种类1：=f(x)，那么这样子的高阶微分方程求解呢，就只需要对它求对应n次的积分即可。

                种类2:f(x,y',y'')=0，这样的可降阶微分方程属于缺少y型，做法呢就是令y'=p,y''=dp/dx(也就是p'),就形成了一个以p为函数，以x为自变量的微分方程。代入公式，解出来的是p也就是y'，然后对这个p做积分就可得到y了。

                种类3：f(y,y',y'')=0，这样的可降阶微分方程属于缺少x型，做法呢就是零y'=dy/dx(也就是p),y''=p*(dp/dy)，进一步计算即可。

                例题：

---

高阶线性微分方程：

        种类：

                种类1：n阶齐次线性微分方程：

                        形如： （A式）

                种类2：n阶级非齐次线性微分方程：

                        形如：（B式），如果，就也可以拆成对应的两个子方程。

---

解的结构：

---

高阶常系数线性微分方程的解法：

        二阶常系数齐次线性微分方程及解法：

                形如：y''+py'+qy=0(p,q为常数)叫做二阶常系数齐次线性微分方程。

        求通解的步骤：1.找到特征方程把：y''化成,y'化成,把y化成1。

                                2.判断得到的,是否相等来得到其对应的通解。

        二阶常系数非齐次线性微分方程及解法：

                  形如：y''+py'+qy=f(x)(p,q为常数)叫做二阶常系数非齐次线性微分方程。

        求通解的步骤：它的通解有点特殊的，是由两部分构成：第一部分：对应的二阶常系数齐次线性微分方程的通解，第二部分是二阶常系数非齐次线性微分方程的特解。它的特解根据不同情况需要具体再细分，我是会的哈哈哈哈，这里就不阐述了。