本文详细介绍了霍夫变换的基本原理和在OpenCV中的应用，包括直线和圆的检测。通过实例代码解析了如何使用Python和OpenCV进行直线检测，以及霍夫变换在圆检测中的实现。文章还探讨了参数设置对检测效果的影响，并展示了实际运行的图像结果。
序
认识世界能力不高，同行5分钟干完的活，你能干一天。所以是小白呐……
但是，一直白下去，和人的那种超越性是相悖的，所以，尝试超越一下吧，自我感动式超越。为什么是自我感动式？因为，我就那么点水平，只够自我感动的。
如何认识世界？按从低级到高级的顺序来试试吧。
百度，直观感受直线的检测
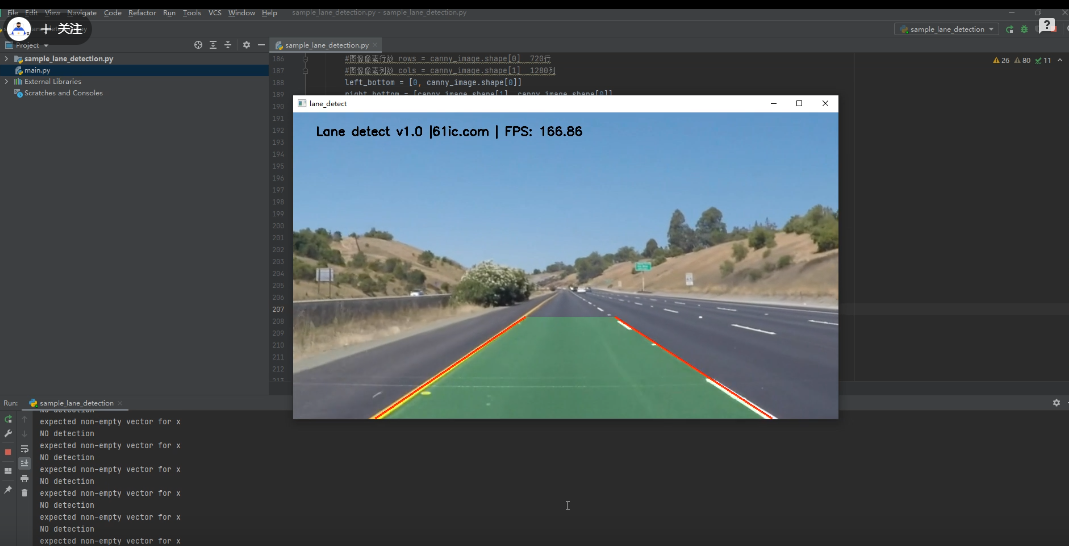
基于Python3.9+OpenCV4.5车道线及弯道检测_哔哩哔哩_bilibili
直线检测的原理
百度。小白除了百度，还能做什么呢……
网页1
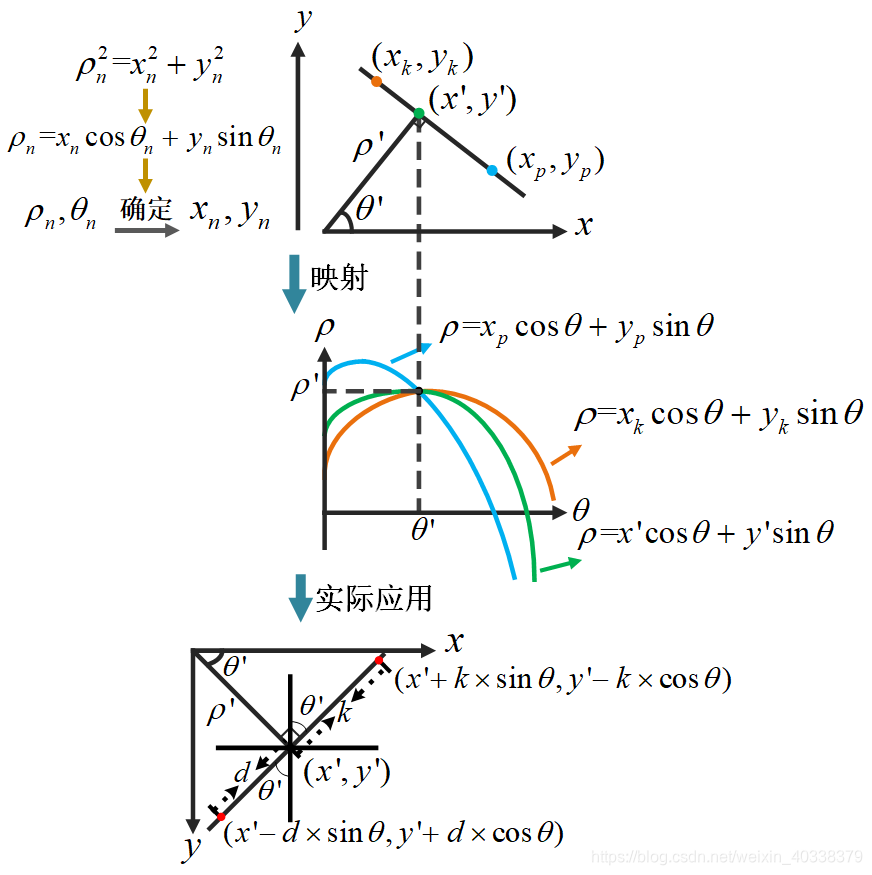
为了规避直线斜率不存在的情况，这里用极坐标【ρ，θ】来表示直线
如果空间中有3个点，如何判断这三个点在不在一个直线上，如果在，这条直线是的位置为？
这个例子中，对于每个点均求过该点的6条直线的【r，θ】坐标，共求了3*6个【r，θ】坐标。可以发现在θ=60时，三个点的r都近似为80.7，由此可判定这三个点都在直线【80.7，60】上。
通过 r-o-theta 坐标系可更直观表示这种关系，如下图：图中三个点的【r，θ】曲线汇集在一起，该交点就是同时经过这三个点的直线。引用自：
网页2
这个里面的，图很形象生动，也有代码
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread('room.jpg') gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#灰度图像 #open to see how to use: cv2.Canny #http://blog.youkuaiyun.com/on2way/article/details/46851451 edges = cv2.Canny(gray,50,200) plt.subplot(121),plt.imshow(edges,'gray') plt.xticks([]),plt.yticks([]) #hough transform lines = cv2.HoughLinesP(edges,1,np.pi/180,30,minLineLength=60,maxLineGap=10) lines1 = lines[:,0,:]#提取为二维 for x1,y1,x2,y2 in lines1[:]: cv2.line(img,(x1,y1),(x2,y2),(255,0,0),1) plt.subplot(122),plt.imshow(img,) plt.xticks([]),plt.yticks([])引用自：
(40条消息) Python下opencv使用笔记（十一）（详解hough变换检测直线与圆）_on2way的博客-优快云博客_cv2.houghlines
网页3
这个里面的，图很好看，也有代码
# -*- coding=GBK -*- import cv2 as cv import numpy as np def line_image(image): gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY) # 灰度图像 edges = cv.Canny(gray, 50, 200) lines = cv.HoughLinesP(edges, 1, np.pi/180, 30, minLineLength=60, maxLineGap=10) lines1 = lines[:, 0, :] # 提取为二维 for x1, y1, x2, y2 in lines1[:]: cv.line(image, (x1, y1), (x2, y2), (255, 0, 0), 1) cv.imshow("line", image) src = cv.imread("Line.png") cv.imshow("before", src) line_image(src) cv.waitKey(0) cv.destroyAllWindows()引用自：
(39条消息) python实现opencv学习十七：hough变换检测直线_云散月明晴的博客-优快云博客_hough变换直线检测python
网页4
这个里面，提了一下投票箱
引用：
网页5
这个也是，提了二维累加数组，累加器，Hough矩阵。
从直角坐标提到了极坐标。
引用自：
作为小白对这个原理的总结
百度了这么久，作为一个小白，看懂了什么？学会了什么？
所以，尝试写一写。
直线是由顶点组成的，点动成线，所以检测点也行。
它这个检测直线，大概就是，计算一下，是否有一条直线，能同时过RGB三个点。
怎么计算？把过RGB三个点的所有直线都画出来，看有没有一条直线是它们三个点公共的，有的话【比如下图里的ABCDEF直线】，ABC就共线。，这个直线就检测出来了。
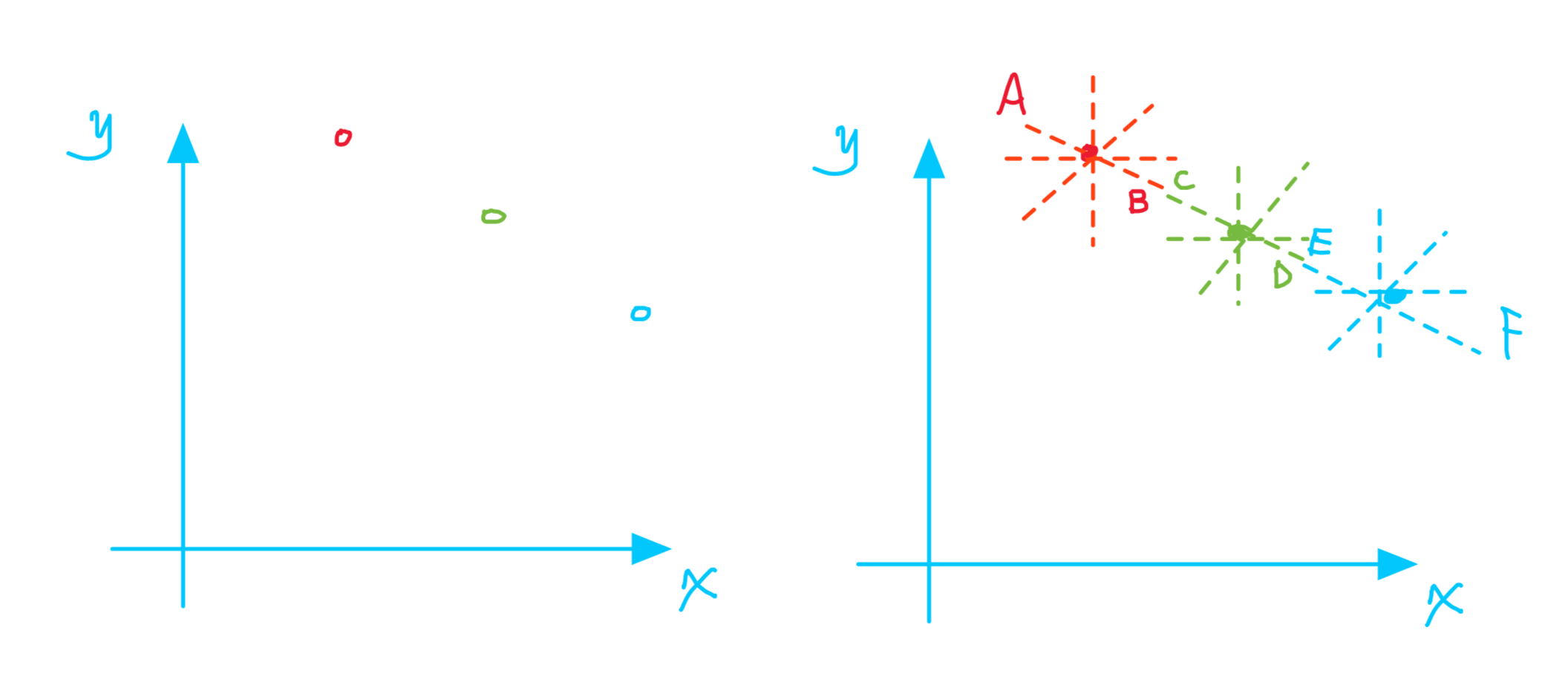
那末，如何表示过一个顶点的所有直线？
计算机不能直接处理自然语言，处理数学语言还差不多……
大概可以这么表示：
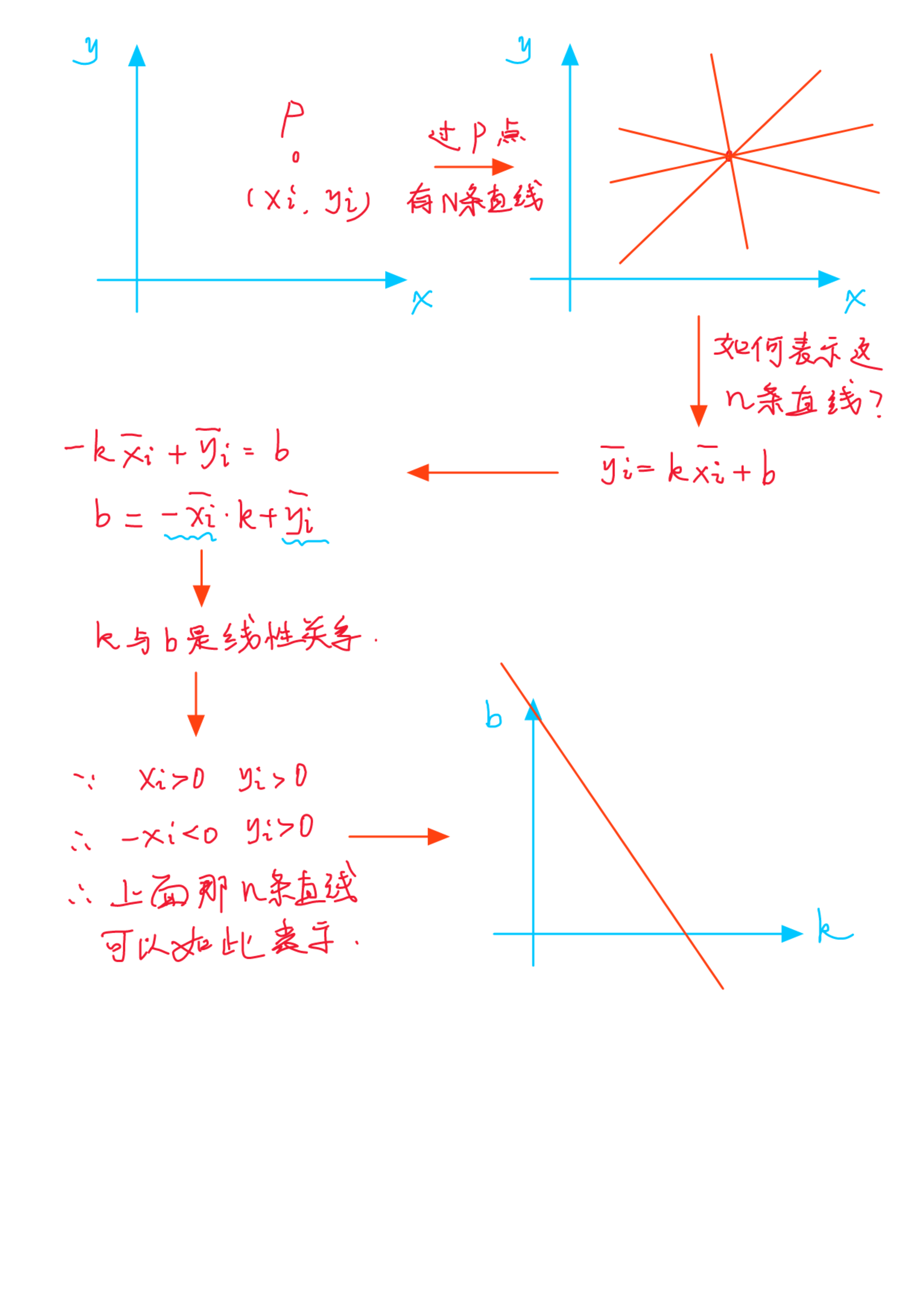
所以，过那3个点的，共3N条直线，就可以这么表示
那个交点，就表示上图的直线ABCDEF。
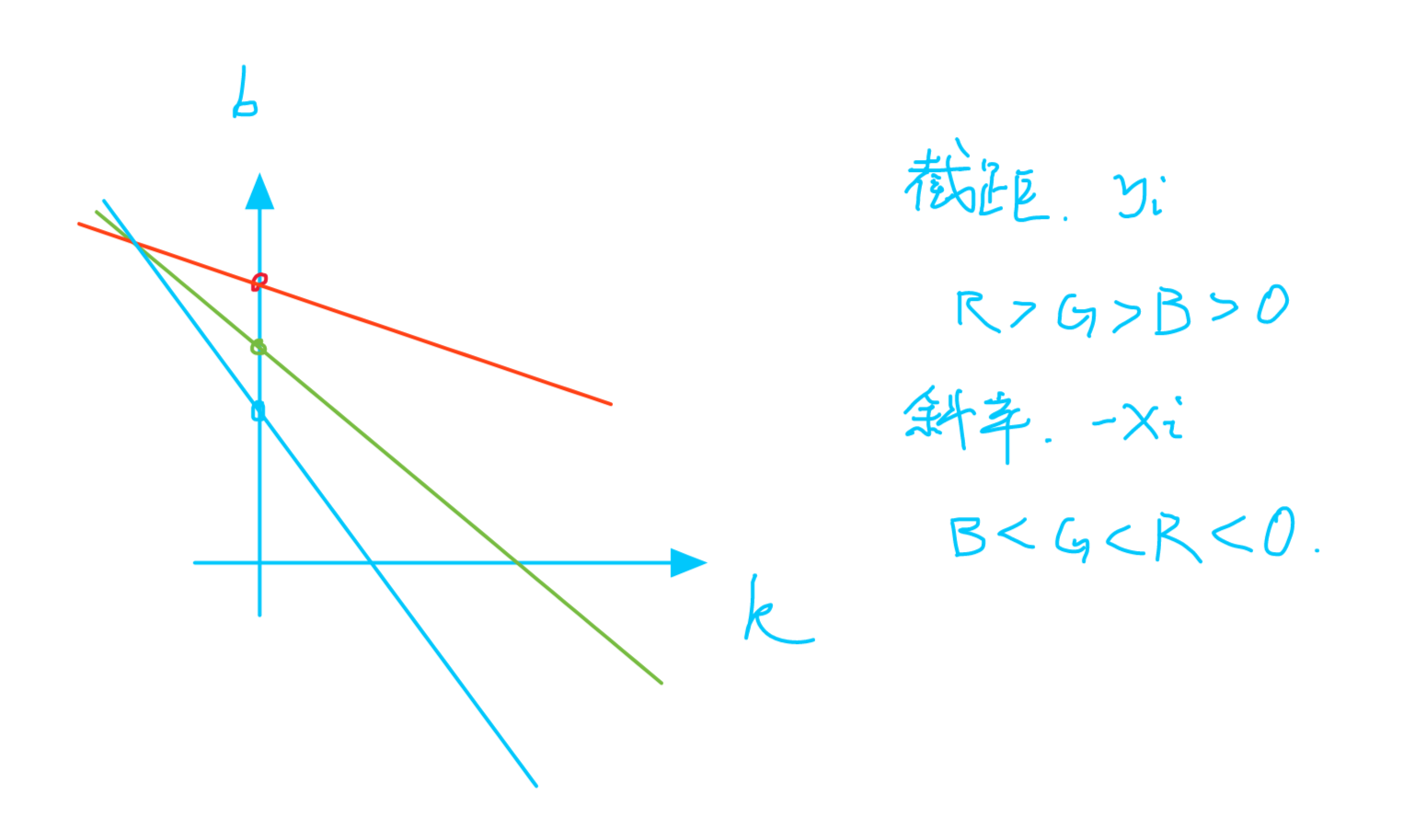
大概的原理，我理解的就是这样。
然后，为了规避斜率不存在的情况，把直线改成了极坐标来表示。
然后也是求交点，交点就代表直线。
没了。
直线检测的代码运行
作为一个小白，上面扯了这么多，实际应用才是真的啊，在哪里 ？怎么用？
首先，怎么配置环境？
这个链接里面:
(41条消息) Python如何安装OpenCV库_大表哥在曾母暗沙的博客-优快云博客_pythonopencv
说这样；
pip install opencv-python试试
好像可以了
复制代码，启动
从这里复制的代码：
(41条消息) Python下opencv使用笔记（十一）（详解hough变换检测直线与圆）_on2way的博客-优快云博客_cv2.houghlines
import cv2 as cv
import numpy as np
# hough变换检测直线与圆 ：https://blog.youkuaiyun.com/on2way/article/details/47028969
def line_image(image):
gray = cv.cvtColor(image, cv.COLOR_BGR2GRAY)#彩色信息对结果没有用，所以转化为灰度图，简化图片，减少计算量
edges = cv.Canny(gray, 50, 150, apertureSize=3) # 第四个输入参数是Sobel算子的大小，3的话就是3*3。这个算子，好像是提取边缘的。
cv.imshow("edges", edges)
lines = cv.HoughLines(edges, 1, np.pi / 180, 200) # 霍夫变换进行形状检测
# cv.HoughLines(edges, rho, theta, threshold)
# img 为输入的图像，Canny提取后的边界数据;rho/ρ为距离精确度（理解为距离单位）;theta/θ为角度精确度（理解为角度单位单位）;threshold 为累加器阈值,当累加器中的值高于threshold时才认为是一条直线
# 返回值每段直线(ρ,θ)的的二维矩阵
for line in lines:
rho, theta = line[0]
a = np.cos(theta) # np.cos是便于计算数组所有theta的cos值，sin同理 ，而且三角函数是np库里面的
b = np.sin(theta)
x0 = a * rho
y0 = b * rho
x1 = int(x0 + 1000 * (-b))
y1 = int(y0 + 1000 * (a))
x2 = int(x0 - 1000 * (-b))
y2 = int(y0 - 1000 * (a))
#将检测到的直线，绘制到图像上
cv.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2) # 输入参数： img， 起始点， 终， 颜色， 宽度
cv.imshow("line", image)
src = cv.imread("1.png")
cv.imshow("before", src)
line_image(src)
cv.waitKey(0)
cv.destroyAllWindows()原图——》边缘
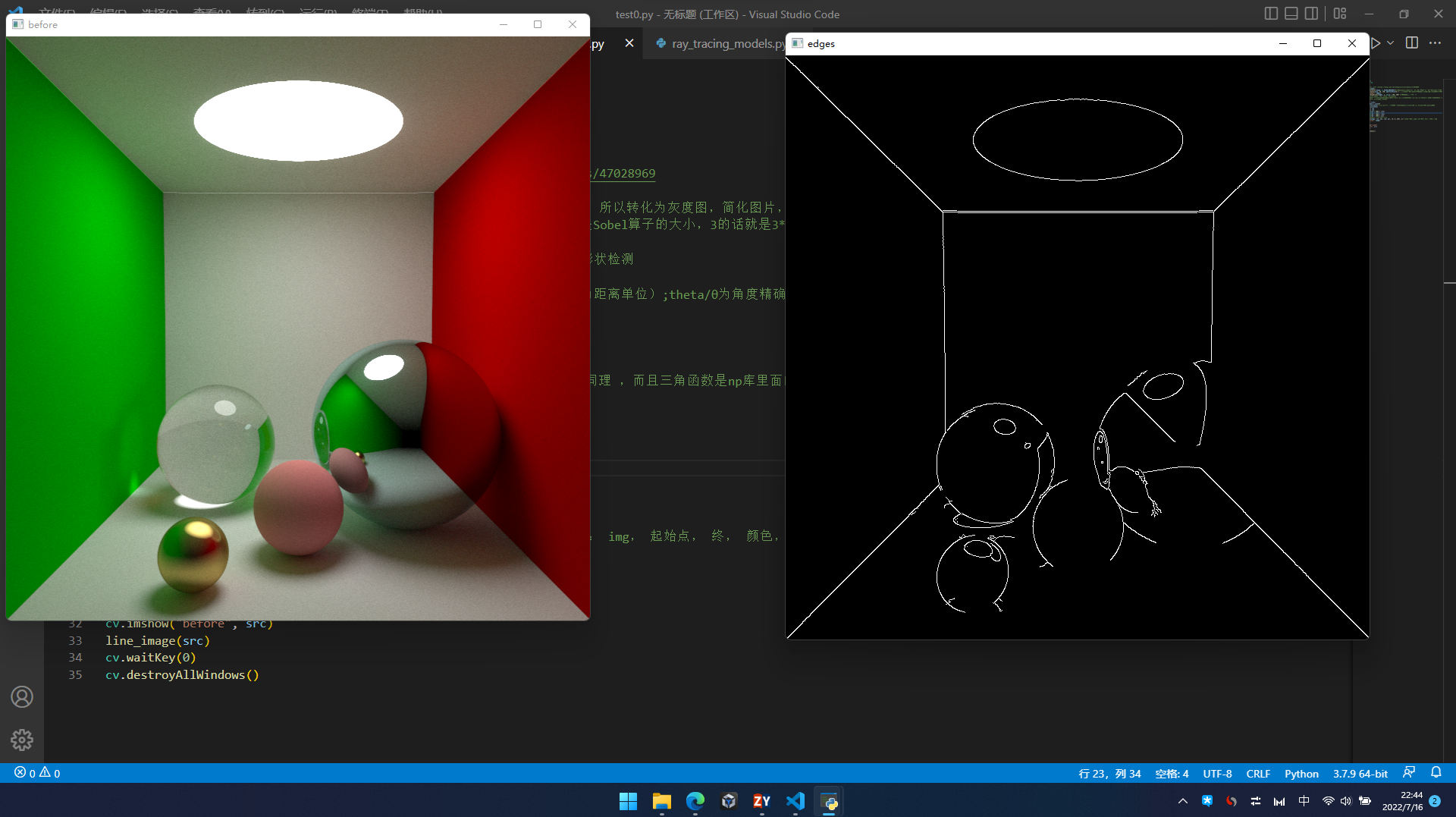
边缘——》直线
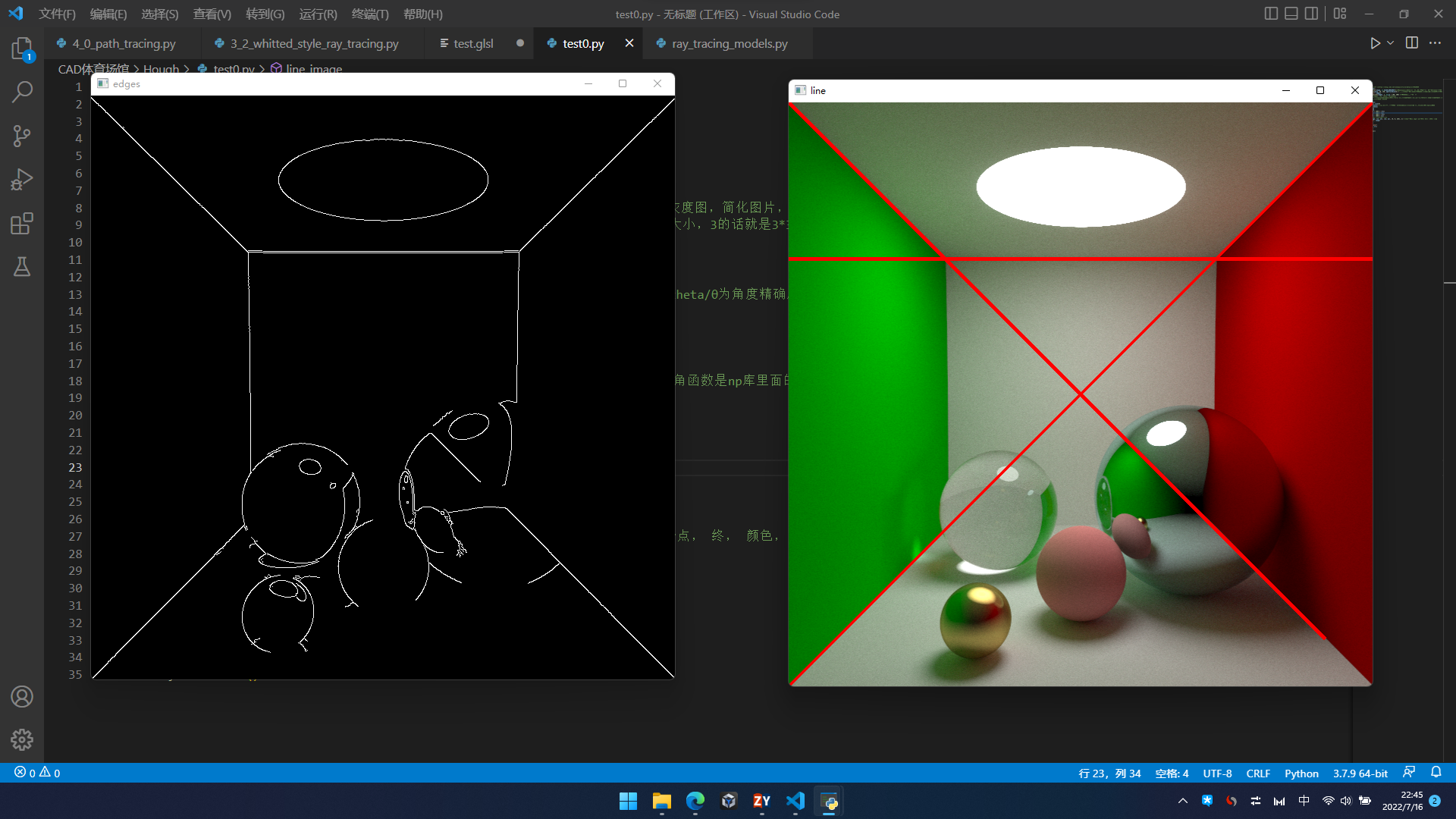这个直线。。标准的透视投影呐……也很合理，因为这个图就是按照路径追踪计算出来的……
但是，偶尔也会和理想偏离
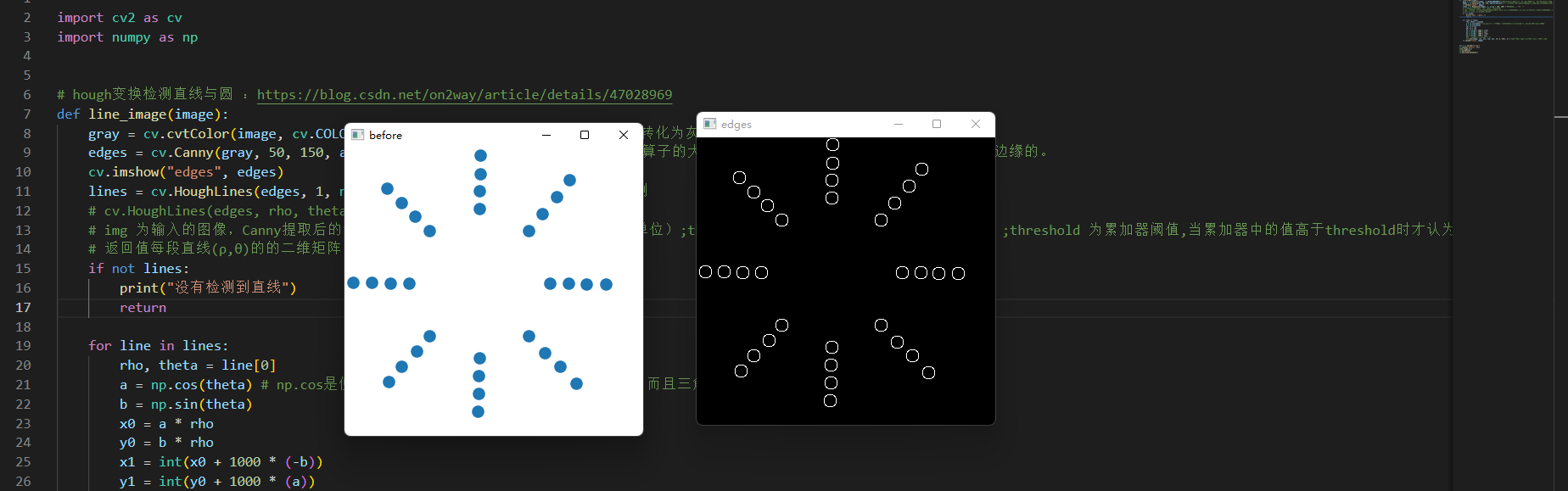
圆的检测的原理
大概和上面检测直线的差不多吧？
在平面直角坐标系中，圆的公式是：(x－a)²+(y－b)²=r²，有三个参数a、b、r，圆心坐标为（a，b），半径为r。
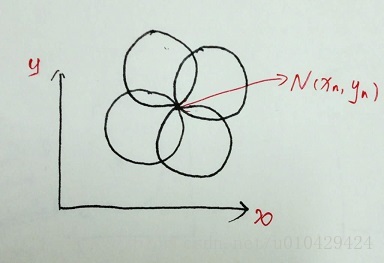
假设有一点N (xn, yn)，我们知道通过N的圆有无穷多个，比如下图中，我画出了4个通过N的圆。对于所有通过点N的圆来讲，势必满足公式：(xn－a)²+(yn－b)²=r²成立。其中，因为N是已知的，所以xn，yn是定值。而那些通过N的圆，有无穷多种，圆心、半径都是不一定的，所以a，b，r都是变量。
既然，a、b、r都是变量，我们可以用一个坐标系表示出a、b、r来，姑且叫它参数空间吧。那么，通过N点的所有圆，在这个参数空间中如何表示出来呢？首先来看：
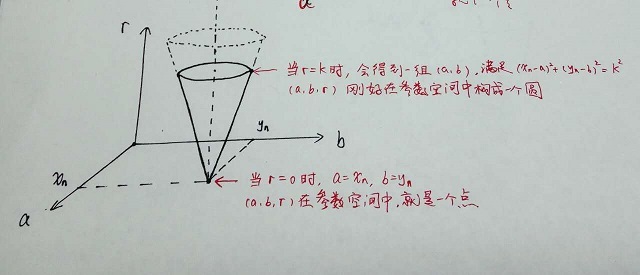
- 当r = 0时，根据公式(xn－a)²+(yn－b)²=r² ，能够计算出 a = xn，b = yn，此时（a、b、r）就是参数空间中的一个点。
- 当r = 1时，我们又能计算出一组(a、b)值，这些(a、b)值均满足公式(xn－a)²+(yn－b)²=r²，在参数空间中刚好构成一个圆。
- 同理，当r等于2、3、4、… ∞时，我们都能求出一组(a、b)值。把r从1到∞得到的所有的（a、b），在参数空间出画出来，就是一个圆锥面。
这只是仅有一个点N的情况，在参数空间中构成了一个圆锥面。
假设现在又有多了一个点M（xm，ym），在参数空间中又构成了另一个圆锥面。如果这两个圆锥面之间有一个交点P(ap, bp，rp)。说明点M、N共圆(ap、bp、rp)。论证如下：
- P(ap,bp,rp)在N构成的圆锥面上，则有(xn－ap)²+(yn－bp)²=rp²;
- P(ap,bp,rp)在M构成的圆锥面上，则有(xm－ap)²+(ym－bp)²=rp²;
- 根据上面两个公式可知，存在一个圆，它的圆心是(ap，bp)，半径是rp，圆上刚好有两个点N、M，满足该圆的方程：(x－ap)²+(y－bp)²=rp²。N（xn，yn）、M（xm，ym）刚好是这个方程的两个解。
当有多个点时，在参数空间中就会有多个圆锥面。多个圆锥面之间会有多个交点，只要我们找到那些交点，就能找到多个点之间的共圆。
hough变换的实质是坐标系的转换，将计算问题转化为计数问题，这是它最巧妙的地方。
引用自：
(41条消息) OpenCV自学笔记27. Hough变换：检测直线和圆_两鬓已不能斑白的博客-优快云博客_hough变换检测圆
圆的检测的代码实现
这个链接里有代码：
(41条消息) OpenCV自学笔记5：Hough变换检测直线和圆_两鬓已不能斑白的博客-优快云博客
那末，这个函数参数，都是什么意思？
cv2.HoughCircles的参数
圆形的表达式为(x−xcenter)2+(y−ycenter)2=r2(x−xcenter)2+(y−ycenter)2=r2，一个圆环的确定需要三个参数。那么霍夫变换的累加器必须是三维的，但是这样的计算效率很低。
这里opencv中使用霍夫梯度的方法，这里利用了边界的梯度信息。首先对图像进行canny边缘检测，对边缘中的每一个非0点，通过Sobel算法计算局部梯度。那么计算得到的梯度方向，实际上就是圆切线的法线。三条法线即可确定一个圆心，同理在累加器中对圆心通过的法线进行累加，就得到了圆环的判定。
cv2.HoughCircles函数的参数
cv2.HoughCircles(image, method, dp, minDist, circles, param1, param2, minRadius, maxRadius)
- image为输入图像，需要灰度图
- method为检测方法,常用CV_HOUGH_GRADIENT
- dp为检测内侧圆心的累加器图像的分辨率于输入图像之比的倒数，如dp=1，累加器和输入图像具有相同的分辨率，如果dp=2，累计器便有输入图像一半那么大的宽度和高度
- minDist表示两个圆之间圆心的最小距离
- param1有默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示传递给canny边缘检测算子的高阈值，而低阈值为高阈值的一半
- param2有默认值100，它是method设置的检测方法的对应的参数，对当前唯一的方法霍夫梯度法cv2.HOUGH_GRADIENT，它表示在检测阶段圆心的累加器阈值，它越小，就越可以检测到更多根本不存在的圆，而它越大的话，能通过检测的圆就更加接近完美的圆形了
- minRadius有默认值0，圆半径的最小值
- maxRadius有默认值0，圆半径的最大值
引用自：
返回值
通过百度，这个函数的返回值大概是这个意思：
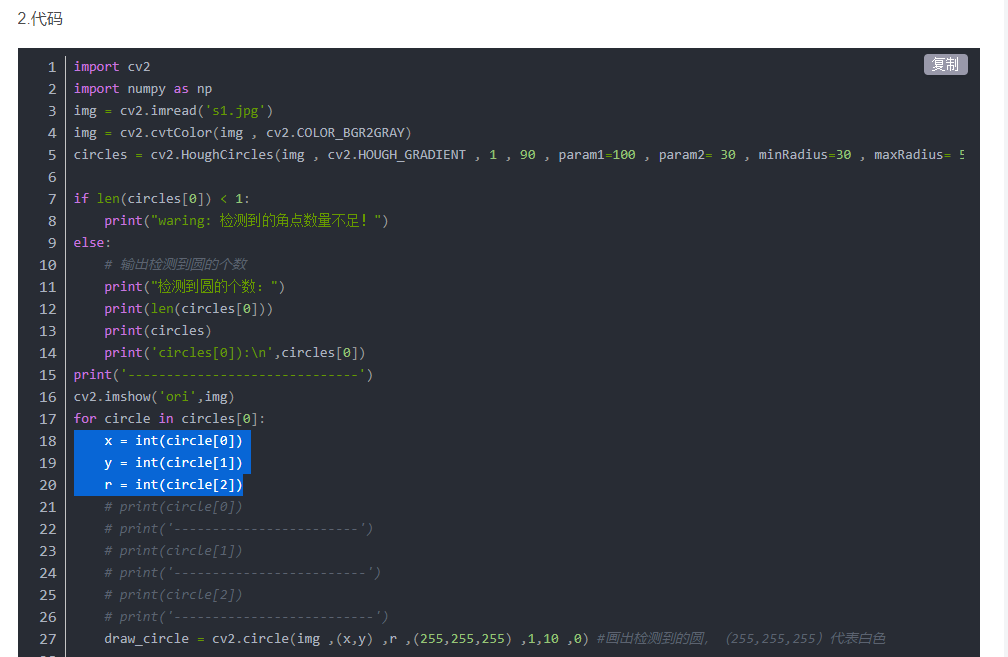引用自：
(41条消息) Python+opencv — cv2.HoughCircles（） 圆形检测，并顺时针给圆编序_不知名的小白66的博客-优快云博客_cv2.houghcircles
cv2.circle
大概是这个意思：
cv2.circle(img, center, radius, color[, thickness[, lineType[, shift]]])作用
根据给定的圆心和半径等画圆
参数说明
img：输入的图片data
center：圆心位置
radius：圆的半径
color：圆的颜色
thickness：圆形轮廓的粗细（如果为正）。负厚度表示要绘制实心圆。
lineType： 圆边界的类型。
shift：中心坐标和半径值中的小数位数。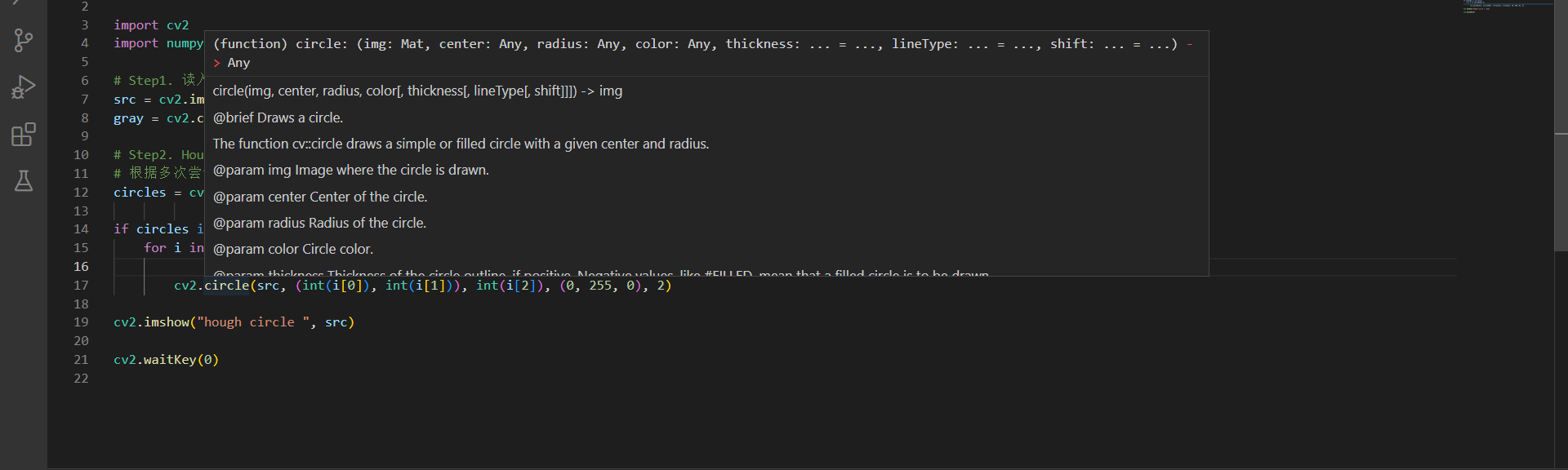
代码
# -*- coding:utf-8 -*-
import cv2
import numpy as np
# Step1. 读入图像
src = cv2.imread('2.jpg')
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
# Step2. Hough圆检测
# 根据多次尝试的结果，将param1调整为220时，检测效果较好
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, 1, 50,
param1=100, param2=10, minRadius=50, maxRadius=150)
if circles is not None:
for i in circles[0,:]:
cv2.circle(src, (i[0], i[1]), i[2], (0, 255, 0), 2)
cv2.imshow("hough circle ", src)
cv2.waitKey(0)
报错
小白，百度，启动
https://blog.youkuaiyun.com/weixin_44279924/article/details/121488230# -*- coding:utf-8 -*-
import cv2
import numpy as np
# Step1. 读入图像
src = cv2.imread('2.jpg')
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
# Step2. Hough圆检测
# 根据多次尝试的结果，将param1调整为220时，检测效果较好
circles = cv2.HoughCircles(gray, cv2.HOUGH_GRADIENT, dp=1, minDist=50,
param1=100, param2=10, minRadius=50, maxRadius=100)
if circles is not None:
for i in circles[0,:]:
cv2.circle(src, (int(i[0]), int(i[1])), int(i[2]), (0, 255, 0), 2)
cv2.imshow("hough circle ", src)
cv2.waitKey(0)
结果
输入的图像
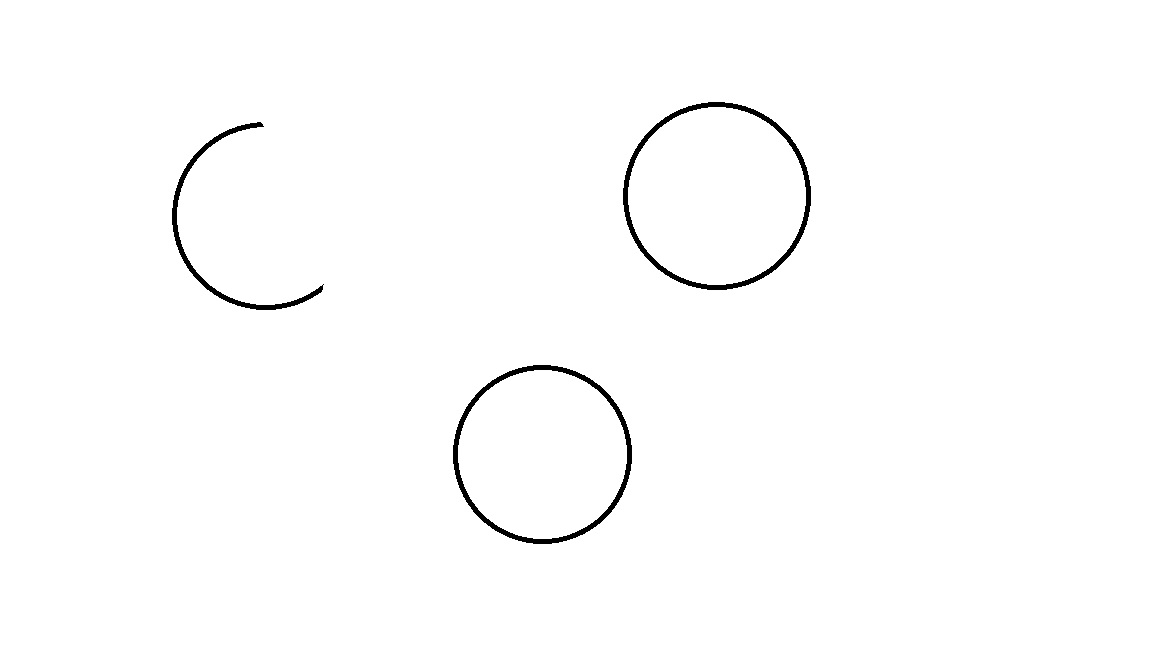
输出的图像
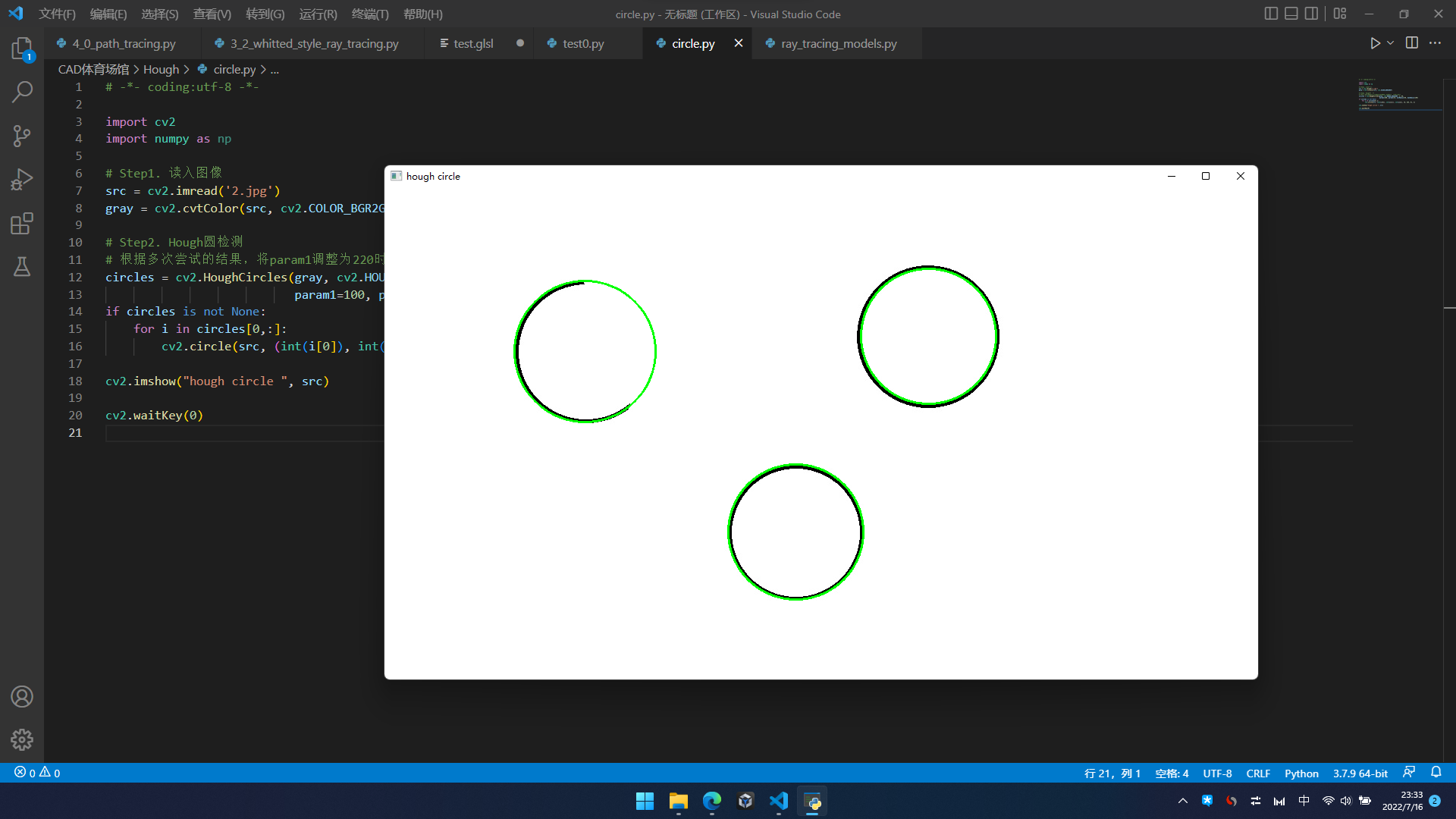输入的图像
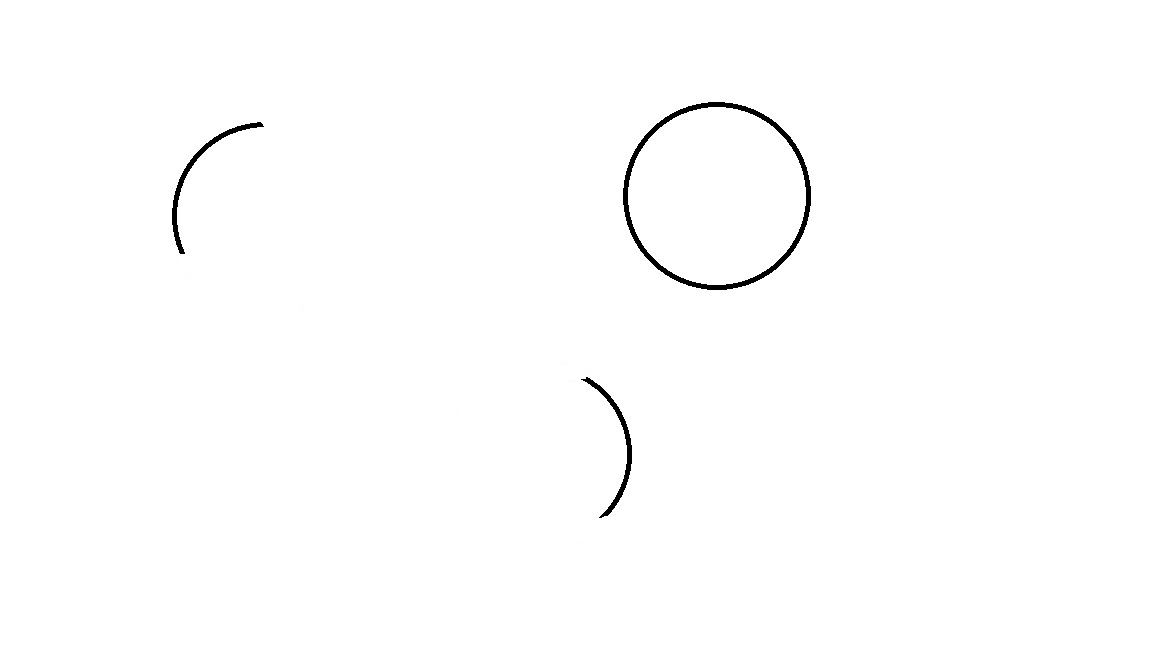
输出的图像
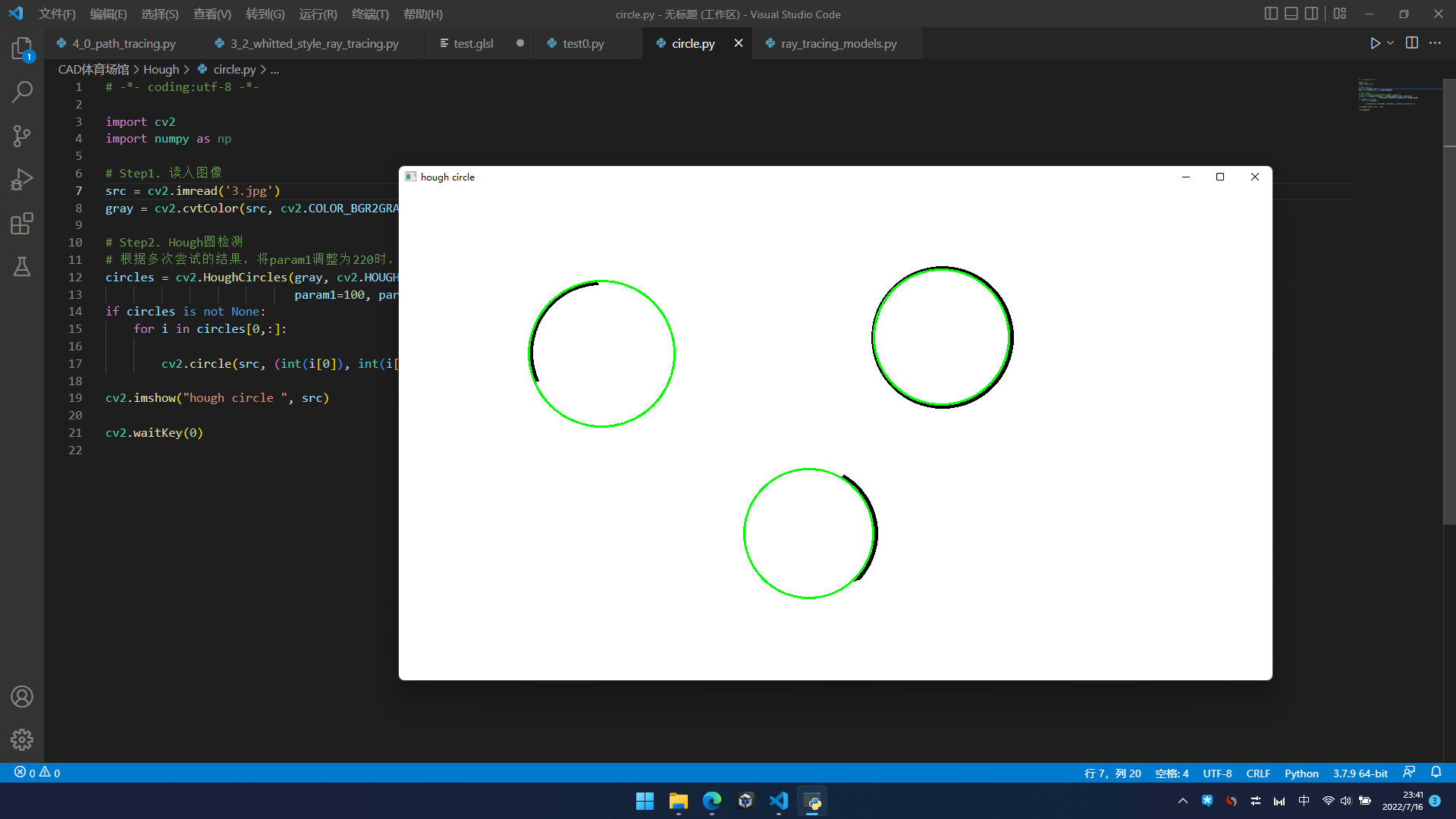
也行。。。。
敢于调参的话，也能调出这种效果：
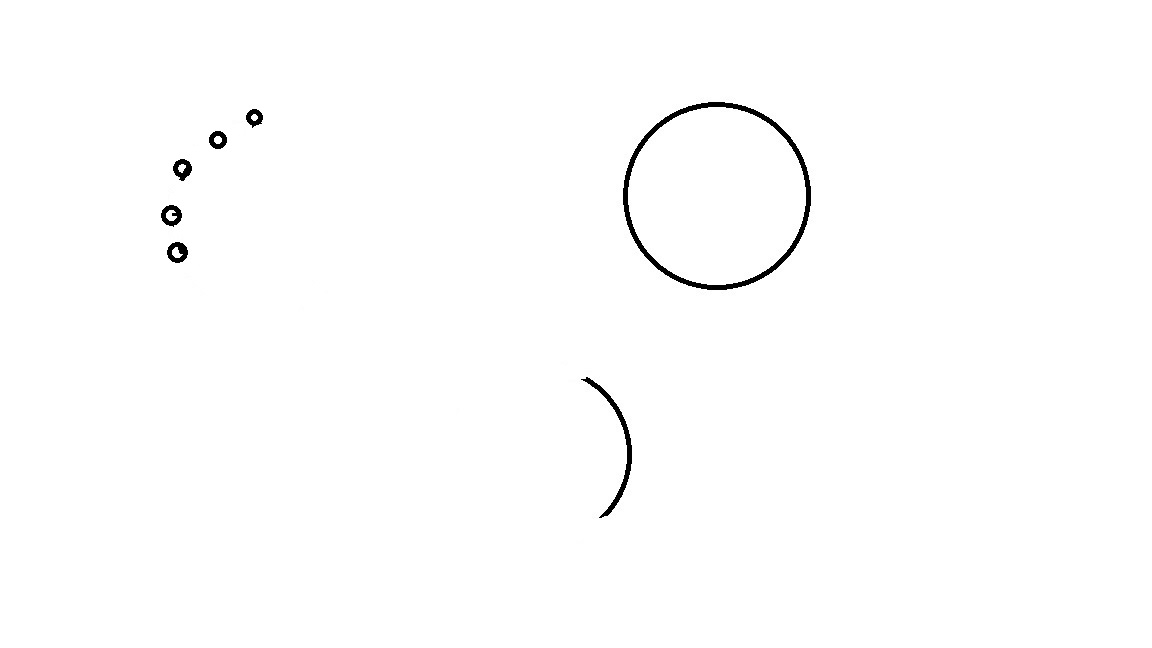
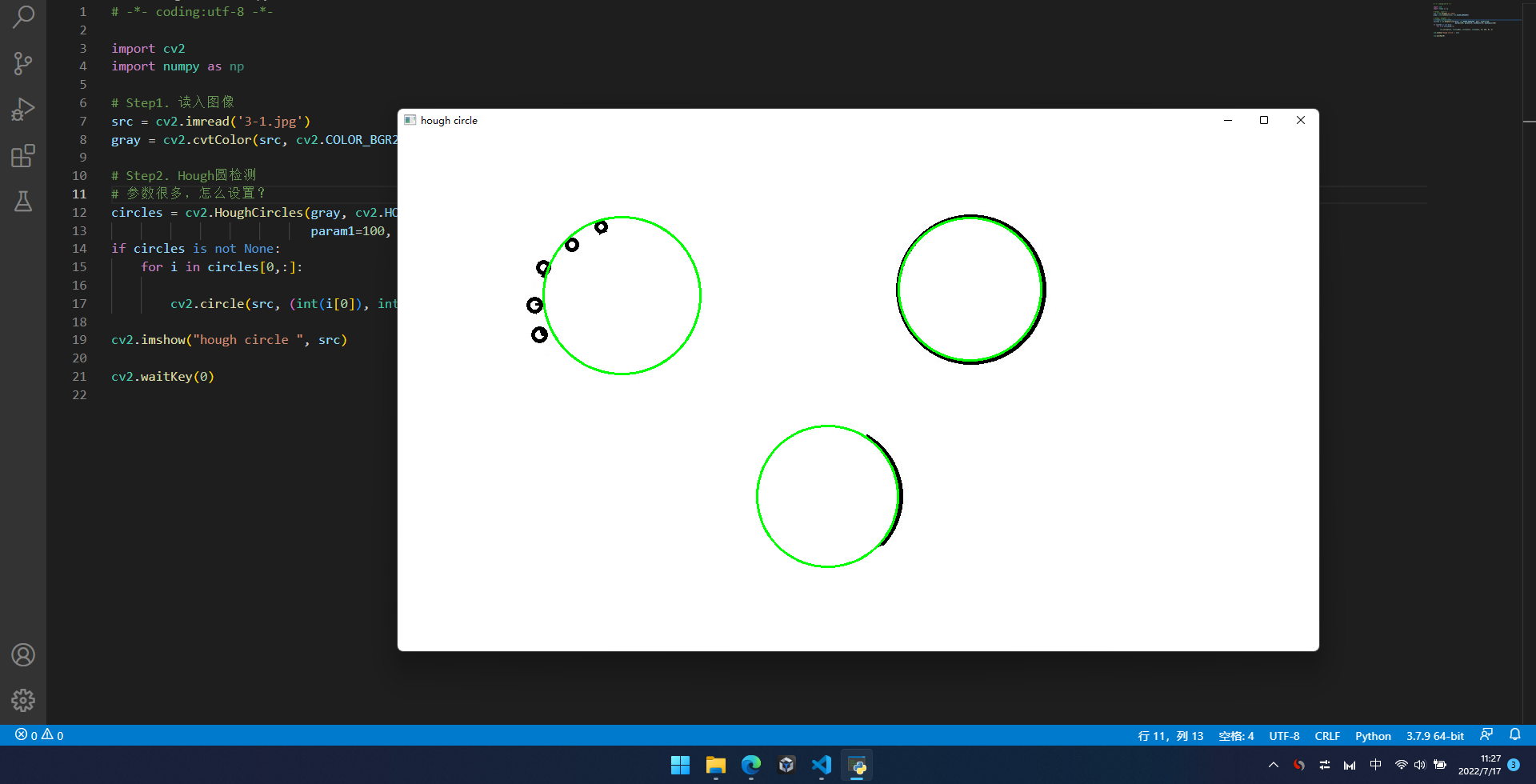
后记
上面写的对吗？不知道，小白而已。写出来就已经是极限了，哪里管什么对错？
扫一扫
1907
到【灌水乐园】发言
