Fibonacci数列
无穷数列1,1,2,3,5,8,13,21,34,55,……,称为Fibonacci数列。它可以递归地定义为:
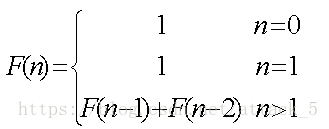
第n个Fibonacci数可递归地计算如下:
int fibonacci(int n)
{
if (n <= 1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
- 编写完整的主函数,分别记录利用上述递归函数求第45,46,47,48个Fibonacci数所花费的时间。
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
int fibonacci(int n)
{
if(n<=1)return 1;
return fibonacci(n-1)+fibonacci(n-2);
}
void main()
{
double a,b,c,d;
a=clock() / CLOCKS_PER_SEC;
fibonacci(45);
a=clock() / CLOCKS_PER_SEC-a;
printf("求第45个Fibonacci数所花时间:%f\n",a);
b=clock() / CLOCKS_PER_SEC;
fibonacci(46);
b=clock() / CLOCKS_PER_SEC-b;
printf("求第46个Fibonacci数所花时间:%f\n",b);
c=clock() / CLOCKS_PER_SEC;
fibonacci(47);
c=clock() / CLOCKS_PER_SEC-c;
printf("求第47个Fibonacci数所花时间:%f\n",c);
d=clock() / CLOCKS_PER_SEC;
fibonacci(48);
d=clock() / CLOCKS_PER_SEC-d;
printf("求第48个Fibonacci数所花时间:%f\n",d);
}
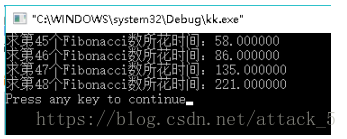




 本文详细介绍了Fibonacci数列的递归计算方法,并通过实验记录了计算第45至48个数的时间消耗,揭示了递归算法在处理大量数据时的性能瓶颈。
本文详细介绍了Fibonacci数列的递归计算方法,并通过实验记录了计算第45至48个数的时间消耗,揭示了递归算法在处理大量数据时的性能瓶颈。
















 8502
8502

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








