数理统计的基础概念
简单随机样本
定义:设总体 X 是一个具有分布函数 F(x) 的随机变量,若随机变量 X1, X2, ..., Xn 满足:
- 独立性:X1, X2,..., Xn 相互独立;
- 同分布性:每个 Xi 都与总体 X 同分布,即
。
则称 X1, X2, ..., Xn 为来自总体 X 的容量为 n 的简单随机样本(样本)。
对样本的一次观测值 x1, x2, ..., xn 称为样本值。
统计量
定义:设 X1, X2, ..., Xn 是来自总体 X 的一个样本,g(X1, X2, ..., Xn) 是样本的不含未知参数的连续函数,则称 g(X1, X2, ..., Xn) 为一个统计量。
常用统计量
| 统计量名称 | 公式 | 作用 |
|---|---|---|
| 样本均值 | 估计总体均值 E(X) | |
| 样本方差 | 估计总体方差 D(X) (n-1为自由度) |
补充性质:
- 若总体
,则
三大统计分布
1. 分布
定义:设 X1, X2, ..., Xn 相互独立,且都服从标准正态分布 N(0, 1),则称随机变量
服从自由度为 n 的 分布,记为
。
性质:
- 可加性:若
,且 X 与 Y 独立,则
;
- 数字特征:
;
- 上α分位点:满足
的点
称为上α分位点。
2. 分布
定义:设 ,且 X 与 Y 相互独立,则称随机变量
服从自由度为 n 的 t 分布,记为 。
若 ,则
。
性质:
- 对称性:t 分布的概率密度函数关于 t = 0 对称,与标准正态分布形状类似;
- 数字特征:
;
- 上α分位点:满足
的点
称为上α分位点,且
3. 分布
定义:设 ,且 X 与 Y 相互独立,则称随机变量
服从第一自由度为 n1,第二自由度为 n2 的 F 分布,记为 。
性质:
- 倒数性质:若
,则
;
- 数字特征:
;
- 上α分位点:满足
的点
称为上α分位点。
例题:
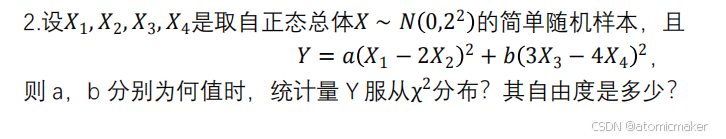
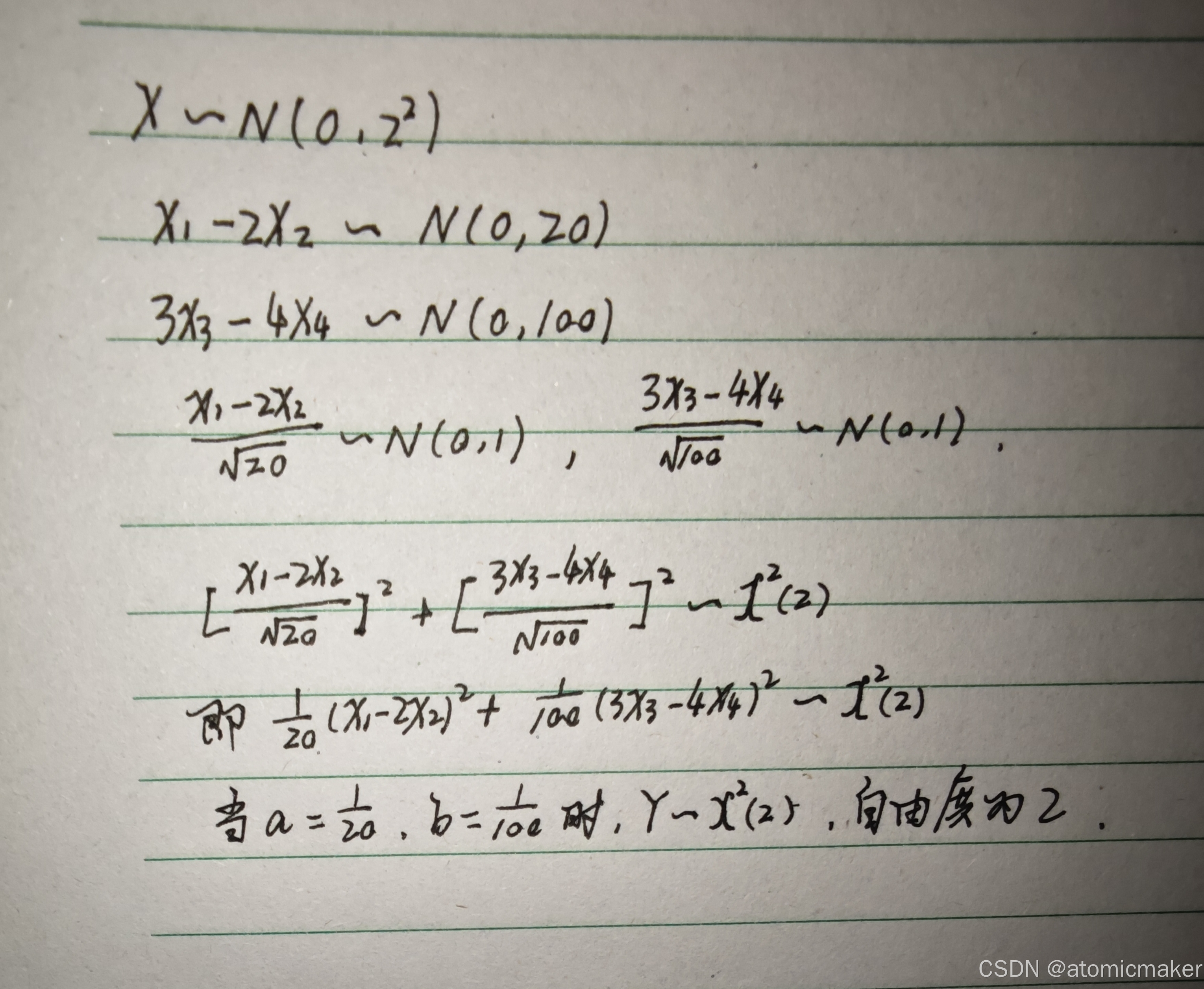
单正态总体的抽样分布
设总体 ,X1, X2, ..., Xn 是来自 X 的样本,
样本均值 ;样本方差
| 统计量 | 分布结论 | 适用条件 |
|---|---|---|
| 样本均值分布 | ||
| 样本方差分布 | ||
| 均值的 t 分布 |
双正态总体的抽样分布
设总体 ,X1, ..., Xn1 是来自 X 的样本,Y1, ..., Yn2 是来自 Y 的样本,且两样本相互独立。记
1.均值差的分布
1) 均已知
2) 但未知
其中 称为合并方差。
2.方差比的分布
参数估计
估计量的无偏性与有效性
设总体 X 的未知参数为 θ, 是 θ 的一个估计量。
1.无偏性
若估计量 的数学期望等于未知参数
,即
。
判别:
- 样本均值
是总体均值
的无偏估计;
- 样本方差
是总体方差
的无偏估计。
2.有效性
设 和
都是
的无偏估计量,若对任意样本容量 n,有
则称 比
更有效。
即在无偏的前提下,方差越小的估计量,取值越集中于真实参数 θ 附近,估计精度越高。
例题:


矩估计法与极大似然估计法
1.矩估计法
基本思想:用样本矩替换总体矩,用样本矩的函数替换总体矩的函数。
题目中表示用样本均值 去替换总体均值
。
2.极大似然估计法
基本思想:
离散型和连续型步骤是一样的,只是求似然函数的方法不一样。
设离散型总体分布律为 ,连续型总体概率密度为
,θ 为未知参数。
注意: 表示连乘。
- 写出似然函数:
(离散型),
(连续型)
- 取对数得到对数似然函数(简化计算):
,
- 求对数似然函数的最大值点(对 θ 求导并令导数为 0):
:
- 解方程得
的极大似然估计值
,对应估计量。
离散型:
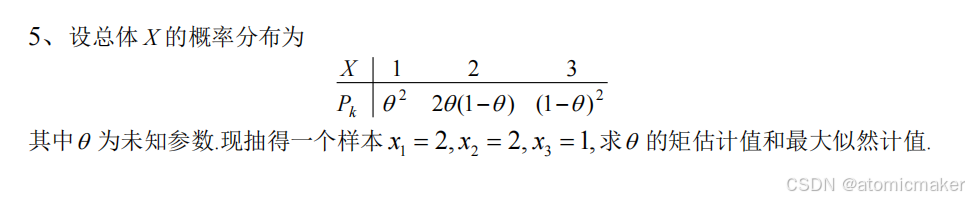
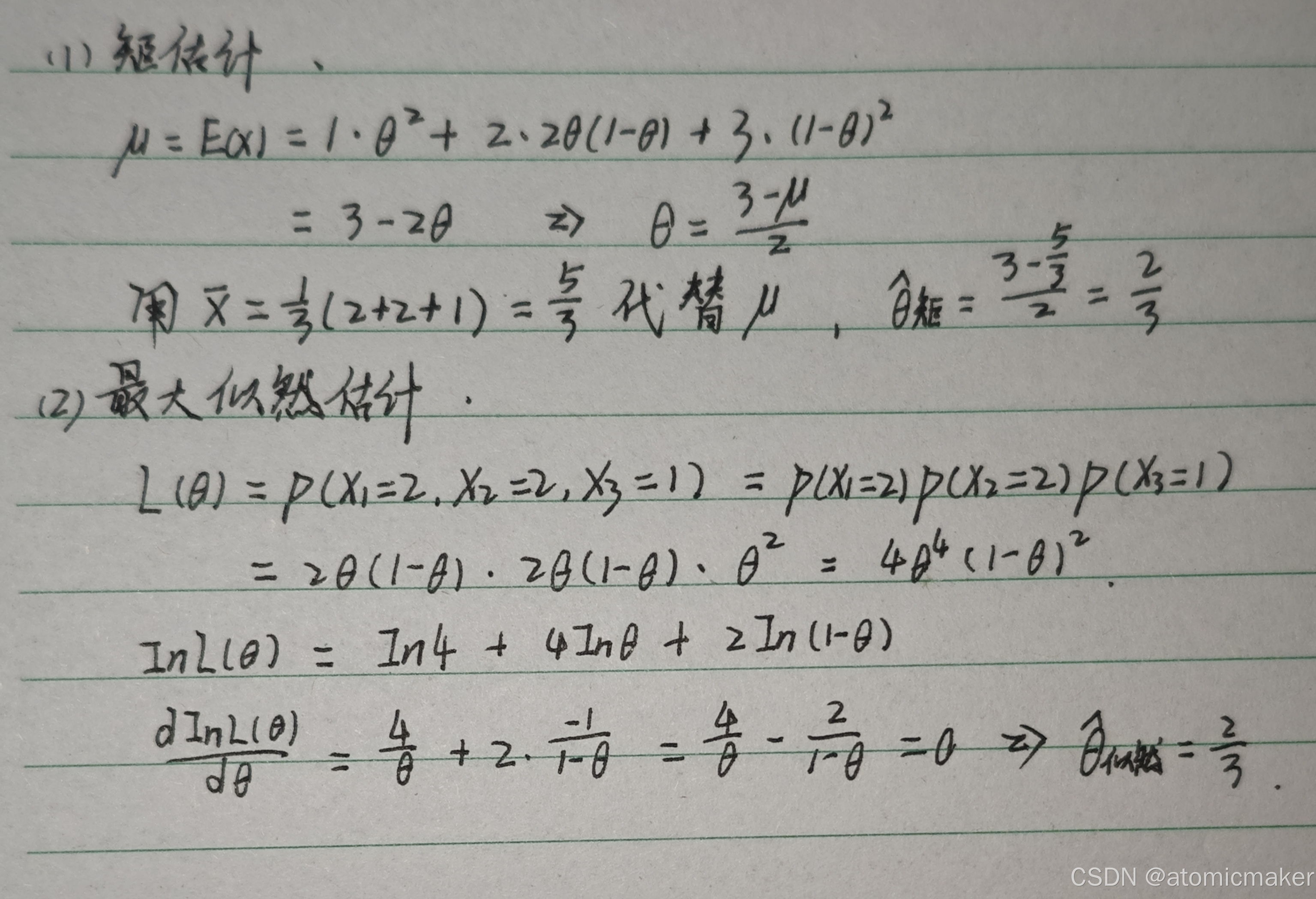
连续型:
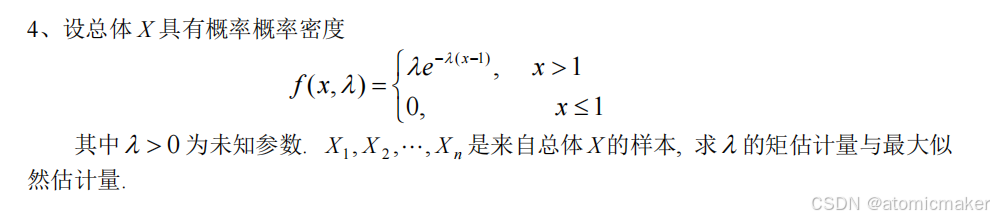
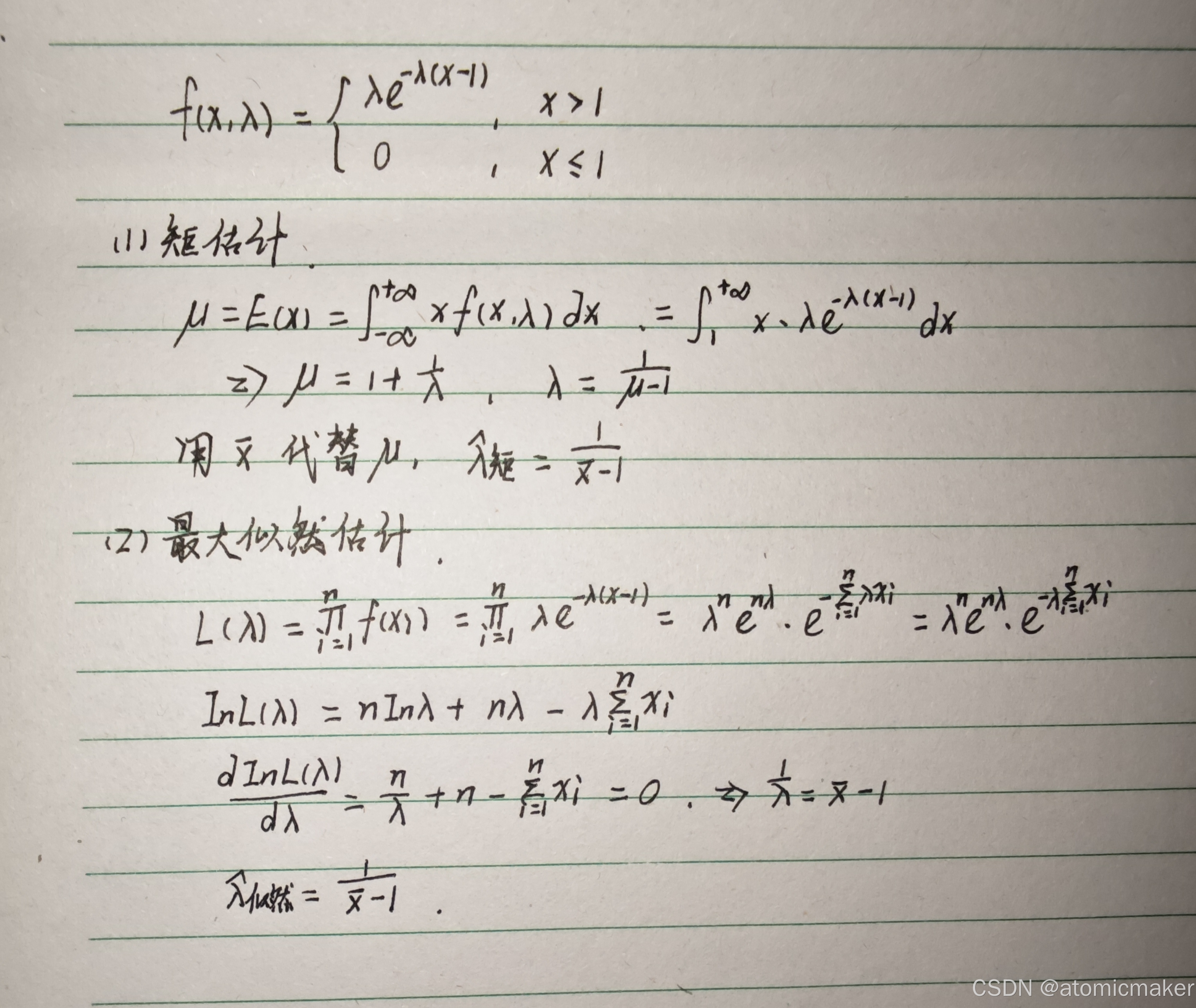
单正态总体的置信区间
设总体,X1, X2, ..., Xn 是样本,
样本均值 ;样本方差
;置信水平
。
1.均值的置信区间()
1) 已知
推导依据:
标准正态分布的对称性,
的置信区间:
2) 未知
推导依据:
分布的对称性,
的置信区间:
2.方差的置信区间()
1) 已知/未知
推导依据:
分布非对称,取上 α/2 分位点
和上 1-α/2 分位点
,满足
的置信区间:
例题:


假设检验
假设检验的两类错误
假设检验中,由于样本的随机性,决策结果可能出现两类错误,且两类错误无法同时避免,降低一类错误概率会导致另一类错误概率上升(样本量固定时)。
| 错误类型 | 定义 |
|---|---|
| 第一类错误(弃真错误) | 原假设 |
| 第二类错误(取伪错误) | 原假设 |
假设检验的基本步骤
1.建立假设
- 零假设 H0:需要被检验的假设(如:
);
- 对立假设 H1:与 H0 相反的假设,分为双侧(
)和单侧(
)
2.构造检验统计量
根据总体分布、参数是否一致,选择合适的统计量,要求:
- 统计量是样本的函数,不含未知参数;
- H0 为真时,统计量的分布已知(如
)。
3.确定拒绝域
- 根据显著性水平 α 和 H1 的类型(双侧 / 单侧),查分布表得到临界值;
- 拒绝域:使 H0 被拒绝的统计量取值范围,双侧检验拒绝域在分布两侧,单侧检验在一侧。
4.计算检验统计量的观测值
代入样本数据,计算检验统计量的具体数值。
5.做出决策
- 若统计量观测值落在拒绝域内,则拒绝 H0,接受 H1;
- 若统计量观测值未落在拒绝域内,则不拒绝 H0。
单正态总体的假设检验
1.检验均值
检验
1) 已知
构造检验统计量
2) 未知
构造检验统计量
2.检验方差
构造检验统计量
例题:



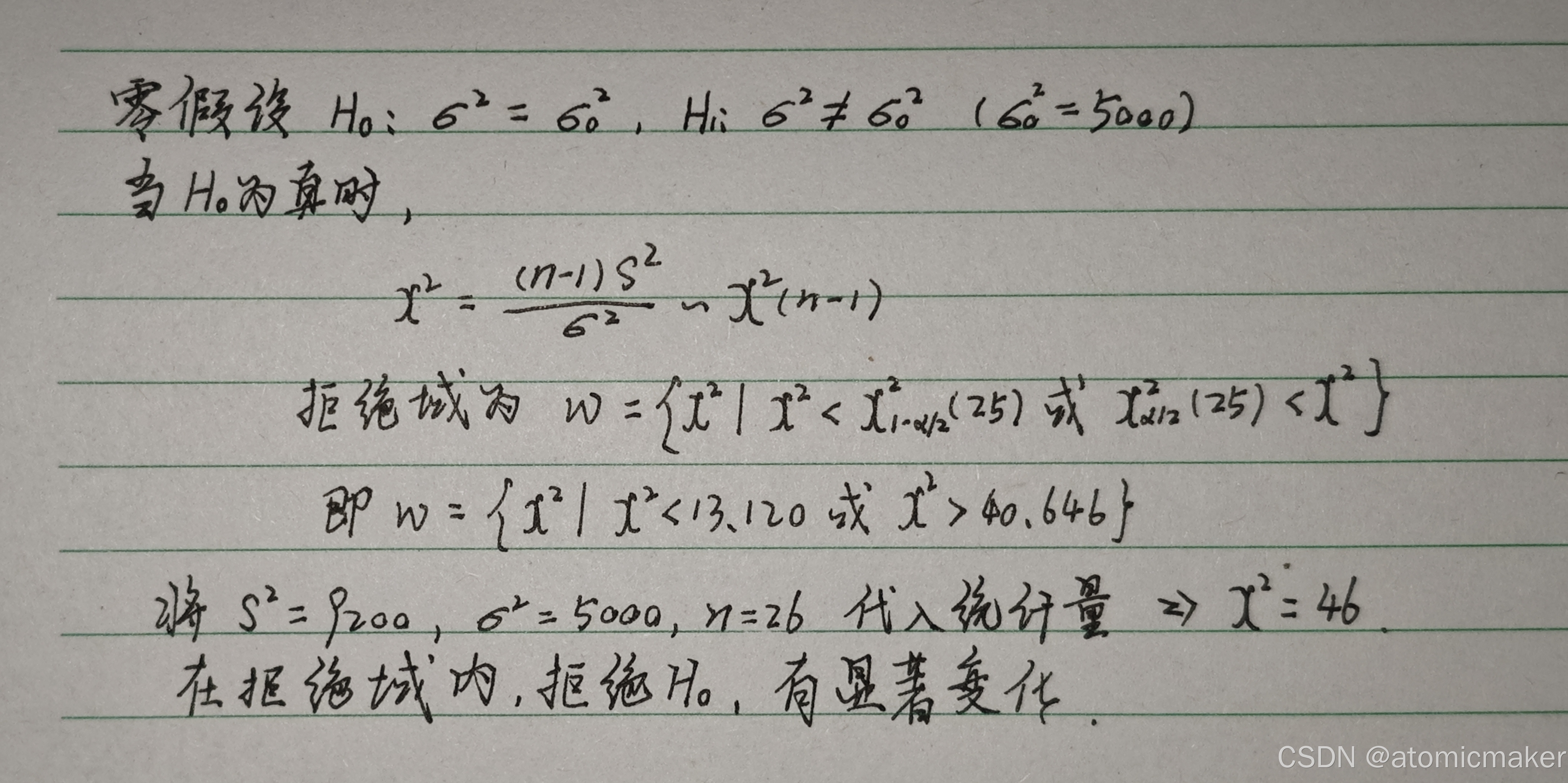




















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








