设有6种不同面值的硬币,各硬币的面值分别为5分、1角、2角、5角、1元和2元。现在要用这些面值的硬币来购物和找钱。购物时可以使用的各种面值的硬币个数存于数组Coins[1:6]中,假设商店里各面值的硬币有足够多。对于给定的付款金额,计算使用硬币个数最少的交易方案。
输入数据的每一行有6个整数和一个有2位小数的实数,
分别表示可以使用的各种面值的硬币个数和付款金额。
输出为交易所需要的最少硬币个数,如果不可能完成交易,则输出“impossible”。
问题解释:
这里要注意一个点:
此处交易所需的最少硬币个数为 你支付的硬币个数 + 商店找给你的硬币个数。
例如:
一次购物需要支付0.95元,你可以给他的硬币组合为: 0.5 一个 + 0.2 两个 + 0.05 一个
0.5+0.2+.0.2+0.05=0.95
即 此处使用了四个硬币完成了交易。但我们发现,如果我们支付 一个 1 元的硬币,商店找回给我们一个0.05的硬币,仅需要两个硬币便完成的交易。
1-0.05=0.95
贪心算法:
所谓贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性。
贪心算法的基本思想:
解决本问题的关键在于找到贪心变量,本问题的贪心变量为实际支付金额。由于改变了支付面额的大小,以及商店会找零,就是对于这些硬币的排列组合。
步骤:
遍历备选的元素
选择贪心策略
I中剩余元素不发生变化,
I剩余元素不会变化。
接下来就是代码了,请自行观看:
def contains(a):
for i in range(0,6):
if (coinvalue[i] == a and coins[i] > 0):
return i
return -1
def greed(coinvalue,changvalue,coins,Pay):
global coinnum
for i in range(5, -1, -1):
#从大到小遍历
if coins[i] > 0:
#如果顾客手里有剩余硬币
for j in range(i):
#商店的硬币从小到大遍历,进行找零
realmoney = coinvalue[i] - changvalue[j]
#实际上的支付金额=支付硬币的价值-商店找零的价值
if Pay >= realmoney:
#只有当实际支付金额效玉目标金额时才进行选取,否则需要增加找零硬币的金额(即,继续本层循环 j)
if coins[i] >= Pay // realmoney:
#如果当前面值硬币找零后足够支付余额
tempcoinnum = Pay // realmoney
coinnum += tempcoinnum * 2
#如果顾客有该硬币,则无需找零,因为找零会消耗两个硬币。
if(contains(realmoney) != -1):
tempcoinnum = min(tempcoinnum, coins[contains(realmoney)])
coinnum -= tempcoinnum
coins[contains(realmoney)] -= tempcoinnum
else:
coins[i] -= Pay // realmoney
Pay = Pay % realmoney
if (contains(coinvalue[i]) == -1):
break
else:
coinnum += coins[i]
Pay = Pay - coinvalue[i] * coins[i]
coins[i] = 0
def outoutresult():
if coinnum == 0 or Pay == 0:
print("imossible !")
else:
print("支付和找零需要的最少总硬币数量:",coinnum)
coinnum = 0
coinvalue = [5, 10, 20, 50, 100, 200]
changvalue = [0, 5, 10, 20, 50, 100, 200]
realmoney = 0
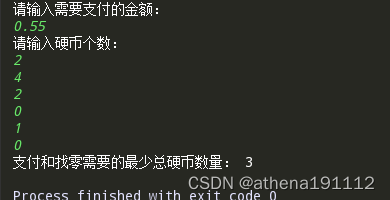
print("请输入需要支付的金额:")
costt = float(input())
Pay = int(costt * 100)
coins = []
print("请输入硬币个数:")
for i in range(0,6):
coins.append(int(input()))
greed(coinvalue,changvalue,coins ,Pay)
outoutresult()









 本文介绍如何利用贪心算法解决实际支付和找零问题,通过调整支付面额和考虑商店找零,确定使用最少硬币完成交易。通过实例演示了如何遍历硬币面值并选择最优组合,适用于货币支付场景。
本文介绍如何利用贪心算法解决实际支付和找零问题,通过调整支付面额和考虑商店找零,确定使用最少硬币完成交易。通过实例演示了如何遍历硬币面值并选择最优组合,适用于货币支付场景。
















 2694
2694

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








