异质三维集成电路噪声耦合分析

5 异质三维集成电路中的衬底噪声耦合

本章提纲

5.1 异质衬底耦合.120
5.1.1 常见电路与兼容衬底类型.120
5.1.2 不同衬底材料的电阻特性.121
5.1.3 不同衬底材料的噪声模型简化.121
5.2 频率响应.124
5.2.1 噪声耦合系统的隔离效率.124
5.2.2 噪声耦合系统的传递函数.124
5.3 提高噪声隔离的技术.127
5.3.1 地下网络电感.127
5.3.2 攻击者与受害者之间的距离.128
5.4 总结.135

噪声耦合在集成电路设计过程中日益重要 [244]。该主题也是三维（3‐D）电路中的一个基本问题，其中信号通过硅通孔（TSVs）分布在多个不同的层之间，从而在3‐D系统内形成一种电子风暴。多种类型的信号（电源、时钟和数据）可以在这些垂直互连中传播。在3‐D集成中采用了多种TSV工艺，包括先通孔、中通孔和后通孔 [245] （参见第3章，三维集成电路制造技术）。在这些工艺中，硅通孔位于某一层的衬底内部，并与该层的金属互连相连。这些硅通孔大大缓解了全局信号问题。然而，它们也带来了新的障碍；具体而言，即通过硅通孔向各层衬底中的噪声耦合。该噪声通过衬底传播，并影响靠近硅通孔的受害电路。本章旨在描述由不同衬底材料构成的异质3‐D系统中的耦合噪声。从硅通孔到异质衬底的噪声耦合机制，以及不同衬底的特性与应用，在第5.1节中进行了总结。在频域中表征噪声耦合系统的耦合噪声及相关传输函数在第5.2节中讨论。一些增强噪声隔离的技术在第5.3节中提出。最后，第5.4节给出了总结。

鲍里斯·瓦斯班德先生为本章做出了贡献。

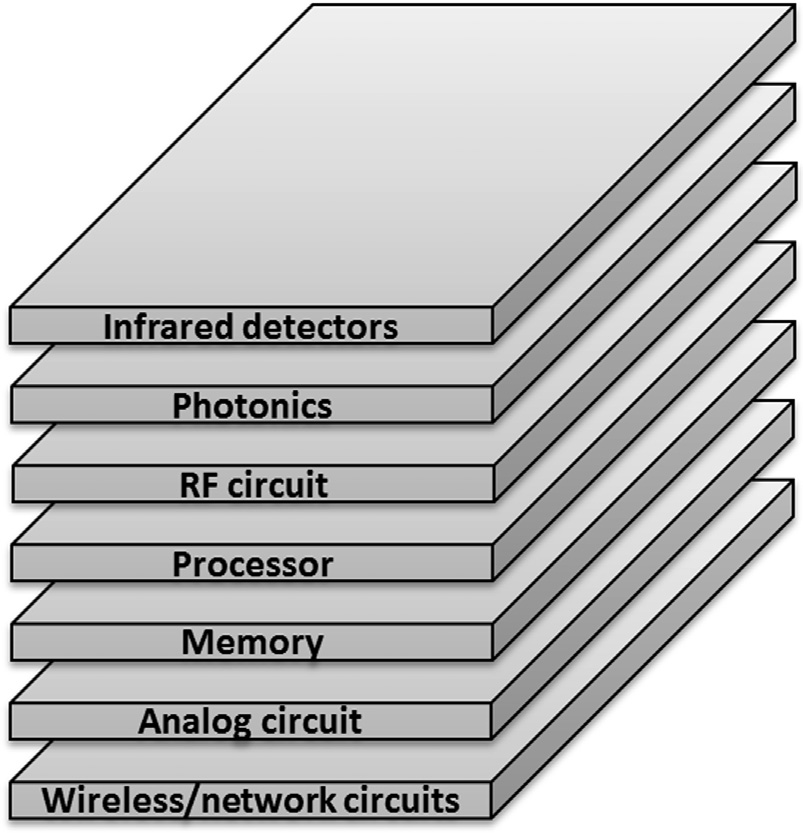
三维结构是集成异质电路的有效平台，如图5.1所示。三维集成电路的每一层通常使用不同的衬底材料独立开发，以适用于多种应用。一些现有研究已经探讨了硅衬底上同质电路（处理器/存储器堆栈）中硅通孔向衬底的噪声耦合问题[214,246]。在本节中，异质衬底材料被讨论，并提出了相应的噪声耦合模型。

5.1 异质衬底耦合

5.1.1 通用电路与兼容衬底类型

现代集成电路中一些常用的材料是硅（Si）、砷化镓（GaAs）、锗（Ge）和汞镉碲（HgCdTe）[247–249]。这些衬底材料各自最适合特定类型的电路功能。与前述其他材料相比，硅通常更为成熟且成本较低，因此广泛应用于主流处理器和存储器应用中。由于砷化镓具有优异的电子迁移率，使其在高性能模拟（以及部分数字）应用中具有吸引力，并且其直接带隙特性支持光系统应用。锗因其高吸收系数，是光伏和光电探测器应用的理想衬底材料。需要高质量红外探测器的特殊军事和空间应用通常使用汞镉碲（HgCdTe）[250]，其带隙可在0.1至1 eV范围内调节。该特性使汞镉碲可用于探测长波长光。

5.1.2 不同衬底材料的电阻特性

通用电路和兼容的衬底材料列于表5.1中。每种衬底材料的电电阻率也一并列出，该参数对噪声耦合过程有显著影响。由于表5.1中列出的电阻率范围较宽，因此在第5.2节中分别描述了每种衬底材料的个体噪声耦合特性。

表5.1 通用电路和兼容衬底类型
电路
------
处理器/存储器
射频/模拟
光子学
空间应用/探测器

5.1.3 不同衬底材料的噪声模型简化

针对上述每种衬底材料，分别描述了各自的衬底噪声模型。 [246]中提出的通用噪声耦合模型在 图5.2A 中提供以供参考。

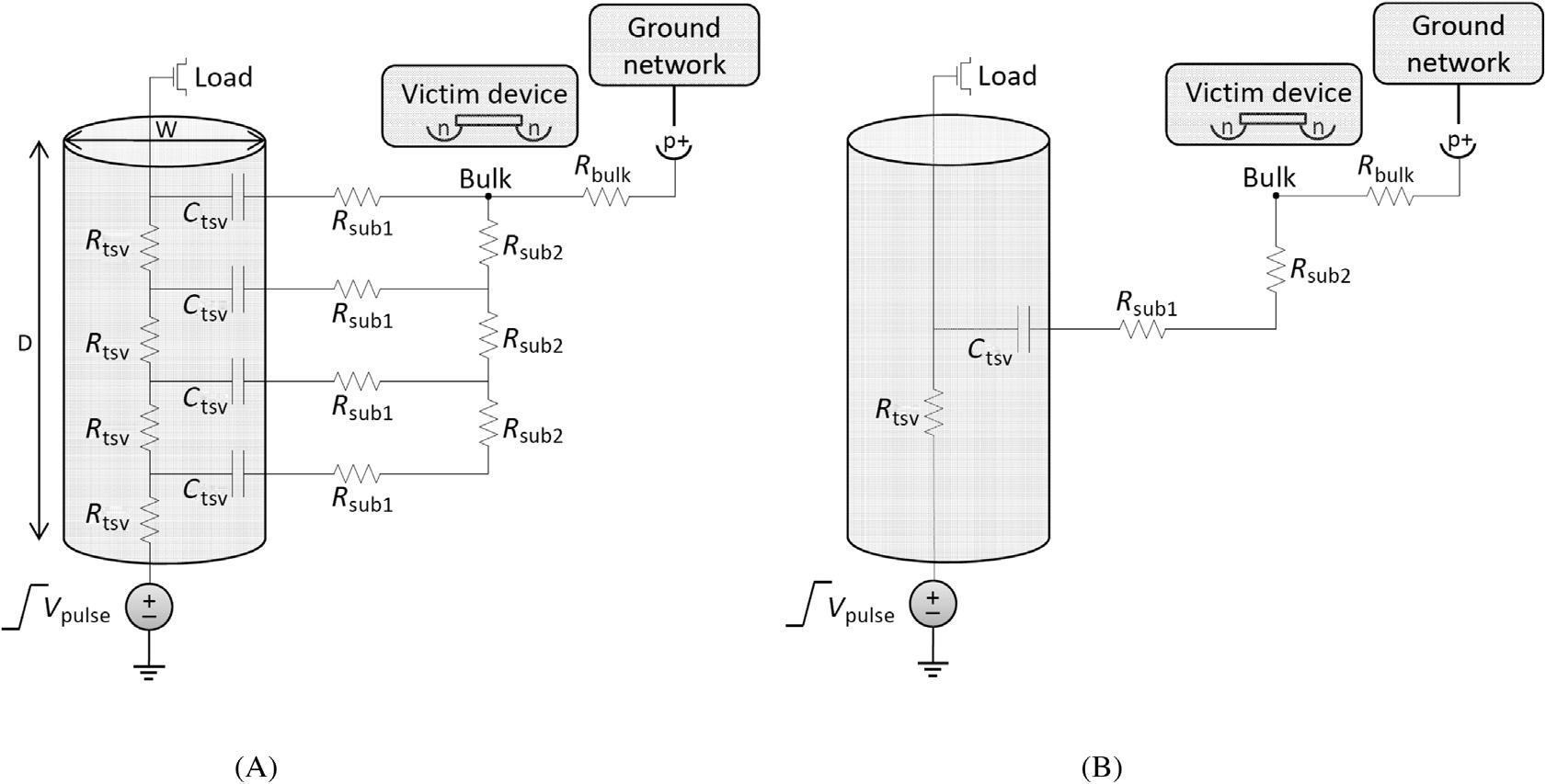通用模型，以及 (B) 简化模型)

一种由四个部分组成的分布RC模型用于表征硅衬底内硅通孔的阻抗和耦合电容。衬底采用分布横向和纵向电阻建模。地网络被建模为阻感（RL）阻抗[205]。图5.2A所示的模型表明对RC阻抗应采用分布模型。硅通孔的电阻为[246]

$$
R_{tsv} = \frac{1}{N_{tsv}} \cdot \frac{\rho_c D}{\pi(W/2)^2} \tag{5.1}
$$

一个TSV的分布段数量为$N_{tsv}$，TSV内导电材料的电阻率为$\rho_c$，TSV的深度（长度）和直径分别为$D$和$W$。当铜的电阻率为2.8 μΩ-cm[251]，深度为 20 μm，直径为 2 μm时[201]，TSV的电阻为0.18 Ω，对应$1/N_{tsv} = 1$。该电阻与典型数字缓冲器的输出电阻相比相对较小 [252]。因此，TSV采用集总RC模型表示，如图5.2B所示[244,253]。另一个重要问题是地网络的建模。受害器件通常通过体接触连接到地网络，因此该网络的电感行为也必须予以考虑。

集总模型与具有三个部分的分布模型在表5.2中针对硅、砷化镓和锗进行了比较。对于锗，还比较了第三种“短路”模型（如图5.3A所示）。该模型完全忽略了衬底电阻，因为衬底电阻可忽略不计，因此该模型仅表现出从硅通孔到衬底的耦合电容[252]。这些模型使用集成电路仿真程序（SPICE）进行评估。采用一个从0到1V的10 ps输入斜坡（Vpulse in图5.2）来模拟高活跃度数字电路的开关行为。在受害节点处评估电压，并记录三种不同地网络电感下的峰值噪声电压和建立时间（最终值的2%）。不同于本章中相邻互连之间的耦合[254]，在本章中描述了信号在干扰硅通孔中传播时对衬底的耦合。峰值噪声和建立时间是评估瞬态耦合噪声的充分指标。

表5.2 硅、砷化镓和锗的集总、分布和短路模型比较 衬底，针对地网络的不同电感值
模型
------
集总
分布 (三个部分)
短路

集总模型与分布模型相比在硅上的误差为1.2%。因此，集总模型可以准确表征硅衬底。从表5.2列出的结果可以看出，地网络的电感显著影响峰值噪声电压。在电感范围（从0.1到 10纳亨）内，峰值噪声电压的差异为26.5毫伏（14.2%）。汞镉碲的电阻率与硅相似。因此，在HgCdTe的噪声耦合分析过程中可以采用如图5.2B所示的相同模型。

砷化镓的集总模型和分布模型的峰值噪声电压均处于皮伏范围内，因此在大多数应用中可忽略不计。此种情况下的所提出的模型是一种“开路”模型，该模型忽略耦合电容，如图5.3B所示。注意表5.2 中地网络的电感对峰值噪声电压没有影响。这种行为是由于衬底的电阻率足够大，能够将地网络的电感旁路。

Ge对地网络的电感高度依赖。比较集总模型和分布模型，分布模型相较于集总模型在精度上几乎没有提升。峰值噪声电压的最大差异为0.2 mV（2.3%），而建立时间相似。因此，包含较少节点的集总模型更为可取。短路模型与集总模型相比，峰值噪声电压偏差为2.6 mV（23.4%），建立时间偏差为2 ns（25%）。集总模型类似于该模型的

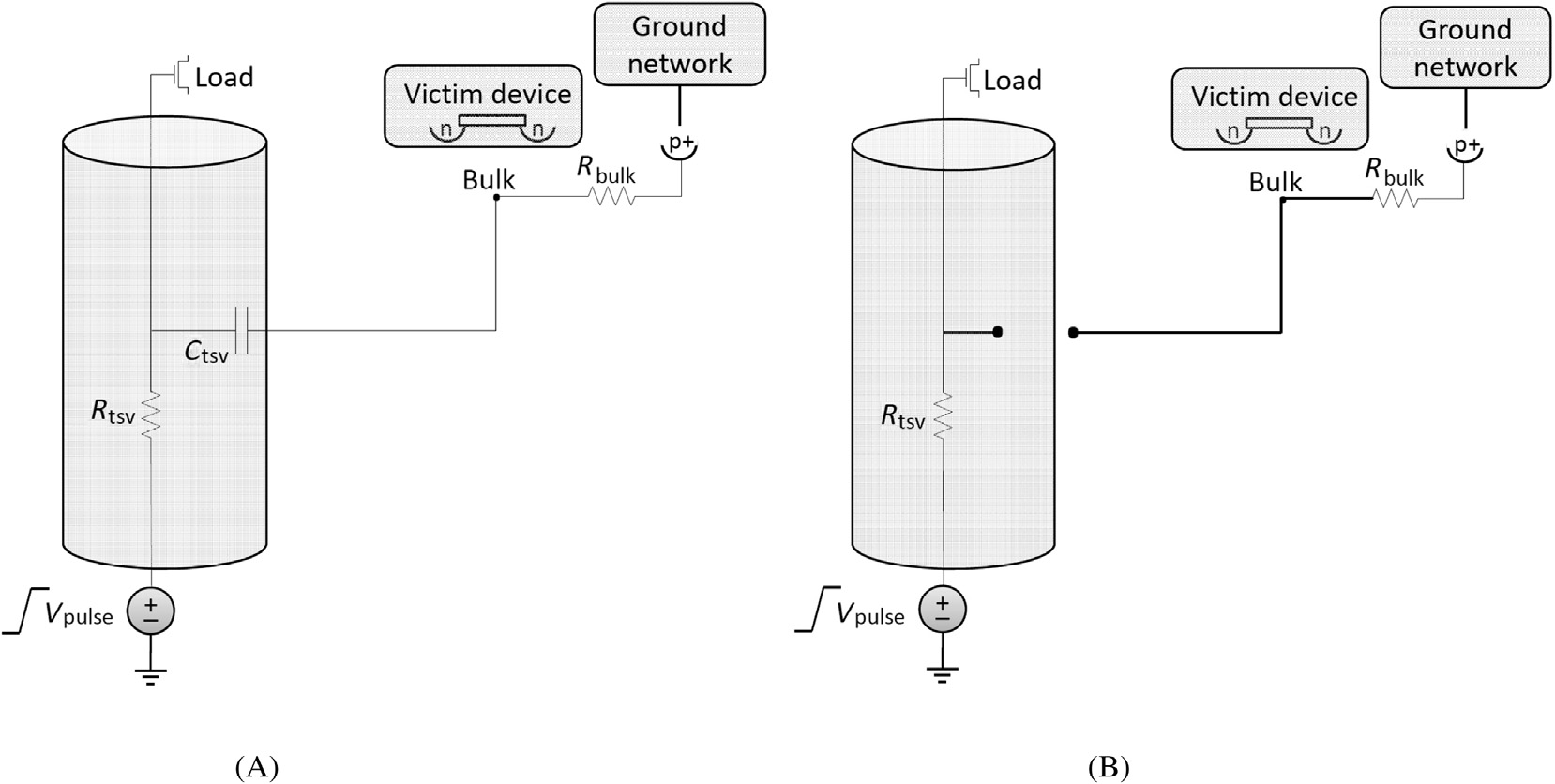
因此应使用硅（如图5.2B所示）。如果电路规格不是特别严格（允许较高的峰值噪声电压和较长的建立时间），则可以使用短路模型来减少计算量。

5.2 频率响应

本节提供了集总噪声耦合模型频率响应的特定技术分析。该分析仅限于最高达100GHz的频率范围。噪声隔离改进技术在第5.2.1节中提出。该模型在SPICE中进行评估，并根据第5.2.2节中讨论的每种衬底材料的特性提取系统的传输函数。在第5.3节，提取的传输函数在 MATLAB中进行评估，并与SPICE结果进行比较。由于碲镉汞和硅具有相似的电学特性，因此仅考虑硅、砷化镓和锗作为衬底材料。

5.2.1 噪声耦合系统的隔离效率

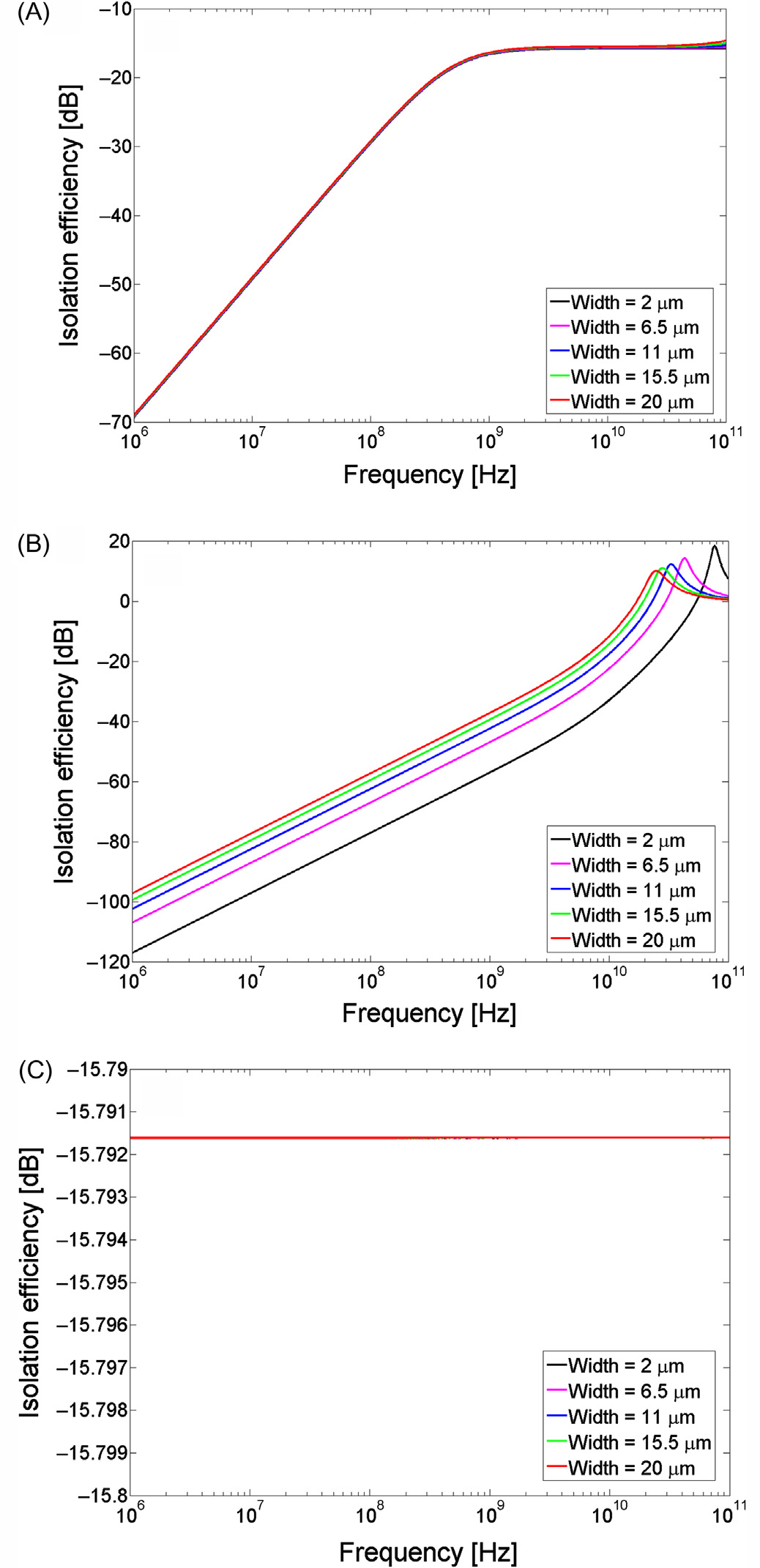
隔离效率是指在1V干扰信号下，在受害端观测到的信号幅度（单位为分贝）。不同衬底材料和地网络电感下的噪声耦合系统的隔离效率如图5.4所示，该结果来自SPICE仿真。锗的隔离效率对频率具有很强的依赖性，其次是硅，而由于砷化镓衬底的高电阻率，其几乎不随频率变化。尽管锗在很宽的频率范围（高达约10 GHz）内对频率有较强的依赖性，但其隔离效率仍高于砷化镓。锗系统中的频率相关元件降低了受害端的耦合噪声。如图5.4C所示，砷化镓的隔离效率与地网络电感无关。本节后续将讨论地网络电感对硅和锗的影响。

对于锗电路，谐振频率处于实际频率范围内。应采用特定技术来改善噪声隔离，以避免这些电路中产生高的耦合噪声。对于硅电路，隔离技术很大程度上取决于电路的工作频率和噪声指标。在数字CMOS电路中典型的信号跳变最大频率范围（低于10GHz）下，隔离效率较高。对于那些需要快速跳变且具有严格噪声指标的电路，应考虑使用隔离增强方法。对于砷化镓，隔离效率为−15.9分贝。应采用与频率无关的隔离技术，以进一步改善噪声隔离特性。

5.2.2 噪声耦合系统的传递函数

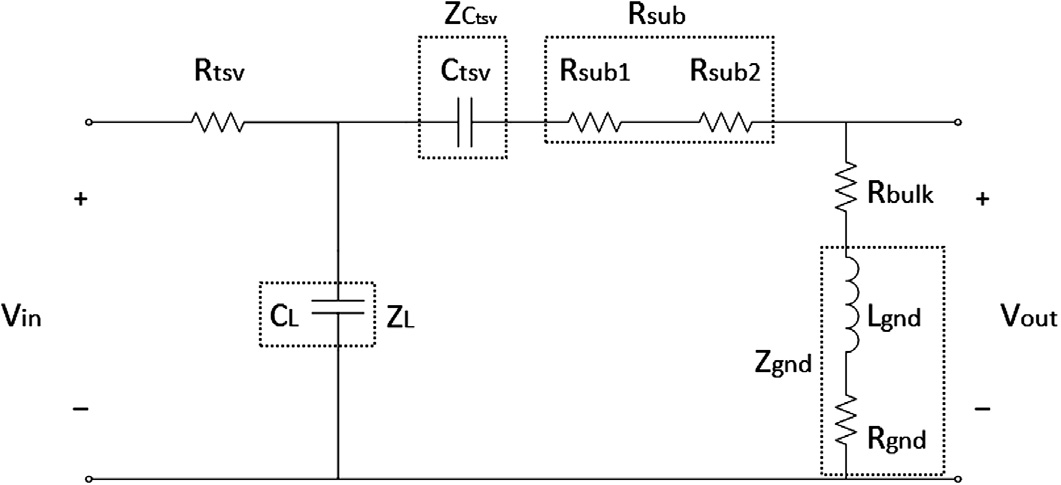
为了更好地评估噪声耦合机制，异构系统被表示为一个传递函数。该系统包括一个输入（干扰信号）和一个输出（受害模块处的信号）。系统的隔离效率[246,255]被描述，并提供各种技术。噪声耦合系统的信号等效电路如图5.5所示。图5.5中考虑了以下参数：

• 衬底阻抗：$R_{sub} = R_{sub1} + R_{sub2}$
• TSV耦合电抗：$X_{Ctsv} = \frac{1}{\omega C_{tsv}}$
• TSV耦合阻抗：$Z_{Ctsv} = j X_{Ctsv}$
• 接地网络电抗：$X_{gnd} = \omega L_{gnd}$
• 接地网络阻抗：$Z_{gnd} = R_{gnd} + j X_{gnd}$
• 负载电抗：$X_L = \frac{1}{\omega C_L}$
• 负载阻抗：$Z_L = -j X_L$

本章针对第5.1节讨论的基于衬底材料的异构系统描述了传递函数。第5.1节集总模型的传递函数是

$$
H(\omega) = \frac{V_{out}}{V_{in}} = \frac{(R_{bulk} + Z_{gnd}) Z_L}{(R_{tsv} + Z_L) (R_{sub} + R_{bulk} + Z_{Ctsv} + Z_{gnd}) + R_{tsv} Z_L} \tag{5.2}
$$

简化传递函数可得到一个更简单的模型，从而减少计算量。仿真负载电容（100 fF）相对较小，因此在假设为小信号模型（图5.5）并在实际频率范围（1 MHz 至 100 GHz）内工作时，该模型可视为开路。简化后的传递函数 $H(\omega)$ 是

$$
H(\omega) = \frac{R_{bulk} + Z_{gnd}}{R_{sub} + R_{bulk} + Z_{Ctsv} + Z_{gnd} + R_{tsv}} \tag{5.3}
$$

进一步降低(5.3)取决于特定层的衬底材料。在干扰源与受害端之间距离短至 10 μm时，硅和碲镉汞中的衬底和体电阻比TSV和接地网络电阻（$R_{sub}; R_{bulk} \gg R_{tsv}; R_{gnd}$）大三个到五个数量级。因此，表达式(5.3)简化为

$$
H(\omega) = \frac{R_{bulk} + j X_{gnd}}{R_{sub} + R_{bulk} + j(X_{gnd} - X_{Ctsv})} \tag{5.4}
$$

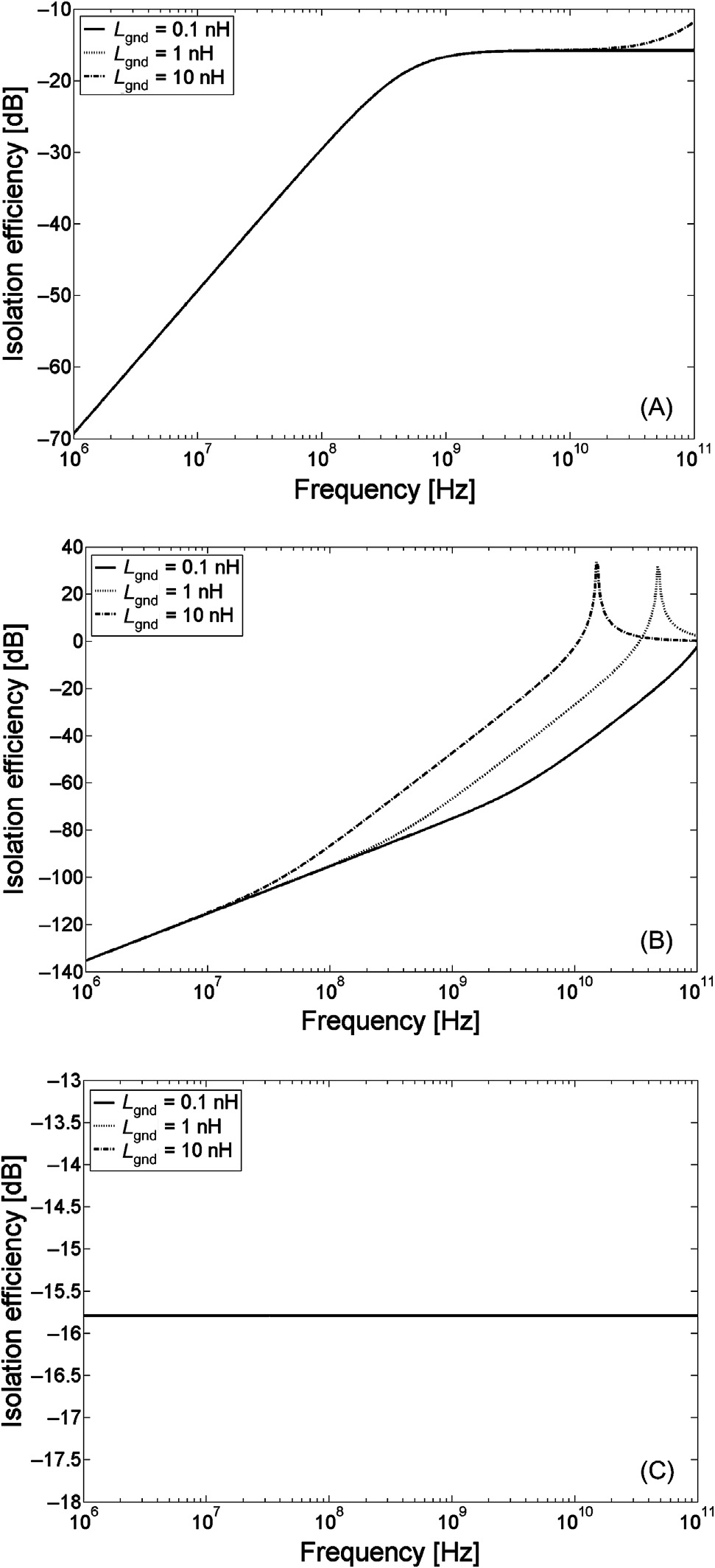
硅，(B) 锗，和 (C) 砷化镓)

对于锗，衬底和体阻抗与其他传递函数组件的相对大小相同，因此(5.2)无法进一步减小。锗的传递函数为

$$
H(\omega) = \frac{R_{bulk} + Z_{gnd}}{R_{sub} + R_{bulk} + Z_{Ctsv} + Z_{gnd} + R_{tsv}} \tag{5.5}
$$

砷化镓中的衬底和体电阻明显大于噪声耦合系统中所有其他组件（约六个数量级）。因此，传递函数简化为

$$
H(\omega) = \frac{R_{bulk}}{R_{sub} + R_{bulk}} \tag{5.6}
$$

代入衬底和体参数以及干扰硅通孔到受害端的最坏情况距离（10 μm）可得 $H(\omega) \approx 0.16$。以分贝为单位，砷化镓的隔离效率为 $20\log|H(\omega)| \approx -15.9\,\text{dB}$，如 图5.4C 所示。

5.3 提高噪声隔离的技术

在获得每种衬底类型的系统简化传递函数后，本节提出了一些用于减小耦合噪声的设计考虑。目标是通过调整不同的制造和设计参数来最小化$|H(\omega)|$，从而降低从干扰源耦合到受害端的噪声。本文提供了几种技术以改善异构三维电路中的噪声隔离。第5.3.1节讨论了地网络电感对噪声隔离的影响。第5.3.2节描述了干扰硅通孔与受害端之间的距离对噪声隔离特性的影响。

5.3.1 地网络电感

在集成电路电源分配网络的设计中，应考虑更薄且电阻更大与更厚且电感更大的金属互连之间的权衡（参见第18章，三维集成电路的供电）。在三维集成电路中，由于返回路径可能跨越整个三维结构，因此识别感性返回路径比在二维电路中更为复杂。因此，应特别强调低电感地线的设计。如图5.4所示，低电感地网络可直接改善硅和锗的耦合噪声系统的隔离效率。

对于锗而言，低电感地网络尤为重要。在电感性地网络情况下，隔离效率最差情况下的差异为73.5分贝。当地网络电感为10纳亨时，谐振频率为15.1吉赫兹；而当地网络电感为0.1纳亨时，谐振频率高于实际频率范围（>100 GHz）。谐振频率为 $f = 1/(2\pi\sqrt{LC})$，其中系统的电容为 $C$，地网络的电感为 $L$。如图5.4B所示，较低的地网络电感可使谐振频率移出实际频率范围。

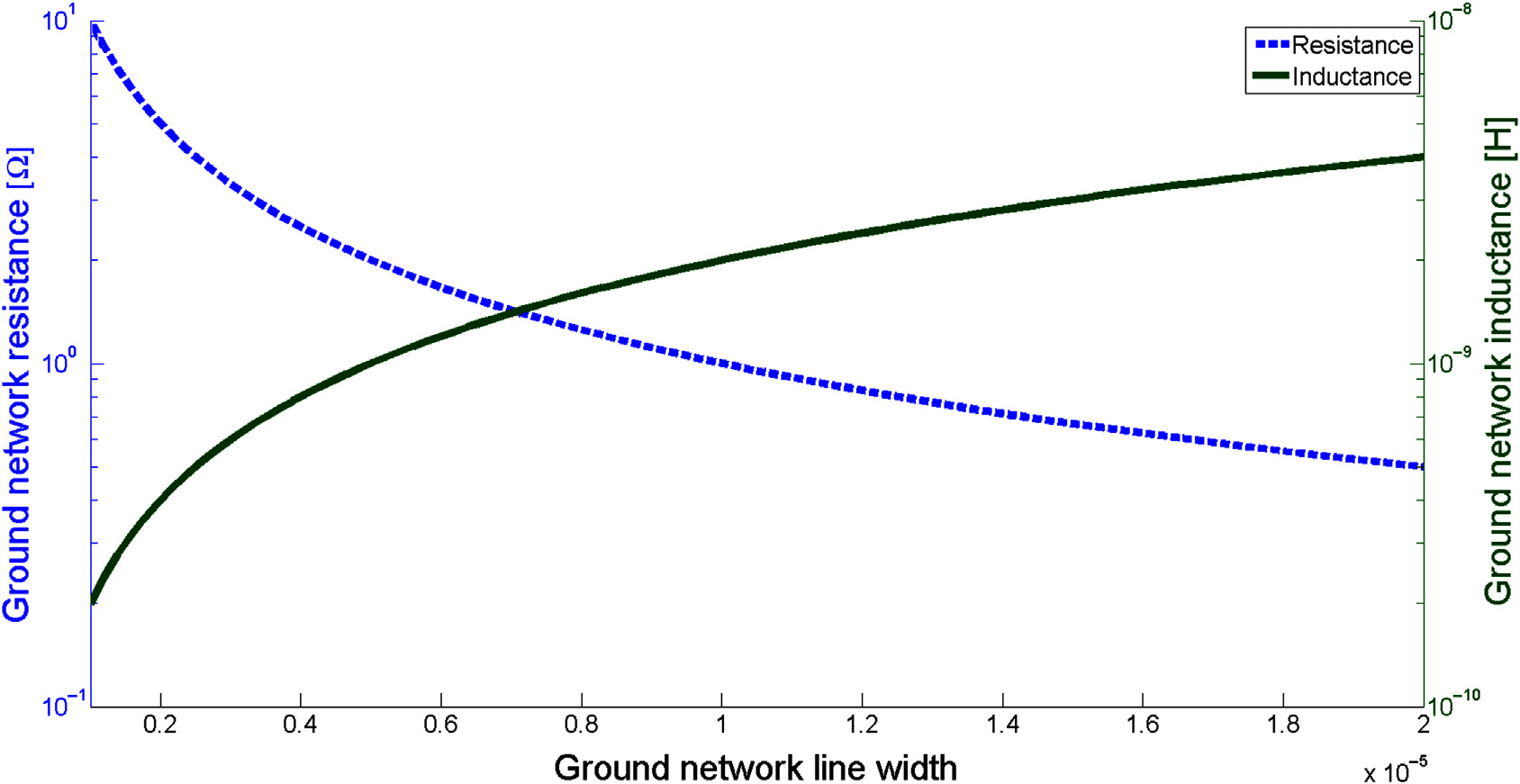
为了进一步验证该技术，针对每种衬底材料考虑了电感和电阻之间的权衡。地网络的电阻和电感随线宽的变化情况[185]如图5.6所示。

不同衬底材料的隔离效率通过以集成电路为重点的模拟程序（SPICE）进行仿真，结果如图5.7所示。对于硅衬底，实际频率范围在100 GHz以下，且线宽对地网络电感没有影响，因此应采用最小允许线宽。对于锗衬底，地网络的电阻与电感之间存在权衡关系。较宽的线路其峰值隔离效率低于较窄的线路。当线宽从2变化到 20 μm时，最差情况下的差异为8.2 dB。在56 GHz以下的频率范围内，窄线（2 μm）的隔离效率优于宽线（20 μm）。因此，锗衬底中地网络的线宽应根据信号转换频率来选择。对于砷化镓衬底，隔离效率与线宽无关，因此应使用允许的最小线宽。

硅，(B) 锗，和 (C) 砷化镓)

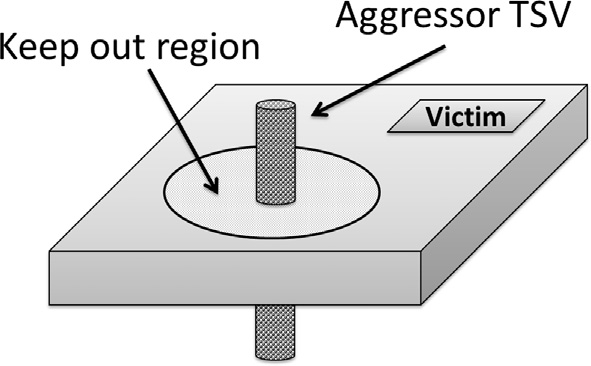
5.3.2 攻击者与受害者之间的距离

干扰模块“A”所在层m与受害模块“V”所在层n之间的距离如图5.8所示。单个硅通孔的深度（长度）以及从该硅通孔到受害端在层n上的水平距离分别为$D$和$l$。因此，模块“A”与“V”之间的距离为

$$
d_{AV} = \sqrt{(D \cdot |m-n|)^2 + l^2} \tag{5.7}
$$

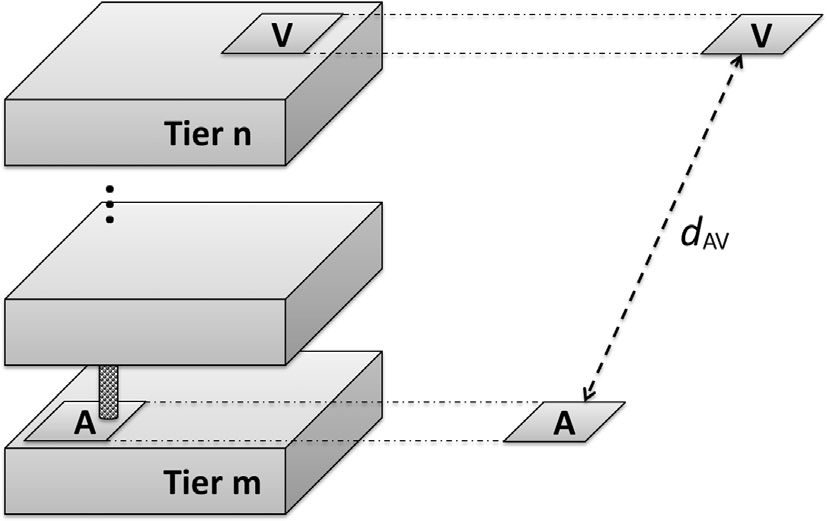
$d_{AV}$对锗的隔离效率的影响如图5.9所示。衬底厚度取决于硅通孔$D$的长度，范围从20到 60 μm，并且与异质衬底材料的不同制造工艺有关。同样，横向距离$l$的取值范围为10到 1000 μm。隔离效率提高了38.5分贝

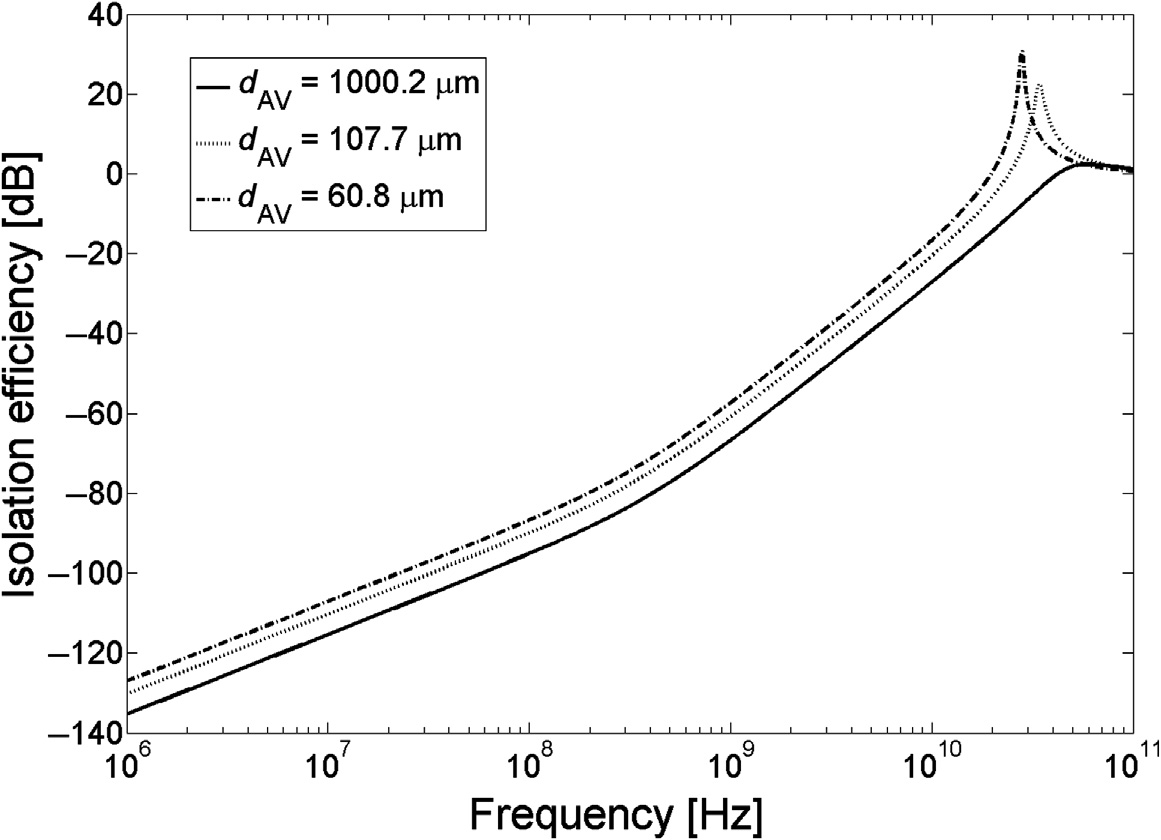
对于直径$d_{AV}$为1000.2 μm的情况，相较于直径$d_{AV}$为60.8 μm的情况进行了验证。将受害端电路远离承载干扰信号的硅通孔，可显著改善噪声隔离特性。或者，在干扰源与受害模块之间采用更厚的衬底或增加层的数量，仅能略微提高隔离效率，这是由于硅通孔的阻抗较低所致。

禁止区域（如图5.10所示）是围绕干扰硅通孔的一个圆形区域，受害端不应放置在该区域内，以确保耦合噪声低于$N_{\text{max}}$（最大允许噪声耦合，单位为分贝）。禁止区域的半径为$l$，满足 $20\log|H(\omega;l)| < N_{\text{max}}$。硅、锗和砷化镓的传递函数在(5.4)–(5.6)中的幅度分别为 (5.8)、(5.9)和(5.10)。

$$
|H(\omega; l)| = \left[
\left( \frac{R_{bulk}(R_{sub}(l)+R_{bulk}) + X_{gnd}(X_{gnd} - X_{Ctsv})}{(R_{sub}(l)+R_{bulk})^2 + (X_{gnd} - X_{Ctsv})^2} \right)^2 +
\left( \frac{X_{gnd}(R_{sub}(l)+R_{bulk}) - R_{bulk}(X_{gnd} - X_{Ctsv})}{(R_{sub}(l)+R_{bulk})^2 + (X_{gnd} - X_{Ctsv})^2} \right)^2
\right]^{1/2} \tag{5.8}
$$

$$
|H(\omega; l)| = \left[
\left( \frac{(R_{bulk}+R_{gnd})(R_{sub}(l)+R_{bulk}+R_{tsv}+R_{gnd}) + X_{gnd}(X_{gnd}-X_{Ctsv})}{(R_{sub}(l)+R_{bulk}+R_{tsv}+R_{gnd})^2 + (X_{gnd}-X_{Ctsv})^2} \right)^2 +
\left( \frac{X_{gnd}(R_{sub}(l)+R_{bulk}+R_{tsv}+R_{gnd}) - (R_{bulk}+R_{gnd})(X_{gnd}-X_{Ctsv})}{(R_{sub}(l)+R_{bulk}+R_{tsv}+R_{gnd})^2 + (X_{gnd}-X_{Ctsv})^2} \right)^2
\right]^{1/2} \tag{5.9}
$$

$$
|H(\omega; l)| = \frac{R_{bulk}}{R_{sub} + R_{bulk}} \tag{5.10}
$$

尽管 (5.8) 至 (5.10) 依赖于 $l$，但很难给出关于 $l$ 的闭式表达式。因此，针对每种衬底材料，根据相应的表达式生成设计空间，如 图5.11 所示。频率和 $l$均基于最大值耦合噪声（$N_{\text{max}}$）。由 (5.8)至 (5.10)生成的 Si、Ge 和 GaAs 的设计空间如 图5.11 所示。每个图表示噪声耦合系统的隔离效率随频率和 $l$ 的变化情况。

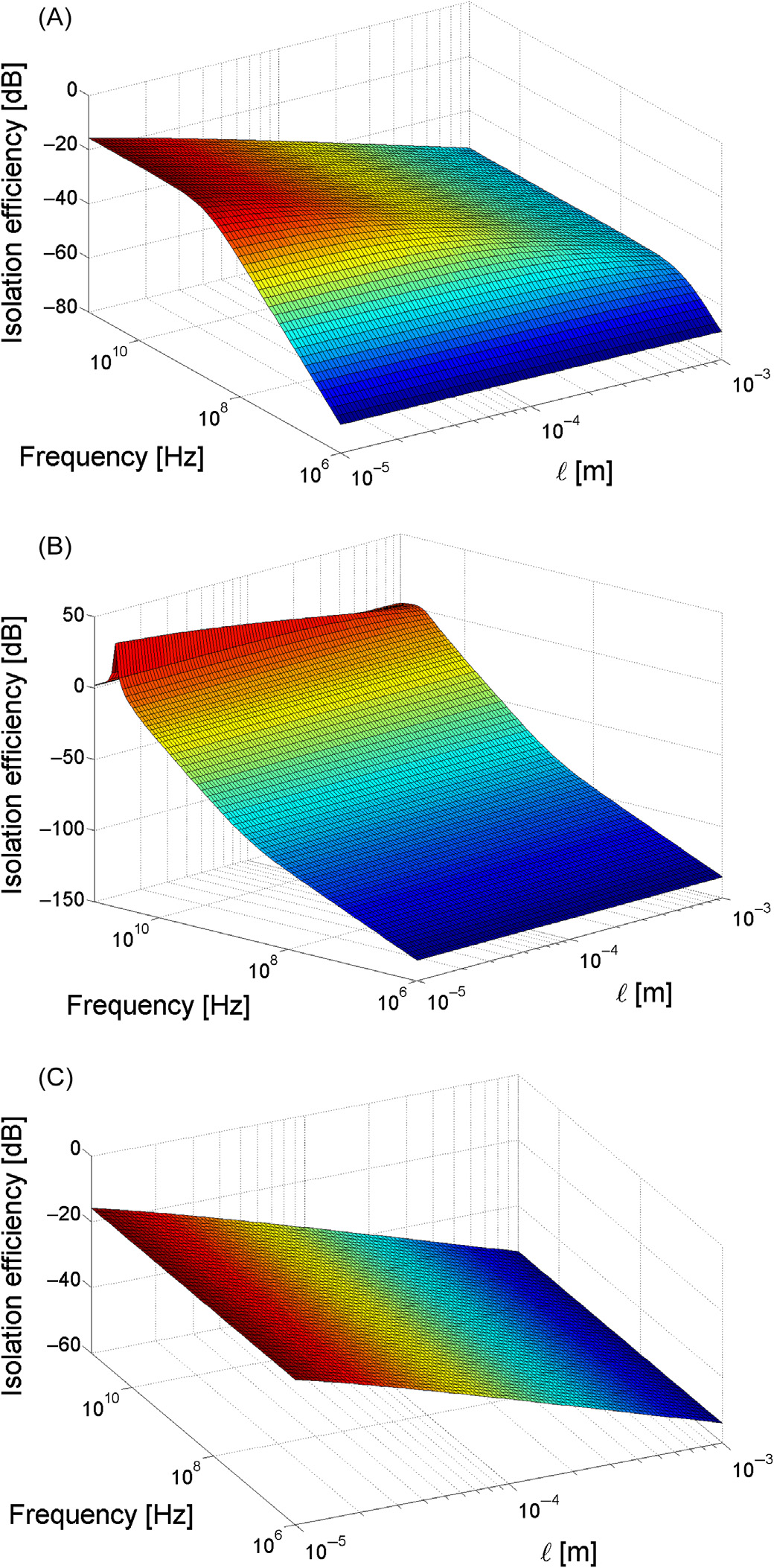硅，(B) 锗，和 (C) 砷化镓)

如 图5.11，受害端的噪声在低频时较小，并随着 $l$ 的增加而降低。增大 $l$可迅速降低 Si 和 GaAs 中的耦合噪声。而在 Ge 中，隔离效率对 $l$的依赖性较弱。这种行为是由于衬底电阻率可忽略不计，导致噪声耦合系统的频率依赖性更强。Ge 的谐振频率如 图5.11B 所示。因此应避免在谐振频率附近的设计空间。

为了量化设计空间内的禁止区域，可在 $N_{\text{max}}$ 上添加一个水平面，此处称为“基准面”。Si 衬底中禁止区域的一个示例如 图5.12 所示。在此情况下，$N_{\text{max}} = -40\,\text{dB}$，且禁止区域位于该水平面之上。该平面描述了在相关频率范围内，为保持隔离效率低于 $N_{\text{max}}$，干扰源与受害端之间的最小距离。可根据其他设计参数（例如 TSV 直径、TSV 填充材料、地网络阻抗和受害端尺寸）的传递函数生成类似的设计空间。

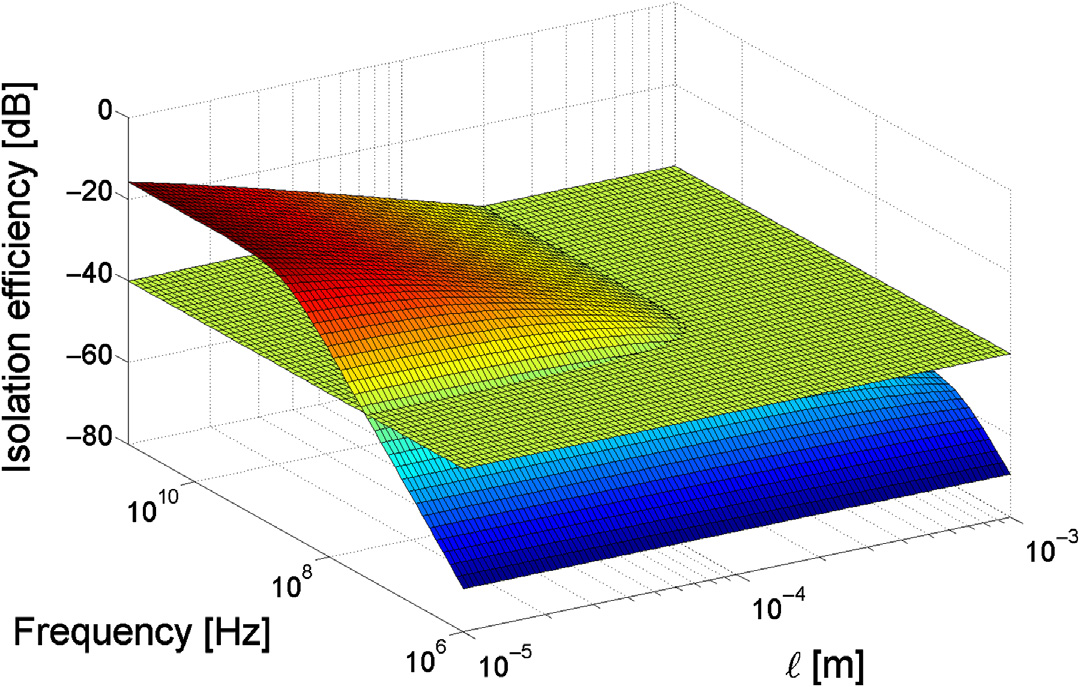
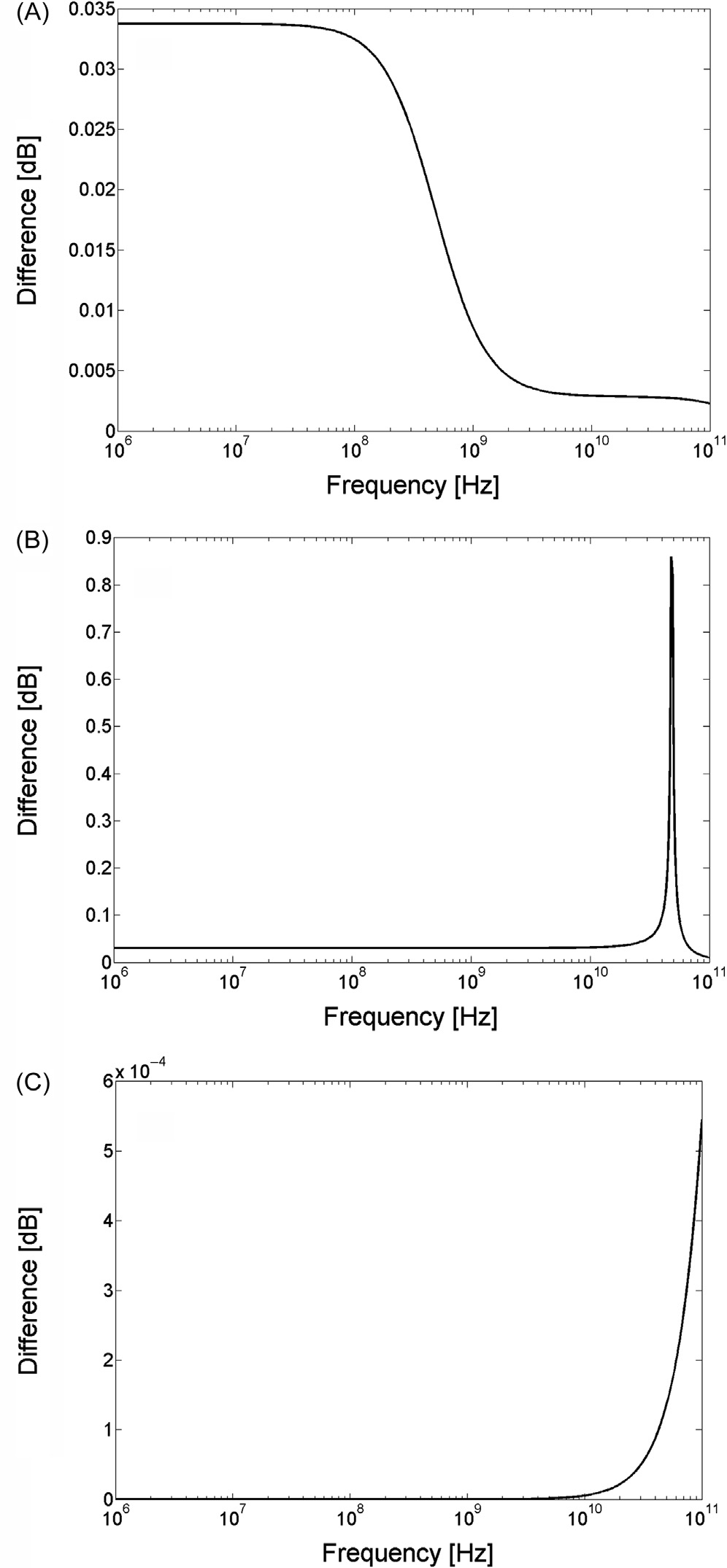
图5.13给出了硅、锗和砷化镓的传递函数与SPICE仿真之间的比较。该比较结果来源于 图5.11，在$l = 10\,\mu\text{m}$且地网络电感为1 nH的条件下获得。所有衬底材料的偏差均小于1分贝。

5.4 总结

异质3‐D系统内部存在着复杂的电子风暴。这种多导体系统会严重降低三维电路的性能。本章介绍了异质三维集成电路中的噪声耦合模型。这些模型考虑了异质3‐D系统内不同的衬底材料。

• 对于硅和锗衬底，集总模型已足够，与分布模型相比，其峰值噪声电压误差分别为26.5 mV和0.2 mV。
• 对于锗衬底，可采用短路模型以满足较宽松的噪声约束。
• 碲镉汞的电学特性与硅相似，因此适用于硅的模型也适合此类衬底。
• 砷化镓衬底为高阻特性，能有效隔离受害端与干扰源，因此对砷化镓衬底采用开路模型。
• 噪声耦合系统可用传递函数表示，以评估其隔离效率特性。降低传递函数的幅值，从而减小耦合噪声，是设计目标。
• 传递函数可根据衬底特定参数进行简化。每个简化传递函数可用于生成不同材料和设计参数下的设计空间。
• 简化传递函数与SPICE仿真结果对比，在实际频率范围（高达100 GHz）内表现出良好的一致性。
• 调节地网络电感这一隔离改进技术，可将谐振频率移出感兴趣的频率范围，从而降低耦合噪声。
• 禁止区域作为一种隔离改进技术，通过增加干扰硅通孔与受害端之间的水平距离来实现。针对每种衬底材料，设计空间由禁止区域和频率共同描述。