空间谱估计就是利用空间阵列实现空间信号的参数估计的一项专门技术。下图为空间谱估计的系统结构。目标空间代表我们所要感知的环境,在这个环境中包含着多个来自不同方向的目标入射信号。观察空间则可以表示成我们的雷达天线,由按照一定方式排列的阵元组中,图中通道代表着我们的接收天线。估计空间则表示我们的信号处理模块,从观察空间得到的信号数据在估计空间,即处理器中进行处理,并还原出真实的目标信号源数和入射角。

将观察空间再细化,得到下面的阵列测向基本模型,其中,M为阵列接收天线个数,θ为信号入射角。

接下来,我们考虑多个信号源入射到空间阵列的数学模型,这部分为空间谱估计理论的基础,也是后续DML , DBF,MUSIC,Capon等DOA估计方法的理论基础。
1.1通常情况下的数学模型
假设有N个原场窄带(Bw<<Freq)信号入射到具有M个阵元的某阵列上,通过观察空间采集到的数据,在估计空间上信号可用如下的复包络形式表示:

(4.1.1a)
式中,
![]()
是接收信号的幅度,
![]()
是接收信号的相位,
![]()
是接收信号的频率,在窄带远场信号源的假设下,有

(4.1.1b)
根据式(4.1.1a)和式(4.1.1b),可以得到下式:
![]()
(4.1.2)
因此,第l个阵元的接收信号表示为

(4.1.3)
上式中,
![]()
为第l个阵元对第i个信号的增益,
![]()
表示第l个阵元在t时刻的噪声,
![]()
表示第i个信号到达第l个阵元时相对于参考阵元的时延。
将M个阵元在特定时刻接收到的信号排列成一个列矢量,可得

(4.1.4)
假设每个接收阵元间互不干扰,则
![]()
可以归一化为1,因此上式可以简化为

(4.1.5)
将式(4.1.5)写成矢量形式如下:
![]()
(4.1.6)
式中,X(t)为阵列的M x 1维快拍数据矢量,N(t)为阵列的M x 1维噪声数据矢量,S(t)为空间信号的N x 1维矢量,A为空间阵列的M x N维阵列流型矩阵(导向矢量阵),且

(4.1.7a)
其中,导向矢量

(4.1.7b)
式中,
![]()
, c为光速,
![]()
为波长。
根据上述公式,要获得导向矢量则需要知道τ(相位时延)的值,根据空间几何关系,可以知道阵元间的相位时延表示如下

(4.1.8)
几何模型如下图,

因此,关键在于求得不同阵列中各阵元间相位时延的值。
根据我们平常所用到的阵列类型,这里介绍两种阵列的阵元间相位延迟计算方式。
(1)平面阵
设阵元的位置为
![]()
,以原点为参考点,另假设信号入射参数为
![]()
,分别表示方位角与俯仰角,其中方位角表示与x轴的夹角,则有
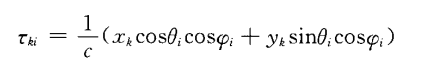
(4.1.9a)
(2)线阵
设阵元的位置为
![]()
,以原点为参考点,另假设信号入射参数为
![]()
,表示方位角,其中方位角表示与y轴的夹角(即与线阵法线的夹角),则有

(4.1.9b)
1.2DBF(数字波束形成)
对于接收信号形如下式

(4.3.1)
我们可以构造出一个导向矢量来,其中的角度任意给定(盲猜,不妨设为α),那么就可以构造出一个来波方向为α的导向矢量为

(4.3.2)
用我们盲猜的这个导向矢量a (α)和接收信号做向量内积,即

(4.3.3)
得,

(4.3.4)
从上式我们可以看到,等号在α = θ时取得。
通过这个不等式可知,如果我们盲猜对了,即α = θ,那么得到的结果是一个最大值。
因此,我们可以把所有的角度都猜一遍,找出那么结果结果最大的,其对应的角度就是我们DOA估计的结果。
常规DBF计算步骤如下:

同时,这里贴出我们常用的FFT求解角度原理,以供参考

根据上述推论,MATLAB仿真代码部分截图如下

仿真结果如下,可以看到DBF也能区分多个目标,单快拍即可解出,但无法突破瑞利限。

更多内容,可关注微信公众号:RADAR驿站


























 7672
7672

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








