【2020模拟赛day7】D. 回文子串_d - 回文子串-优快云博客

本文链接：https://blog.youkuaiyun.com/andyc_03/article/details/110004210

本文探讨了一种优化算法，通过预处理posl和posr数组，降低了计算F[i][j]——i-j本质不同子序列个数时的复杂度。举例说明了如何利用区间移动策略，仅维护每个字符的影响，从而实现85分的期望效率。代码展示了如何在C++中实现这一高效解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

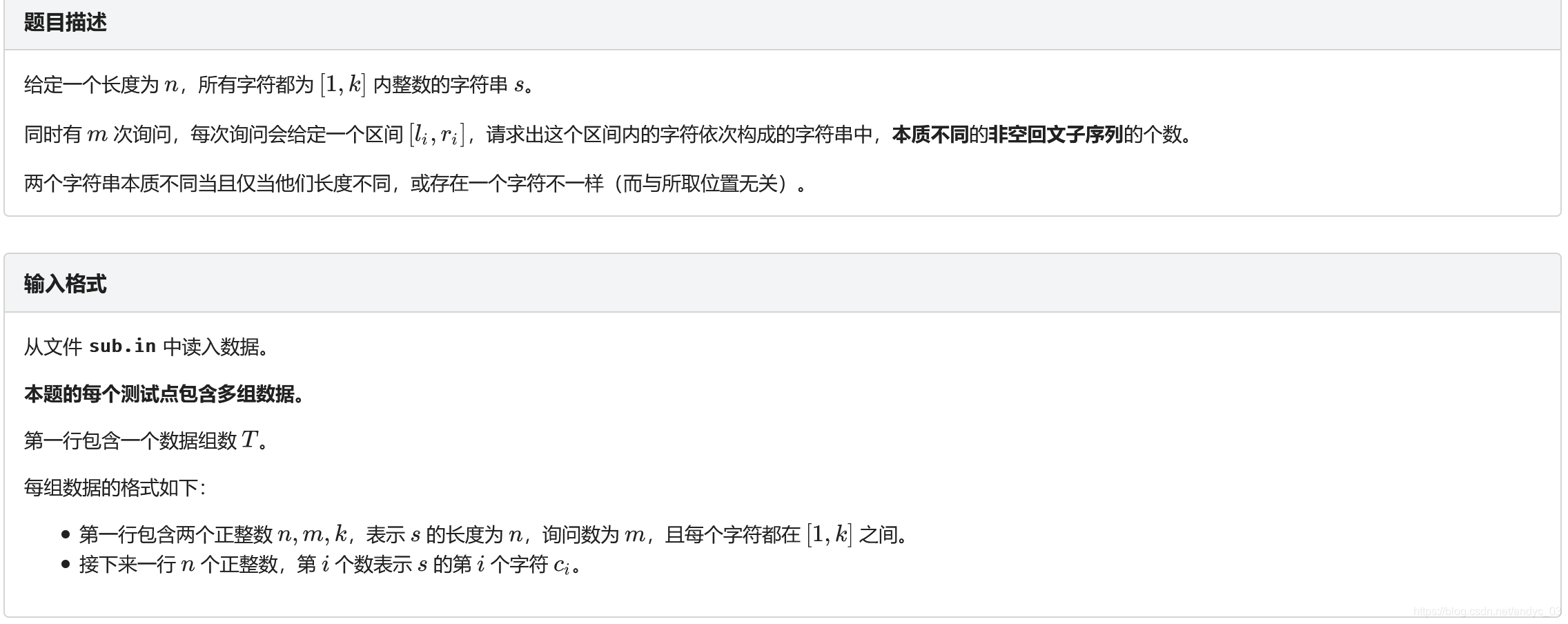
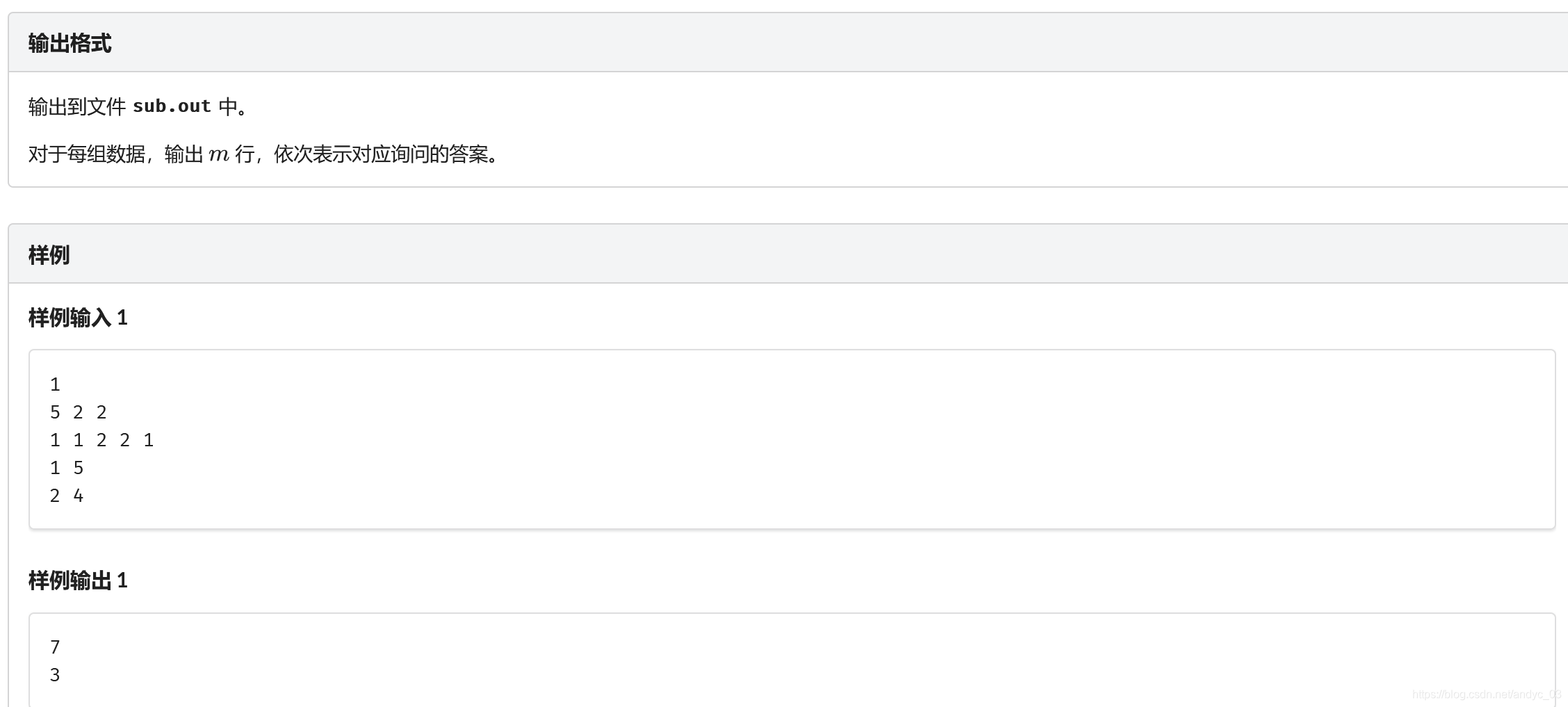
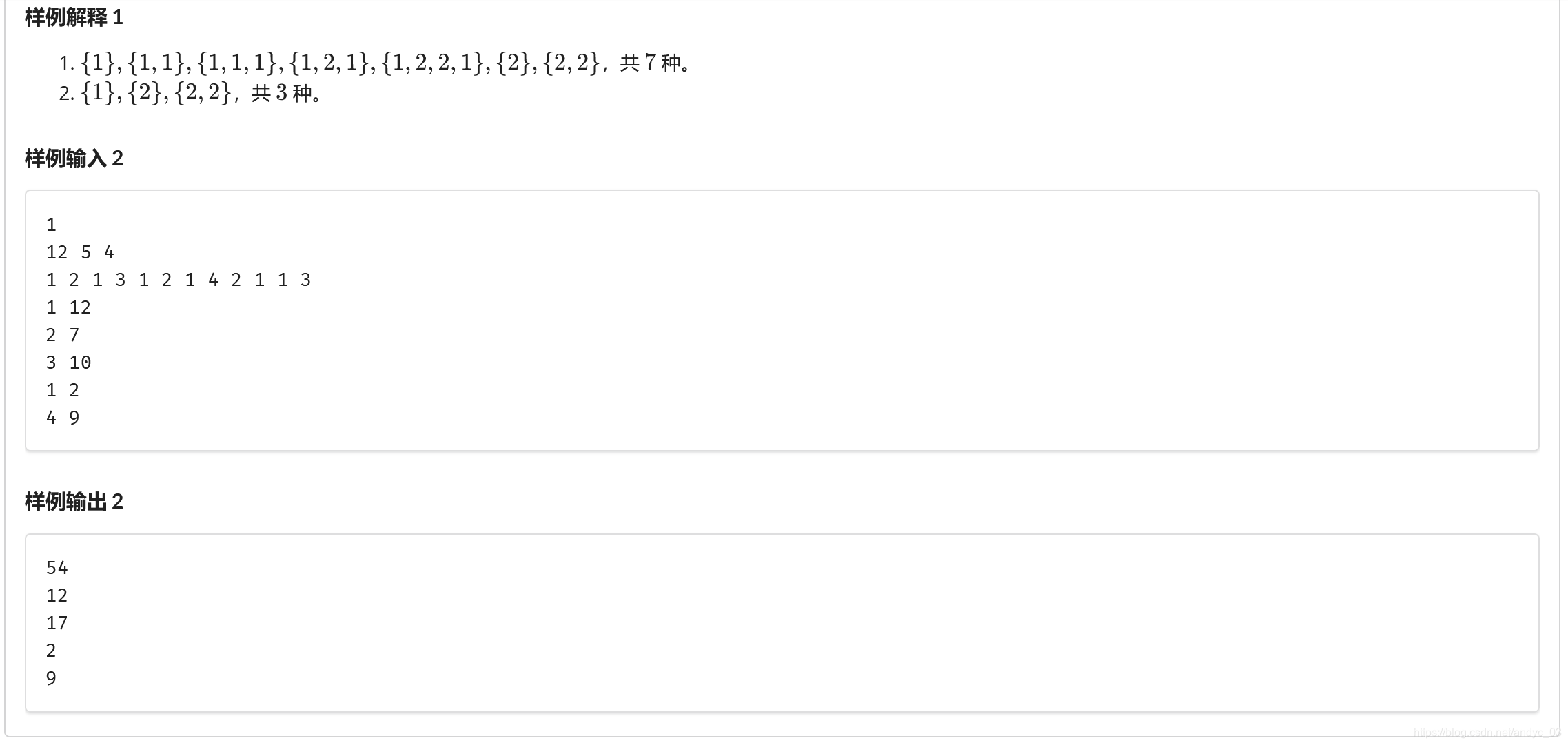
F[i][j]表示 i-j 的本质不同的会问子序列的个数

举个例子：

1 1 2 2 1

预处理一下posl[c][l][r]和posr[c][l][r]

表示字符c在区间l-r的最靠左/右的位置

for(int len=1;len<=n;len++)

for(int l=1;l+len-1<=n;l++)

{

int r=l+len-1;

for(int k是字符)

f[i][j]+=f[posl[k][l][r]+1][posr[k][l][r]-1]+1;

}

这个方法的期望的得分 85pts

优化：考虑区间每次只移动一个位置，只会对最多两个字符造成影响，我们可以去维护一下每个字符的和

这题的取模是不是忘写在题面了？？看了标程才知道啊

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=6005;
const int mod=1e9+7;
ll f[maxn][maxn];
int n,m,k,a[maxn],l[maxn],r[maxn],tmp[maxn];
int main()
{
	freopen("sub.in","r",stdin);
	freopen("sub.out","w",stdout);
	int t,x,y; scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d%d",&n,&m,&k);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		for(int i=n;i>=1;i--)
		{
			for(int j=1;j<=k;j++)
				l[j]=0,r[j]=0,tmp[j]=0;
			int cnt=0,res=0;
			for(int j=i;j<=n;j++)
			{
				if(!l[a[j]]) l[a[j]]=j,cnt++;
				r[a[j]]=j;
				if(l[a[j]]!=r[a[j]])
				{
					res-=tmp[a[j]];
					if(res<0) res+=mod;
					res+=f[l[a[j]]+1][r[a[j]]-1]+1;
					res%=mod;
					tmp[a[j]]=f[l[a[j]]+1][r[a[j]]-1]+1; 
				}
				f[i][j]=res+cnt;
				f[i][j]%=mod;
			}
		}
		for(int i=1;i<=m;i++)
		{
			scanf("%d%d",&x,&y);
			printf("%lld\n",f[x][y]);
		}
	}
	return 0;	
}