【2020模拟赛day5】D. 砍树问题

最新推荐文章于 2025-05-24 09:58:06 发布

andyc_03

最新推荐文章于 2025-05-24 09:58:06 发布

阅读量281

点赞数

CC 4.0 BY-SA版权

分类专栏：算法动态规划文章标签：算法

本文链接：https://blog.youkuaiyun.com/andyc_03/article/details/109700637

算法同时被 2 个专栏收录

218 篇文章

订阅专栏

动态规划

35 篇文章

订阅专栏

这篇博客介绍了如何使用树形动态规划（DP）解决关于连通块的问题，并展示了如何在代码中实现。在初始的代码基础上，为了处理大整数，博主引入了高精度计算，这一部分的实现经历了一些挑战。最终，通过高精度乘法的改进，成功解决了题目需求。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

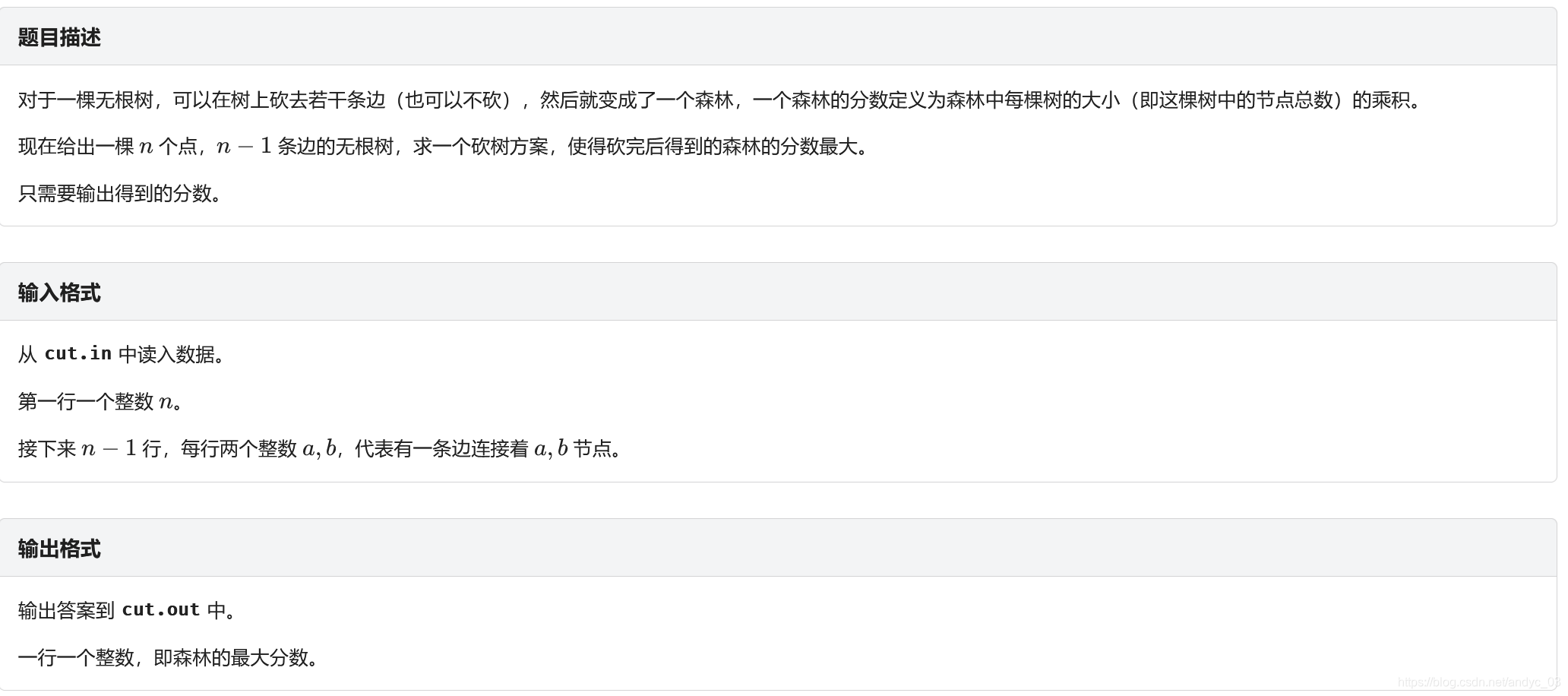
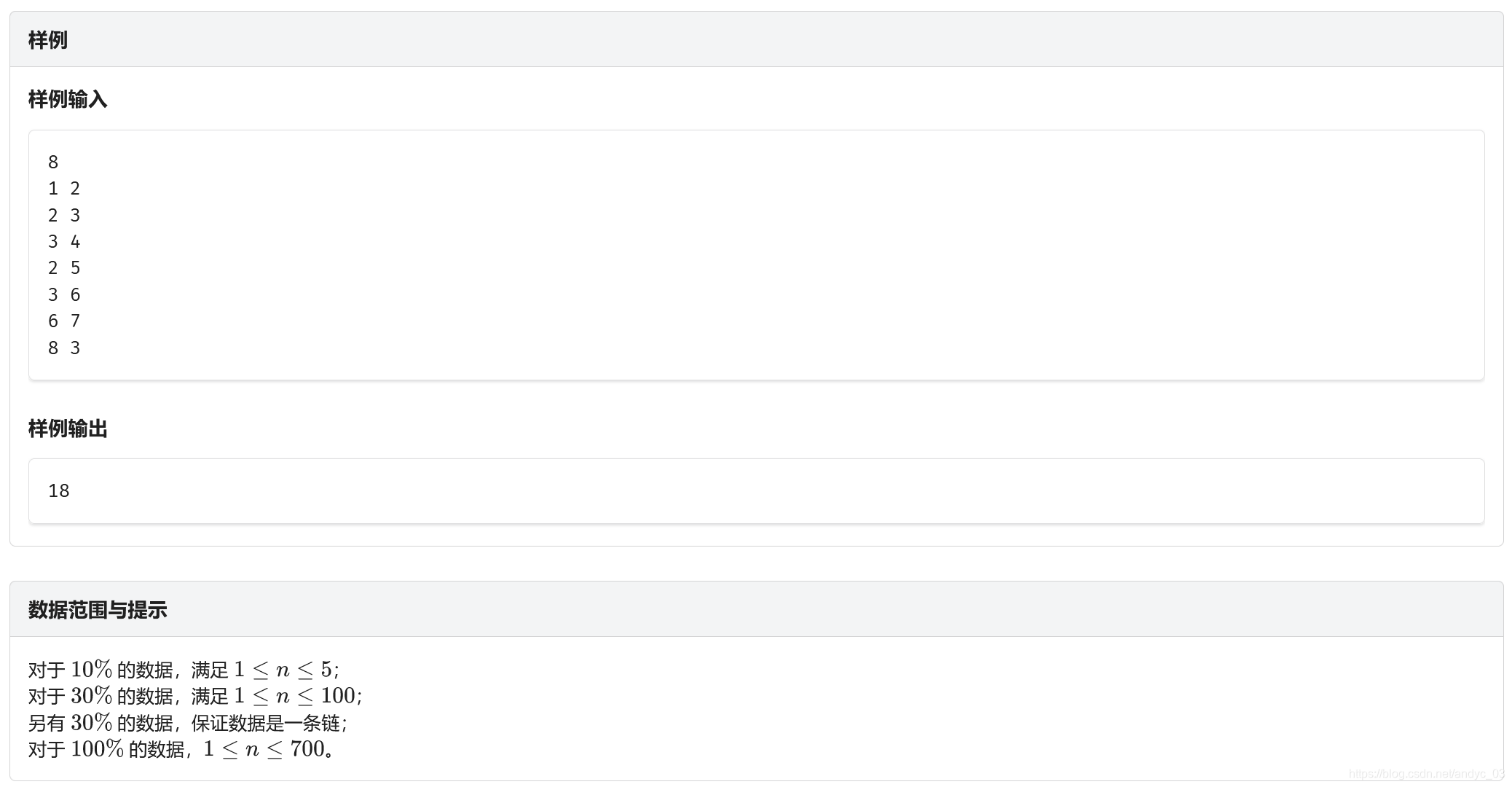
很显然是一个树形dp

f[i][j]表示以 i 为根的子树中所属的连通块大小为 j 时的最大值

那么可以用f[i][j]*f[son[i]][k]去更新f[i][j+k]

得到代码

#include<bits/stdc++.h>
using namespace std;
int n;
const int maxn=705;
int head[maxn],cnt;
struct edge
{
	int to,nxt;
}e[maxn<<1];
void add(int x,int y)
{
	e[++cnt].to=y;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}
int dep[maxn],size[maxn];
long long f[maxn][maxn];
void dfs(int u,int fa)
{
	size[u]=1;
	for(int i=0;i<=n;i++) f[u][i]=1;
	for(int i=head[u];i;i=e[i].nxt)
	{
		int to=e[i].to;
		if(to==fa) continue;
		dfs(to,u);
		for(int j=size[u];j>=0;j--)
			for(int k=size[to];k>=0;k--)
				f[u][j+k]=max(f[u][j+k],f[u][j]*f[to][k]);
		size[u]+=size[to];
	}
	for(int i=1;i<=size[u];i++)
		f[u][0]=max(f[u][0],f[u][i]*i);
}
int main()
{
	freopen("cut.in","r",stdin);
	freopen("cut.out","w",stdout);
	scanf("%d",&n);
	int x,y;
	for(int i=1;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}	
	dfs(1,0);
	printf("%lld\n",f[1][0]);
	return 0;
}

但是这道题还需要高精度！！

代码

#include<bits/stdc++.h>
using namespace std;
int n;
const int maxn=705;
int head[maxn],cnt,bit=10000;
struct edge
{
	int to,nxt;
}e[maxn<<3];
void add(int x,int y)
{
	e[++cnt].to=y;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}
int size[maxn];
struct bignum
{
	int a[105];
	int len;
}f[maxn][maxn];
bignum change(int x)
{
	bignum tmp;
	tmp.len=1; tmp.a[1]=x;
	return tmp;
}
bignum operator *(bignum x,bignum y)
{
	bignum res;
	memset(res.a,0,sizeof(res.a));
	for(int i=1;i<=x.len;i++)
		for(int j=1;j<=y.len;j++)
			res.a[i+j-1]+=x.a[i]*y.a[j];
	int len=x.len+y.len-1;
	for(int i=1;i<=len;i++)
		res.a[i+1]+=res.a[i]/bit,res.a[i]%=bit;
	if(res.a[len+1]) len++; 
	res.len=len;
	return res;
}
bignum mmax(bignum x,bignum y)
{
	if(x.len>y.len)
		return x;
	if(x.len<y.len)
		return y;
	for(int i=x.len;i;i--)
	{
		if(x.a[i]>y.a[i])
			return x;
		if(y.a[i]>x.a[i])
			return y;
	}
	return x;
}
void dfs(int u,int fa)
{
	size[u]=1;
	f[u][1].len=f[u][1].a[1]=1; 
	for(int i=head[u];i;i=e[i].nxt)
	{
		int to=e[i].to;
		if(to==fa) continue;
		dfs(to,u);
		for(int j=size[u];j>=0;j--)
			for(int k=size[to];k>=0;k--)
				f[u][j+k]=mmax(f[u][j+k],f[u][j]*f[to][k]);
		size[u]+=size[to];
	}
	f[u][0]=change(size[u]);
	for(int i=1;i<=size[u];i++)
		f[u][0]=mmax(f[u][0],f[u][i]*change(i));
}
int main()
{
	freopen("cut.in","r",stdin);
	freopen("cut.out","w",stdout);
	scanf("%d",&n);
	int x,y;
	for(int i=1;i<n;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}	
	dfs(1,0);
	printf("%d",f[1][0].a[f[1][0].len]);
	for(int i=f[1][0].len-1;i;i--)
		printf("%.4d",f[1][0].a[i]);
	return 0;
}

高精度乘法写炸了好几次！！！