牛客OI周赛15-提高组环球旅行

最新推荐文章于 2021-07-23 16:10:41 发布

原创最新推荐文章于 2021-07-23 16:10:41 发布 · 175 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法专栏收录该内容

218 篇文章

订阅专栏

本文介绍了一种利用树形动态规划方法求解树上直径问题的算法，通过预处理从直径两端出发的子树直径，实现快速枚举删除直径上的任意边，以寻找使树上最大距离最小的方案。

题目链接

题目描述：

给定一棵大小为n的树，让你断一条边，使得树上距离最大值最小。

考虑到最后要求树上最大距离最小，我们能想到一定断开树上直径的一条边（否则，直径将保留，就不是最优了）
然后，我们可以枚举断开每一条边，然后去统计两棵子树的直径
但是这样做显然是会超时的

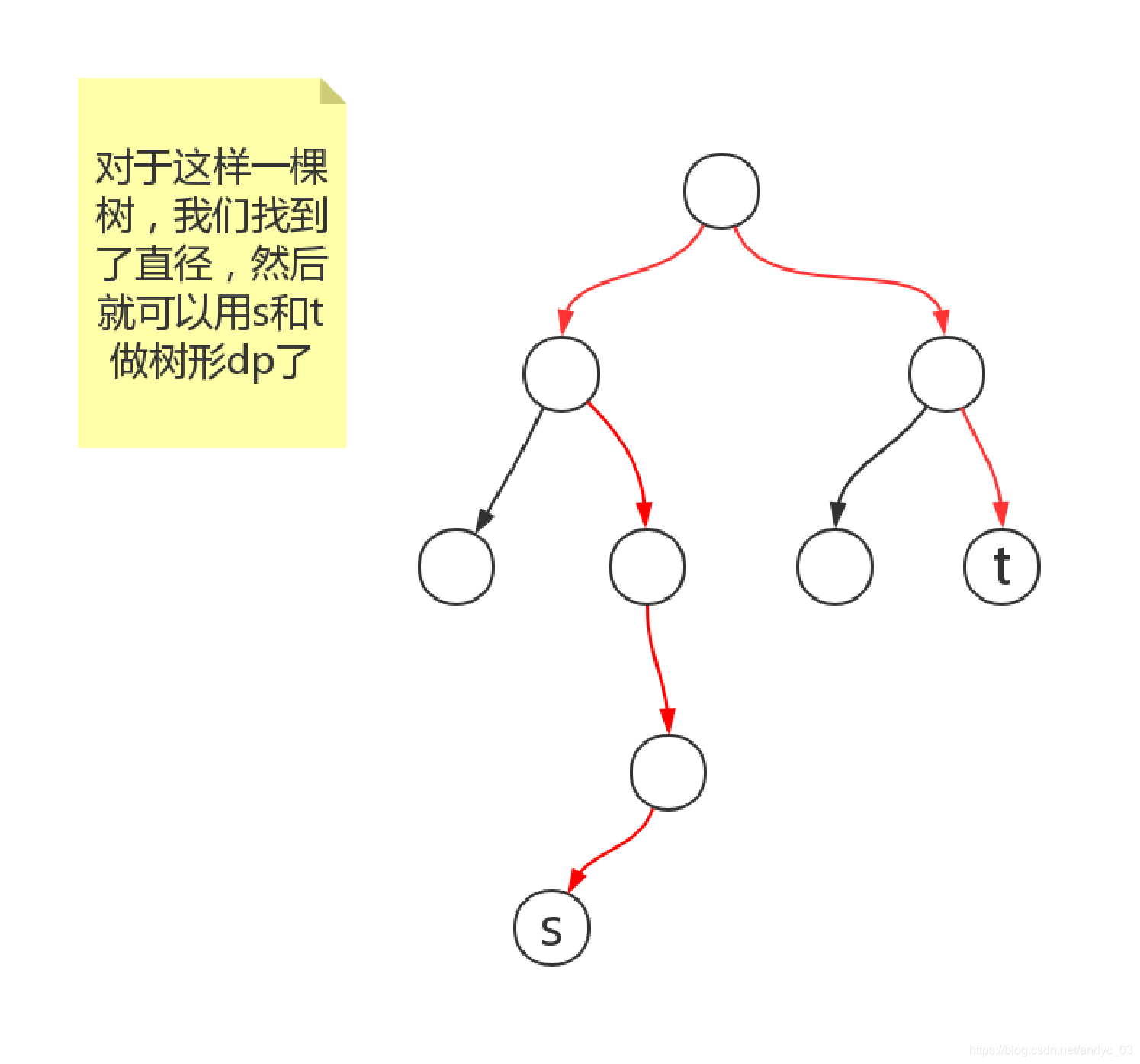
那么我们可以使用树形dp的方法，处理出从直径的两个端点s和t，出发，每个子树的树的直径，这样就能快速的枚举删掉直径上大哪条边了

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
int n,s,t,head[maxn],cnt,len,fa[maxn],dp[maxn],son[maxn],dp1[maxn],dep[maxn];
struct edge
{
	int to,nxt,v;
}G[maxn<<1];
void add(int x,int y,int z)
{
	G[++cnt].to=y;  G[cnt].nxt=head[x]; G[cnt].v=z; head[x]=cnt;
}
void dfs(int x,int f,int d)
{
	if(len<d){len=d; s=x;}
	for(int i=head[x];i;i=G[i].nxt)
	{
		int to=G[i].to;
		if(f==to) continue;
		dfs(to,x,d+G[i].v);
	}
	return;
}
void dfs1(int x ,int f)
{
	fa[x]=f;
	int p=0;
	for(int i=head[x];i;i=G[i].nxt)
	{
		int to=G[i].to,v=G[i].v;
		if(f==to) continue;
		dfs1(to,x);
		dp[x]=max(dp[x],dp[to]);
		if(p<dep[to]+v)
		{
			p=dep[to]+v;
			son[x]=to;
			dep[x]=p;
		}	 
	}
    for(int i=head[x];i;i=G[i].nxt)
	{
        int to=G[i].to;
        int v=G[i].v;
        if(to==f||to==son[x]) continue;
        dp[x]=max(dp[x],dep[x]+v+dep[to]);
    }
    dp[x]=max(dp[x],dep[x]);
    return;
}
int main()
{	
freopen("a.in","r",stdin); 
	scanf("%d",&n);
	int x,y,z;
	for(int i=1;i<n;i++)
	{
		scanf("%d%d%d",&x,&y,&z);
		add(x,y,z);add(y,x,z);
	}	
	dfs(1,0,0);
	t=s; int tmp=s;
	dfs(tmp,0,0);
	//直径计算完毕
	dfs1(s,0);
	for(int i=1;i<=n;i++)
	{
		dp1[i]=dp[i];
		dp[i]=dep[i]=0;
	}
	dfs1(t,0);
	x=s; int ans=1e9;
	while(x)
	{
		int to=fa[x];
		ans=min(ans,max(dp[x],dp1[to]));
		x=to;
	}
	printf("%lld\n",ans);
	return 0;
}