多目标进化算法基础知识整理

前言

特意整理一些多目标进化算法的基础知识点，尽量用通俗易懂的语言进行描述，希望对入门多目标算法的同学和对优化算法有兴趣的朋友有所帮助。

1.多目标优化细讲

使多个目标在给定区域同时尽可能最佳，多目标优化的解通常是一组均衡解（即一组由众多 Pareto最优解组成的最优解集合 ,集合中的各个元素称为 Pareto最优解），因此在多目标优化算法中，是对多个子目标的同时优化，而这些被同时优化的子目标之间往往又是相互冲突的，在解决多目标优化问题的时候，我们照顾了其中一个目标的"利益"，必然会导致其他至少一个子目标的”利益“受损，所以我们在面对一个多目标优化问题的时候 ，不会说找出一个唯一的最好的解。
在多目标优化算法中，对于不同的子目标函数可能会有不同的优化目标，一般有三种情况：
（1）最小化所有子目标函数
（2）最大化所有子目标函数
（3）最小化部分子目标函数，最大化其他子目标函数
一般情况下，统一为求总目标的最小化如下图例所示：

通常情况下，一般统一为求总目标的最小化。

2.pareto最优解

定义2.1：多目标优化问题中的最优解通常被称为pareto最优解。
定义2.2：多目标进化算法的优化过程，针对每一代进化群体，寻找出其当前最优个体（又称当前最优解），称一个进化群体的当前最优解为非支配解。（支配是多目标中非常重要的子目标与子目标之间的关系，它们存在支配和被支配的关系，可以形象理解为非支配解为老板，对其员工有支配的权力，是不会被员工支配的），所有的非支配解的集合称为当前群体的非支配集（后续非支配集会不断的逼近真正的最优解）。

3.pareto最优边界

定义3.1：pareto最优边界：是指一个多目标优化问题的pareto最优解在其目标函数空间中的表现形式。

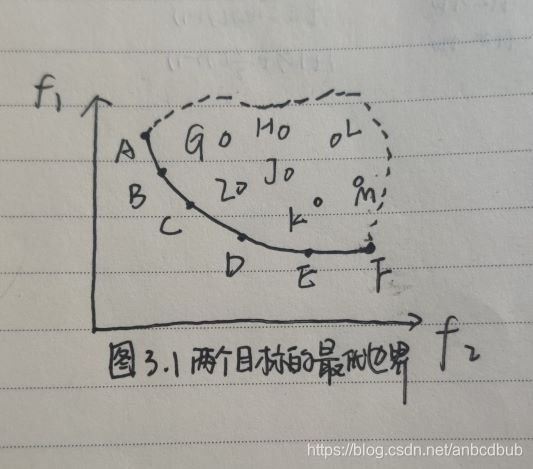
我们从上面的草图可以看到，那条实线段表示的是两个目标的最优边界（二维空间中，三维则会构成一个超平面），而点A B C D E F 均落在实线段上，所以是最优解，这里需要注意的一点是最优边界和最优解的区别和联系 ，pareto最优解集是决策空间的一个子集，而pareto最优边界是最优解集在目标函数空间的一个子集。
落在最优边界上的点实际上就是老板，它们是非支配的，其他点实际上相当于员工，不是最优解，是直接或间接被最优边界上的点支配的。

4.凹空间和凸空间

这两个概念算是很好理解的概念了，我们用一个定义就很容易理解，如定义4.1所示。
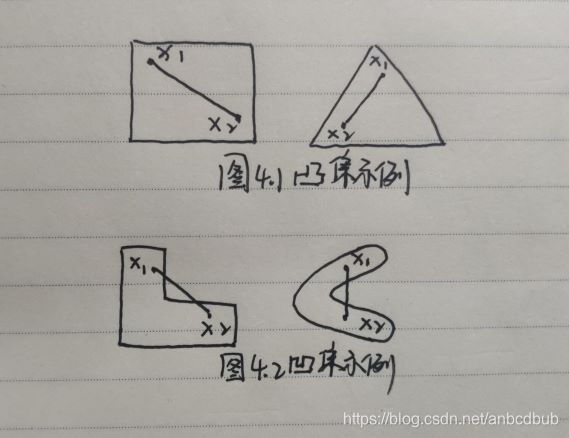
定义4.1：在一个集合中，任意两点的连线上的任意一点仍在该集合中，则该集合称为凸集，反之称为凹集；实例如下所示。

5.多目标进化个体之间的支配关系

举个例子：5和8；你能想到啥关系？人们通常有两种回答：（1）5小于8（2）5大于8
而在多目标的情况下，由于每个个体都有多个属性，个体和个体之间的属性又是不一样的，因此仅用大小关系来描述两个个体之间的关系是行不通的，比如说个体（2, 5)和个体（3，4），2小于3的同时5又 大于4，这两个个体如何确定它们之间的关系呢？
定义5.1 设p和q是进化种群P的任意两个个体，若p支配q则必须满足以下两个条件：
（1）对于所有的子目标，p不比q差，即fk（p)<=fk (q)，(其中k=1，2…r)。
（2）至少存在一个子目标，使p比q好。
称为p是非支配的，也就是不被支配的，而q则是被支配的。
例【1】：设一个二目标优化问题minf(X)={f1(X),f2(X),f3(X)},有三个可行解X1,X2,X3对应的目标向量值分别为：f1(X)=（3，8），f2(X)=（5，8）和f3(X)=（7，9）
根据定义5.1显然X1是支配X2和X3的 。