CCF认证 201803-4棋局评估——dfs+博弈

问题描述

问题描述

试题编号：	201803-4
试题名称：	棋局评估
时间限制：	1.0s
内存限制：	256.0MB
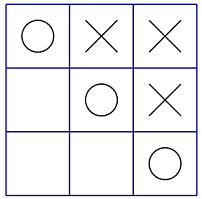
问题描述：	问题描述 　　Alice和Bob正在玩井字棋游戏。 　　井字棋游戏的规则很简单：两人轮流往3*3的棋盘中放棋子，Alice放的是“X”，Bob放的是“O”，Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时，游戏结束，该种棋子的持有者获胜。当棋盘被填满的时候，游戏结束，双方平手。 　　Alice设计了一种对棋局评分的方法： 　　- 对于Alice已经获胜的局面，评估得分为(棋盘上的空格子数+1)； 　　- 对于Bob已经获胜的局面，评估得分为 -(棋盘上的空格子数+1)； 　　- 对于平局的局面，评估得分为0； 　　例如上图中的局面，Alice已经获胜，同时棋盘上有2个空格，所以局面得分为2+1=3。 　　由于Alice并不喜欢计算，所以他请教擅长编程的你，如果两人都以最优策略行棋，那么当前局面的最终得分会是多少？ 输入格式 　　输入的第一行包含一个正整数T，表示数据的组数。 　　每组数据输入有3行，每行有3个整数，用空格分隔，分别表示棋盘每个格子的状态。0表示格子为空，1表示格子中为“X”，2表示格子中为“O”。保证不会出现其他状态。 　　保证输入的局面合法。(即保证输入的局面可以通过行棋到达，且保证没有双方同时获胜的情况) 　　保证输入的局面轮到Alice行棋。 输出格式 　　对于每组数据，输出一行一个整数，表示当前局面的得分。 样例输入 3 1 2 1 2 1 2 0 0 0 2 1 1 0 2 1 0 0 2 0 0 0 0 0 0 0 0 0 样例输出 3 -4 0 样例说明 　　第一组数据： 　　Alice将棋子放在左下角(或右下角)后，可以到达问题描述中的局面，得分为3。 　　3为Alice行棋后能到达的局面中得分的最大值。 　　第二组数据： 　　Bob已经获胜(如图)，此局面得分为-(3+1)=-4。 　　第三组数据： 　　井字棋中若双方都采用最优策略，游戏平局，最终得分为0。 数据规模和约定 　　对于所有评测用例，1 ≤ T ≤ 5。

解题思路:双方都按照最优策略走，找到非零值即可退出，此时空格数目最大，不需要再往下找，已经是最优值。满足胜的条件为

行、列或对角线，共八种情况

满分代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[4][4];
int block(){//空格的个数 
	int cnt=0;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			if(a[i][j]==0) cnt++;
		}
	}
	return cnt;
}
bool check_row(int row,int val){//检查行是否三个一样 
	if(a[row][0]==val&&a[row][0]==a[row][1]&&a[row][0]==a[row][2])
		return 1;
	return 0;
}
bool check_col(int col,int val){//检查行是否三个一样 
	if(a[0][col]==val&&a[0][col]==a[1][col]&&a[0][col]==a[2][col])
		return 1;
	return 0;
}
int win(int f){
	int wi=0,ans=1;//判断当前能否取胜
	if(check_row(0,f)||check_row(1,f)||check_row(2,f)) wi=1;
	if(check_col(0,f)||check_col(1,f)||check_col(2,f)) wi=1;
	if(a[0][0]==f&&a[0][0]==a[1][1]&&a[0][0]==a[2][2]) wi=1;
	if(a[0][2]==f&&a[0][2]==a[1][1]&&a[1][1]==a[2][0]) wi=1;
	if(wi==0) return 0;
	ans+=block();
	return (f==1)?ans:-ans;//alice赢为正数,bob赢为负数 
}
int dfs(int p){//搜索当前局面可能的走法的最大值 
	if(block()==0) return 0;//棋局已满
	int max_n=-10,min_n=10;
	for(int i=0;i<3;i++){
		for(int j=0;j<3;j++){
			if(!a[i][j]){
				a[i][j]=p+1;
				int w=win(p+1);
				if(w!=0){
					a[i][j]=0;
					return w>0?max(max_n,w):min(min_n,w);
				}
				if(!p) max_n=max(max_n,dfs(1));
				else min_n=min(min_n,dfs(0));
				a[i][j]=0;
			}
		}
	}
	return p==1?min_n:max_n;
}
int main(){
	int t;
	cin>>t;
	while(t--){
		for(int i=0;i<3;i++){
			for(int j=0;j<3;j++){
				cin>>a[i][j];
			}
		}
		int x=win(1),y=win(2);
		if(x){
			cout<<x<<endl;continue;
		}
		if(y){
			cout<<y<<endl;continue;
		}
		cout<<dfs(0)<<endl;//0为alice走,1为bob走 
	}
	return 0;
}