排序算法--归并排序--详解与代码

归并排序：

归并排序：（ Merge Sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（ Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并，使用中牺牲空间换取时间的算法

归并操作（ merge），也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法。

举例说明：

假如两个有序数列：（2，8，9，10）  （4，5，6，7）合成一个大数组arr[]就是（2，8，9，10，4，5，6，7）

可以看出它的左边是有序的，右边是有序的，但是整体是无序的

我们把左边的数组，和右边的数组拆除来

 

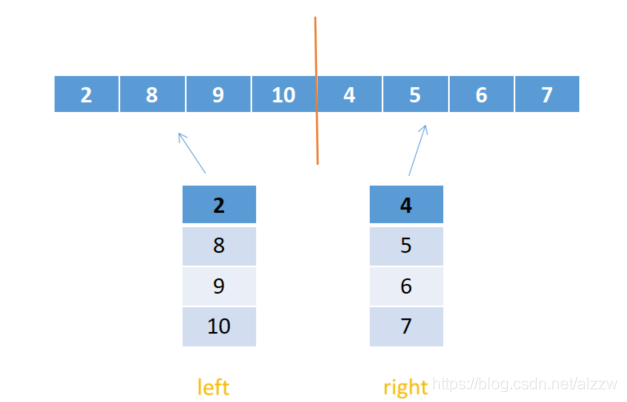
我们定义几个变量分别标记记录：

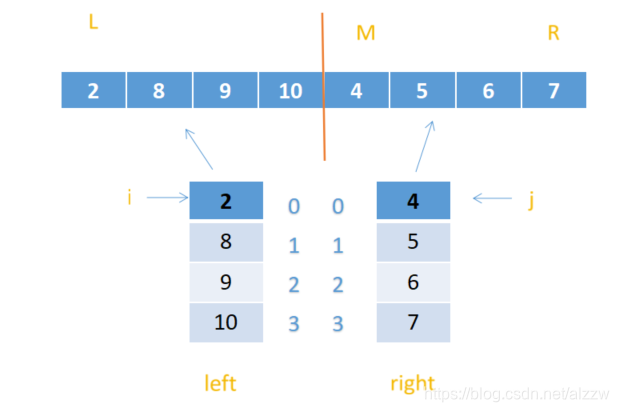
• L为原始数组最左边位置，所以数组left的长度为M-L
• R为原始数组最右边位置，数组right的长度为R-M+1
• M为中间位置

对于原始数组arr[]：

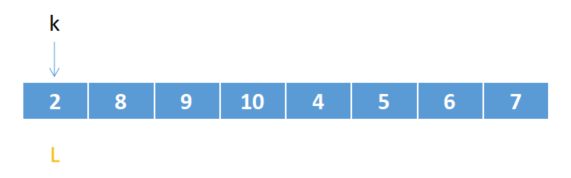
1.首先从i与j指向的值开始比较，比较i和j指向的值哪一个小,小的赋给arr【k】即left【i】<rigth【j】，所以arr【k】 = left【i】i++，k++；

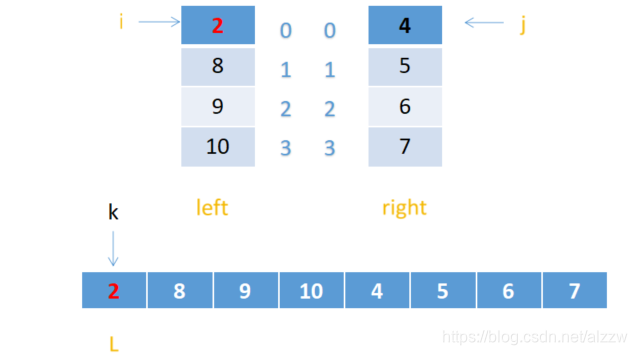
2.这时i指向8，j依然指向4，8>4，所以把4赋给arr【k】 j++，k++；

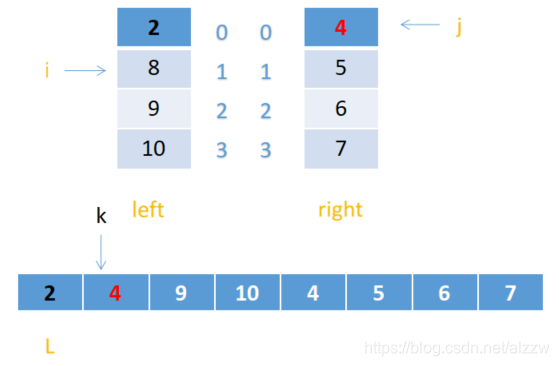
3.这时i指向8，j指向5，8>5,所以把5赋给arr【k】 J++，k++；

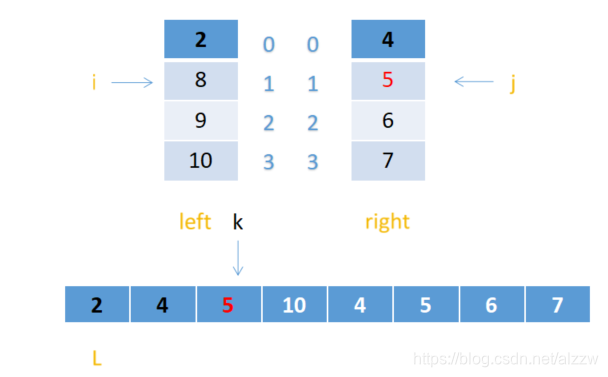
4.以此类推，当i和j不小于左右数组的长度时停止

 

如果：思考？

给定的数组两边不是有序的怎么办？

分治法把两边分别进行归并

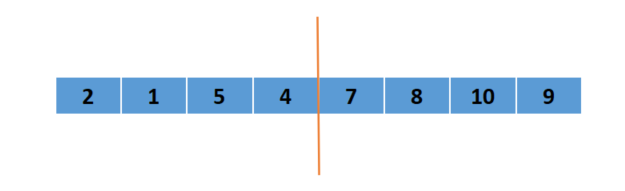
假如数组为：两边都不是有序的

一分为2：左右分别归并，如果不符合要求继续一分为二，直到两边只有一个数（一个数一定是有序的）

 

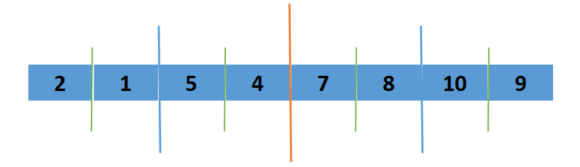
代码：

#include<iostream>
using namespace std;

void Merge(int* arr, int L, int M, int R)    //L，M，R分别为最左，中间，最右位置
{
	int left_size = M - L;                  //左边数组大小   
	int right_size = R - M + 1;              //右边数组大小
	int* L_arr = new int[left_size];           //左边数组
	int* R_arr = new int[right_size];            //右边数组

	for (int i = L; i < M; i++) {               //给左边数组赋值
		L_arr[i-L] = arr[i];
	}
	for (int i = M; i <= R; i++) {             //给右边数组赋值
		R_arr[i - M] = arr[i];
	}

	int i = 0, j = 0, k = L;
	while (i < left_size && j < right_size) {             //归并
		if (L_arr[i] < R_arr[j]) {
			arr[k++] = L_arr[i++];
			//k++;
			//i++;
		}
		else {
			arr[k++] = R_arr[j++];
			//k++;
			//j++;
		}
	}

	while (i < left_size){
		arr[k++] = L_arr[i++];
		//k++;
		//i++;
	}
	while (j < right_size) {
		arr[k++] = R_arr[j++];
		//k++;
		//j++;
	}
}

void Merge_Sort(int* arr, int left, int right)             //分治
{
	if (left == right)
		return;
	else {
		int M = (left + right) / 2;
		Merge_Sort(arr, left, M);
		Merge_Sort(arr, M + 1, right);
		Merge(arr, left, M+1, right);
	}
}

void Show(int* arr, int n)                 //输出
{ 
	for (int i = 0; i < n; i++)
		cout << arr[i] << ",";
	cout << endl;
}

int main()
{
	int arr[10] = { 6, 3, 2, 7, 5, 1, 4, 0, 8, 9 };
	Merge_Sort(arr, 0, 9);
	Show(arr, 10);
	return 0;
}

 

结果：

 

十大经典算法复杂度及稳定性比较：https://blog.youkuaiyun.com/alzzw/article/details/98100378

冒泡排序：https://blog.youkuaiyun.com/alzzw/article/details/97906690

选择排序：https://blog.youkuaiyun.com/alzzw/article/details/97964320

插入排序：https://blog.youkuaiyun.com/alzzw/article/details/97967278

快速排序：https://blog.youkuaiyun.com/alzzw/article/details/97970371

堆排序：https://blog.youkuaiyun.com/alzzw/article/details/98087519

基数排序：https://blog.youkuaiyun.com/alzzw/article/details/98240042

计数排序：https://blog.youkuaiyun.com/alzzw/article/details/98245871