2022.3.22 图论基础

---

文章参考自

前言：图可以玩出更多的算法，解决更复杂的问题，但本质上图可以认为是多叉树的延伸。面试笔试很少出现图相关的问题，就算有，大多也是简单的遍历问题，基本上可以完全照搬多叉树的遍历。

一、图的具体实现

图的实现方法①：逻辑上的实现

/* 图节点的逻辑结构 */
class Vertex {
    int id;
    Vertex[] neighbors;
}

类似多叉树节点

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

图本质上就是个高级点的多叉树，适用于树的 DFS/BFS 遍历算法，全部适用于图。

图的实现方法②：邻接表
实际使用中更常用的是邻接表

把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表关联起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;

图的实现方法③：邻接矩阵

邻接矩阵则是一个二维布尔数组，我们权且称为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][…] 就行了。

// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;

邻接表 VS 邻接矩阵：

邻接表，好处是占用的空间少。
邻接矩阵里面空着那么多位置，肯定需要更多的存储空间。

但是，邻接表无法快速判断两个节点是否相邻。
比如说我想判断节点 1 是否和节点 3 相邻，我要去邻接表里 1 对应的邻居列表里查找 3 是否存在。但对于邻接矩阵就简单了，只要看看 matrix[1][3] 就知道了，效率高。

所以说，使用哪一种方式实现图，要看具体情况。

二、图的遍历

遍历过程：

（我们需要引入两个数组，visited 数组用于处理图中的环，防止递归重复遍历同一个节点进入死循环；onPath 数组用于存储临时路径。
在 visited 中被标记为 true 的节点用灰色表示，在 onPath 中被标记为 true 的节点用绿色表示）

参考多叉树，多叉树的遍历框架如下：

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;

    for (TreeNode child : root.children) {
        traverse(child);
    }
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：

// 记录被遍历过的节点
boolean[] visited;
// 记录从起点到当前节点的路径
boolean[] onPath;

/* 图遍历框架 */
void traverse(Graph graph, int s) {
    if (visited[s]) return;
    // 经过节点 s，标记为已遍历
    visited[s] = true;
    // 做选择：标记节点 s 在路径上
    onPath[s] = true;
    for (int neighbor : graph.neighbors(s)) {
        traverse(graph, neighbor);
    }
    // 撤销选择：节点 s 离开路径
    onPath[s] = false;
}

三、例题

1.第八部分：图 – 797. 所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

答案代码：
graph 其实就是用「邻接表」表示的一幅图，graph[i] 存储节点 i 的所有邻居节点。

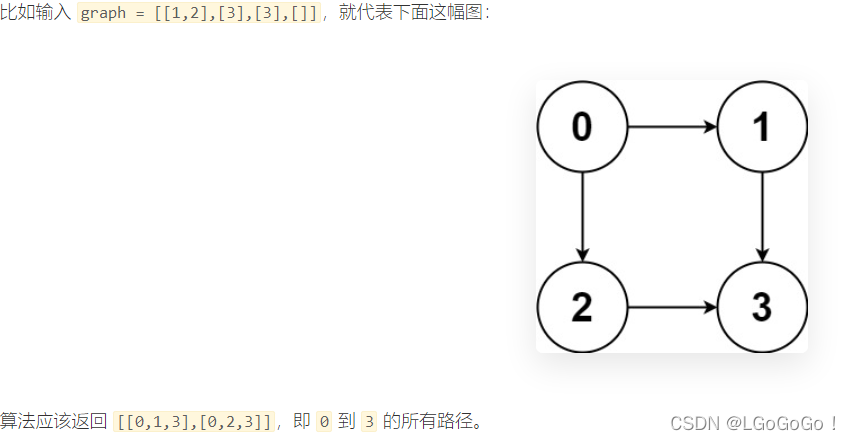
本题的遍历思想本质上是以 0 为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。

package Graph;

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;

/**
 * @author: LYZ
 * @date: 2022/3/22 12:14
 * @description: 797. 所有可能的路径
 */
public class AllPathsSourceTarget {
    public static void main(String[] args) {
        int[][] graph = {{1,2},{3},{3},{}};
        AllPathsSourceTarget all = new AllPathsSourceTarget();
        List<List<Integer>> ans = all.allPathsSourceTarget(graph);
        for (List<Integer> list : ans) {
            System.out.println(list);
        }
    }

    // 记录所有路径
    List<List<Integer>> res = new LinkedList<>();

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        // 维护递归过程中经过的路径
        LinkedList<Integer> path = new LinkedList<>();
        traverse(graph, 0, path);
        return res;
    }

    /* 图的遍历框架 */
    void traverse(int[][] graph, int s, LinkedList<Integer> path) {
        // 添加节点 s 到路径
        path.addLast(s);

        int n = graph.length;
        if (s == n - 1) {
            // 到达终点
            res.add(new LinkedList<>(path));
            path.removeLast();
            return;
        }

        // 递归每个相邻节点
        for (int v : graph[s]) {
            traverse(graph, v, path);
        }

        // 从路径移出节点 s
        path.removeLast();
    }
}

四、二维数组的声明：

参考自

四种方式：

1.

类型 数组名[][ ]={{初始值1}，{初始值2}，{初始值3}};

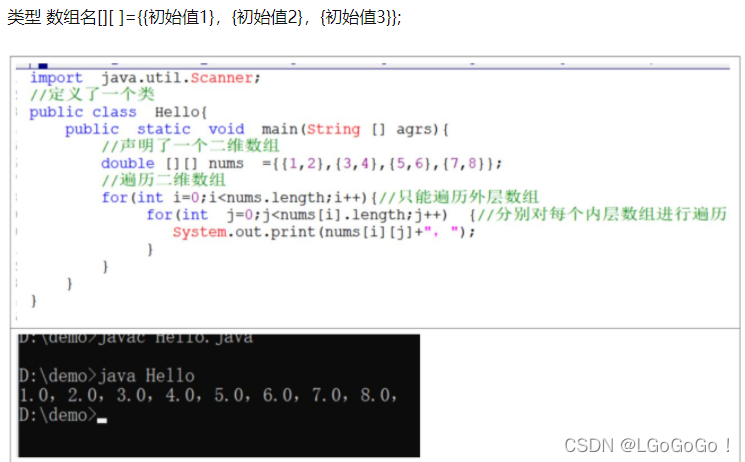
2.

类型 数组名[][ ]=new 类型[长度][长度];

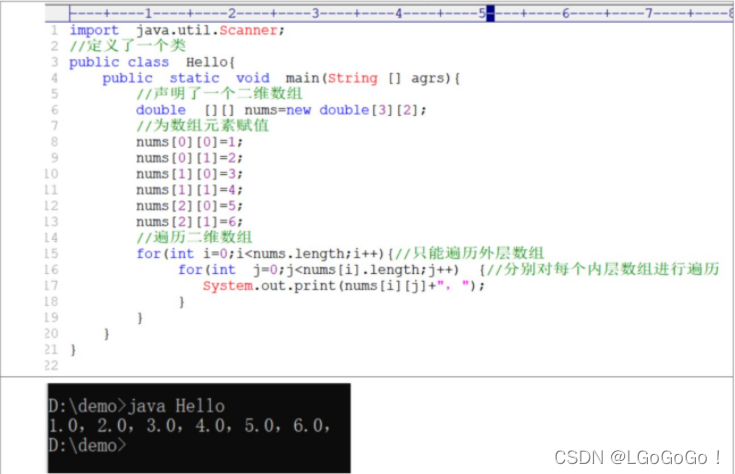
3.

类型 数组名[][ ]=new 类型[长度][];

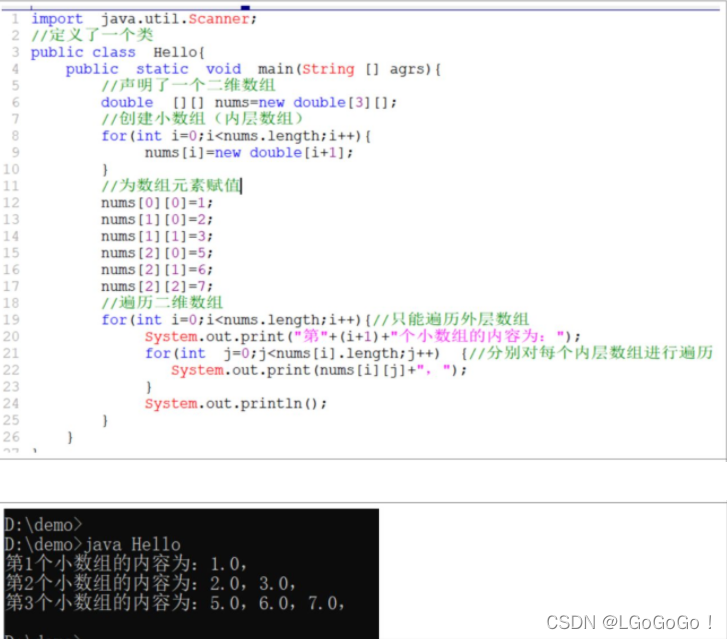
4.

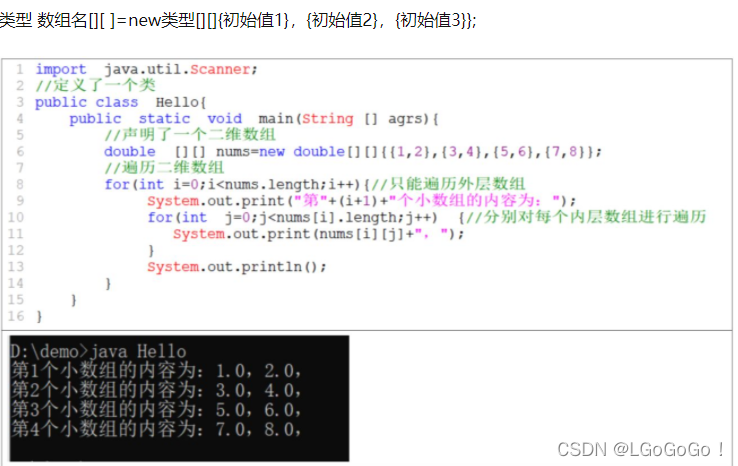
类型 数组名[][ ]=new类型[][]{初始值1}，{初始值2}，{初始值3}};